§ 4. Метод оценки. Теоретические результаты эксперимента с использованием метода оценки

§ 4. Метод оценки

Этот метод может быть использован как модификация метода " Да-Нет" и как модификация метода 2АВВ. Здесь будет изложен только первый вариант, поскольку перенесение его на случай 2АВВ является тривиальным.

Как мы уже знаем, в ряде случаев (для проверки гипотез о форме распределений или для вычисления таких мер чувствительности, как U) требуется РХ по достаточно большому количеству точек. Для получения нескольких точек РХ методом " Да-Нет" необходимо несколько раз провести эксперимент с одной и той же парой < S> и < N>, но с различными параметрами организации эксперимента, такими как P(S), платежная матрица и т. п. Каждый эксперимент должен содержать большое количество предъявлений для того, чтобы, во-первых, можно было исключить первые пробы, в которых схема соответствия еще не установилась, и, во-вторых, чтобы частоты событий (" Да" /S) и (" Да" /N), высчитанные по оставшимся пробам (асимптотический уровень), достаточно точно соответствовали вероятностям р(Н) и p(FA). Более того, поскольку от эксперимента к эксперименту чувствительность наблюдателя к данному сигналу может меняться, эксперимент с одними и теми же параметрами организации желательно повторить несколько раз на разных этапах (скажем, ближе к началу, середине и концу) всей серии экспериментов. Все это довольно громоздкая работа. Метод оценки (МО) дает нам возможность получить несколько точек РХ в результате только одного эксперимента, хотя его объем, обыкновенно, превышает объем одного эксперимента " Да-Нет".

Процедура метода оценки (МО) отличается от метода " Да-Нет" только тем, что после каждого предъявления вместо ответа " Да" или " Нет" испытуемый указывает степень его уверенности в наличии/отсутствии сигнала в этом предъявлении. Например, " совершенно уверен, что сигнал был", " уверен, что сигнал был", " скорее был, чем не был", " не могу выбрать", " скорее не был, чем был", " уверен, что сигнала не было", " совершенно уверен, что сигнала не было". Эти 7 категорий естественно обозначить числами в том же порядке: 3, 2, 1, 0, -1, -2, -3. В методе оценки уверенности набор категорий всегда задается испытуемому заранее и обычно кодируется некоторой числовой системой. Иногда используется процентная шкала, когда испытуемый говорит о сигнале: " На 50% был", " На 100% был" (точно был), " На 10% был", " На 0% был" (точно не был). В этом случае либо испытуемого просят пользоваться только определенными (например, только круглыми: 0, 10, 20... %) числами, либо он может называть произвольные проценты (скажем, 78%), но потом ответы объединяются в несколько групп (например, все числа меньше 5% — в группу 0, все числа между 5 и 15 — в группу 10% и т. д. ). Для конкретности предположим, что испытуемому заданы 7 категорий, названных в нашем примере. Обыкновенно эксперимент проводится без платежной матрицы или с симметричной платежной матрицей и с P(S) = Р(М) = 0. 5. Результаты эксперимента могут быть представлены в виде следующей таблицы (см. табл. 5).

Таблица 5

Теоретические результаты эксперимента с использованием метода оценки

Р(n), n = -3,... +3, есть оценка условной вероятности P(n/S), получаемая путем деления числа всех случаев, когда предъявлялось < S> и был дан ответ " n", на число всех предъявлений < S>. Аналогично q(n) есть оценка условной вероятности P(n/N). Теоретическое осмысление этих данных в рамках модели, изложенной в двух предыдущих разделах, состоит в предположении, что если испытуемому заданы К категорий (от полной уверенности в отсутствии до полной уверенности в наличии S), то он так же, как и в условиях эксперимента " Да-Нет", базируется на интенсивности некоторого сенсорного качества, но делит ее не на две, а на К областей, как показано на рис. 17.

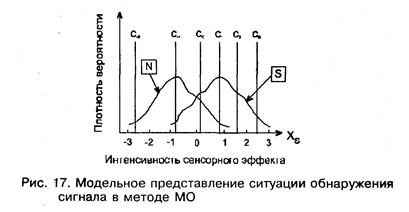
Как видим, совсем необязательно, чтобы границы между областями разных ответов следовали через равные интервалы или каким-нибудь закономерным образом: единственное, что предполагается — что область ответа R₁ лежит левее области ответа R₂ если С₁ < С₂. Итак, если выбранное качество сенсорного образа имеет интенсивность, лежащую между С₀ и С₁ то испытуемый дает ответ " 0", если интенсивность лежит правее С₃ — то " 3" и т. д.

Теперь приведем следующее рассуждение. Допустим, что те же стимулы < N> и < S> используются в эксперименте " Да-Нет", причем критерий С будет последовательно помещаться в позиции С₃, С₂, С₁, С₀, С_-1, С_-2. При каждом положении критерия будем вычислять соответствующую пару р(Н) и p(FA). Вероятность р(Н) равна площади под кривой f(X/S), лежащей правее С, a p(FA) равна площади под кривой f(X/N), лежащей правее С. Обозначим площадь под кривой f(x/S) между С_i и С_i+1 (i = -2, -1... 2 в нашем случае на рис. 17) через A_s (С_i, C_i+1), а площадь, лежащую правее C_i -через А_s (С_i, C_∞ ). Для кривой f(X/N) — аналогичные обозначения: A_N (С_i, С_i+1) и А_N (С_i, С_∞ ). Если критерий С помещен в позицию С_i, то р(Н) = А_s (С_i, C_∞ ), p(FA) = A_N (С_i, С_∞ ). С другой стороны, ясно, что p(i) - вероятность ответа «i» при предъявлении S, равна A_s (С_i, С_i+1), если i < 3 и равна A_s (С₃, C_∞ ), если i = 3. Аналогично q_i = A_N (C_i, C_i+1), если i < 3 и A_N (С₃, C_∞ ), если если i = 3. Но, очевидно, что, A_s (С₀, C_∞ ) = А_s (C₀, С₁) + А_s (С₁, С₂) + А_s (С₂, C₃) + A_s (С₃, C_∞ ), и аналогично раскладываются любые другие А_s (С₁, C_∞ ) и A_N (С_i, C_∞ ). Следовательно, мы получаем следующую цепочку равенств (табл. 6):

Таблица 6