 |
§ 4. Процедура решения V варианта закона сравнительных оценок для полной матрицы
|
|
|
|
§ 4. Процедура решения V варианта закона сравнительных оценок для полной матрицы
В V варианте закона, записанном в общем виде (9), единицы измерения шкальных значений всегда можно подобрать так, чтобы константа " с" была равна 1. Тогда:

В случае отсутствия ошибок в оценках искомое различие будет равно наблюдаемому (обозначим его z'j, i). Но в результате ошибок между z'j, i и z. j, i будет некоторое расхождение σ. Задача заключается в получении такого множества оценок шкальных значений стимулов, для которых сумма квадратов всех расхождений является минимальной, т. е. необходимо минимизировать величину
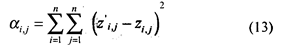
Подставив вместо zi, j идеальные значения, получим:
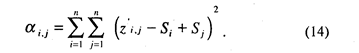
Все аi, j для всех zi, j из матрицы Z дадут матрицу ошибок α.. Чтобы минимизировать каждую α i, j, необходимо взять частную производную α i, j по Si и Sj. Каждое частное значение Si в матрице ошибок а появляется только в i-той строке и i-том столбце, но поскольку матрица ошибок так же кососимметрична [zi, j = -zj, i и (Si - Sj) = - (Sj - Si)], как и матрицаZ, то для каждой Si частная производная будет касаться только i-гo столбца. Дифференцируя элементы каждого столбца по Si, получим:

Приравняем частную производную нулю и после переноса получим:

Разделим выражение (16) на n и возьмем начальное значение шкалы, равное  . В результате получим:
. В результате получим:

Таким образом, для минимизации ошибки необходимо просто взятъ среднее арифметическое по столбцу матрицы Z и мы получим оптимальное значение шкальной величины Si.
Рассмотрим практический пример решения V варианта закона сравнительных оценок методом наименьших квадратов (данные вымышлены). Испытуемому в случайном порядке предъявляются 6 цветных карт из малого набора теста Люшера и просят в каждой паре выбрать наиболее красивый. Каждая пара предъявляется по 50 раз. В итоге для одного из испытуемых была получена следующая матрица частот F (табл. 1):
|
|
|
Таблица 1
Матрица частот — F

Примечание: элементом матрицы fi, j является частота, с которой в паре j, i стимул i оценивался более красивым, чем стимул j.
Полученная матрица частот F преобразуется в матрицу вероятностей Р делением частоты fi, j на число предъявлений (N = 50).
Таблица 2
Матрица вероятностей Р

Примечания: элементом матрицы рi, j является вероятность, с которой стимул i в паре j, i оценивался более красивым, чем стимул j.
Каждое значение вероятности рi, j из матрицы Р переводится далее с помощью таблицы в единицы стандартного отклонения нормальной кривой — zi, j, по которым и вычисляются шкальные значения Si каждого стимула.
Таблица 3
Матрица Z - оценок
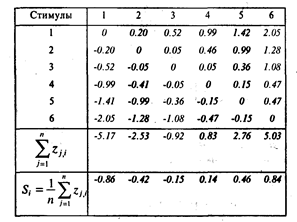
Примечания: элементом матрицы zi, j является вероятность рj, i, преобразованная в единицы стандартного отклонения.
Рассмотренная процедура дает возможность для каждого стимула Si получить его значение на шкале интервалов.
§5. Процедура решения V варианта закона сравнительных суждений для неполной матрицы исходных данных
Реальные экспериментальные данные очень часто отличаются от той классической матрицы данных, которая анализировалась выше. Наиболее распространенный артефакт в процедуре парного сравнения, который связан с ограничением на возможное число предъявлений, — стопроцентное предпочтение одного стимула другому, что приводит к появлению в матрице вероятностей нулей и единиц. Ноль и единица в терминах модели Терстоуна не несут сравнительной информации о различии стимулов, поэтому не могут быть использованы для расчетов шкальных значений стимулов.
|
|
|
Для матриц с нулями и единицами (они называются неполными матрицами) существуют особые алгоритмы анализа. Наиболее распространенный из них подробно описан в работе Торгерсона (1958) и вкратце состоит в следующем.
Из выражения (12) для стимула j следует, что стимул j+1 будет описываться следующим выражением:

Вычтя из уравнения (18) уравнение (12), мы получим сравнительное различие для интересующего нас стимула косвенным путем. В терминах минимизированной ошибки эта величина может быть вычислена из выражения:
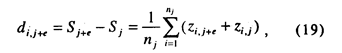
где nj — есть индекс суммирования.
Для практического удобства матрицу Z следует перестроить таким образом, чтобы столбцы были упорядочены по величине. Порядок столбцов в матрице Z определяется суммой по столбцу матрицы Р. Для такой упорядоченной матрицы Z различие Sj+e - S, можно прямо вычислить из выражения (19). Если мы шкальное значение первого стимула (S; ) приравняем к нулю, то шкальное значение любого стимула есть сумма шкального значения стимула и расстояния между данным стимулом и предшествующим:

Рассмотрим практический пример решения для неполной матрицы частот, взятый из работы Торгерсона (1958). Пусть нам дана матрица вероятностей предпочтения i-го стимула j-му с некоторыми вырожденными (пустыми) элементами, равными 0 или 1.
Таблица 4
|
|
|


