Результаты оценки испытуемыми стимула как половины стандартного (по Харперу и Стивенсу, 1948)

 

4. Построение графика деления (умножения) на п и психофизической функции. Средняя оценка стимулов, находящихся в заданном отношении п со стандартом, вычисляется либо как медиана Md, которая является грубой, но просто вычисляемой оценкой, либо как среднее геометрическое G, определяемое по формуле:

 

 

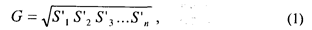
где, S₁... S_n — величины стимулов, оцененных как составляющие заданную часть от стандартного; n — число повторных оценок.

Если число оценок больше трех, то G удобнее находить путем логарифмирования:

 

 

Харпер и Стивенc воспользовались, как уже было сказано выше, медианой для оценки весов, воспринимаемых как половина стандартного. На основании полученных данных была определена зависимость S' = f(S_st), где S' — медиана стимулов, оцениваемых как половина стандартного стимула. Эта зависимость представлена на рис. 1.

 

 

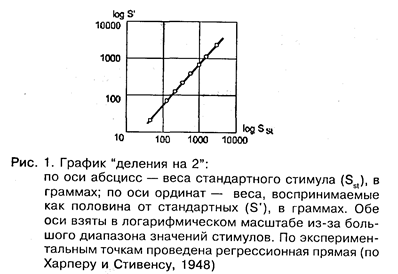
В данном случае экспериментальные точки почти точно ложатся на прямую, и она без явных ошибок может быть проведена на глазок.

Обычно линия, сопоставляющая на графике деления на п каждому стандартному стимулу S_st стимул S', воспринимаемый как объективно в п раз меньший, проводится через конечное и, как правило, небольшое число точек, соответствующих использованным стандартным стимулам. Проведение плавной линии через несколько точек, разумеется, всегда содержит ошибку, неточность. Однако, если вид зависимости известен (линейная, логарифмическая и т. п. ), то неточность по отношению к экспериментальным точкам можно минимизировать. Минимизация ошибки является задачей регрессионного анализа, а полученная в результате решения этой задачи линия называется линией регрессии (прямолинейной, логарифмической и т. п. ). Пока мы можем забыть о допускаемой неточности в определении этой кривой и рассматривать ее как непрерывную и " точную" для всех S.

Как от графика деления на п, который является только стимульно-стимульной функцией, перейти к психофизической функции? Для этого нужно только ввести единицу измерения на субъективной шкале, поскольку все нужные для построения субъективной шкалы соотношения субъективных и стимульных значений уже содержатся в полученной в опыте зависимости: S' = f(S_st). Для этого выбирается какой-либо из стандартных стимулов и соответствующее ему значение на шкале ощущения (Z) принимается за единицу (Z = l). Харпер и Стивенc выбрали в качестве такового ощущение тяжести, возникающее при поднятии груза 100 г., и назвали эту единицу " вег" (от старонорвежского слова, имеющего значение " поднимать" ). Естественно, что шкальное значение того веса, который испытуемый оценил как вдвое менее тяжелый, чем S_st = 100 г, равно 1/2 вега. Это вес 77 г. В принципе метод установления заданного отношения позволяет указать любой стимул, которому соответствует шкальное значение, равное n^a, где а = 0, ±1, ±2.... В нашем примере, где 1/n = 1/2, можно найти значения 1/4, 1/8, 1/16, 2, 4, 8, 16 и т. д. Как это делается показание на рис. 2.

 

 

Примем, что шкальное значение, соответствующее стимулу S₁, равно 1. Таким образом, мы вводим единицу измерения на будущей шкале (в нашем примере — это 1 " вег" ) и строим на ней первую точку с координатами (100; 1 или S₁; S'₁ нa рис. 2). Тогда стимулу S₀, оцененному как в n раз меньший, соответствует шкальное значение 1/n. Отложив по оси абсцисс значение S₀ (мы его находим без труда из графика " деления на n", приведенного на рис. 1, т. к. в опыте уже найден тот вес, который ощущается как половина от S₁), соотносим его со шкальным значением 1/n и строим на графике вторую точку. В нашем примере шкальное значение S'₀ будет равно 1/2. Так можно найти и все дальнейшие отрицательные степени n. Естественно, что точность построения психофизической функции будет зависеть от точности вычислений стимульных значений по графику " деления на n", что, в свою очередь, определяется " хорошестью" подгонки экспериментальных точек под плавную кривую или прямую, отражающую устойчивость полученной эмпирической зависимости. Чтобы получить все положительные степени того же отношения, необходимо изменить направление наших расчетов. Найдем по графику " деления на n" величину стимула, который при делении на n дает 1 вег — S'₂. Эту величину можно найти, проведя перпендикуляр от той точки на оси ординат, которая соответствует 1 вегу, до пресечения с аппроксимирующей кривой (прямой), и из точки пересечения опустить перпендикуляр на абсциссу. Найденная величина (S₂) соответствует n вегам (в нашем примере n = 2) и может, в свою очередь, быть использована для определения 2n вегов и т. д.

По найденным парам значений на субъективной шкале (Z) и на физической шкале стимулов (S) строится психофизическая функция: по оси абсцисс откладываются субъективные величины (например, веги), а по оси ординат — соответствующие им значения физического параметра стимула (например, граммы). Плавная линия, соединяющая точки, образованные парами значений Z и S, и образует графическую шкалу ощущений тяжести. Эта линия может быть проведена " на глазок" или с использованием методов регрессионного анализа и аппроксимирована подходящей математической функцией.

В дальнейшем психофизическая зависимость может использоваться для определения шкальных значений любого стимула, в том числе и такого, который не применяется в опыте, например, лежащего между S’₁ и S’₂. В самом деле, такому стимулу нельзя приписать однозначно шкальное значение, поскольку к нему нельзя " прийти" от предъявлявшихся в эксперименте стимулов S₁ или S₂ путем описанной выше процедуры с помощью кривой " деления на n". Можно только утверждать, что его шкальное значение лежит между 1/n и 1. Это утверждение будет справедливо лишь при допущении, что психофизическая зависимость является строго монотонной. Неточность в определении шкального значения, соответствующего этому стимулу, возрастает за счет ошибки при построении психофизической зависимости.

Психофизическая функция, построенная по данным Харпера и Стивенса показана на рис. 3.

Аналитический способ, который дает более точное определение субъективной шкалы, поскольку лишен ошибок, связанных с неточностью проведения графических работ, подробно описан Гилфордом (1954). Здесь приведем только краткую схему аналитического решения, поскольку для тех, кто владеет минимальными навыками регрессионного анализа, с помощью любой современной статистической программы оно не представляет большого труда*. Подобранные в опыте значения стимулов, оцененных как в п раз меньшие (большие), чем стандартные, преобразуются в логарифмы и с помощью метода наименьших квадратов определяется уравнение прямой. Качество подгонки полученной прямой под экспериментальные точки оценивается стандартным образом. Используя это уравнение, можно вычислить любое значение на оси " X" по известному значению на оси " Y" (и наоборот). Естественно, что точность получаемых оценок будет зависеть от качества полученной регрессионной прямой. Находя таким образом нужные значения на оси " X" конструируемой психофизической функции, получают все необходимые точки. После этого, применяя методы регрессионного анализа, определяют вид функции, описывающей психофизическую зависимость. Поскольку психофизические функции, как правило, нелинейны, удобнее представлять результаты на графике и проводить регрессионный анализ в логарифмическом масштабе по оси абсцисс. Если эта функция подчиняется закону Фехнера, то в этом случае она будет прямой. Если же психофизическая функция степенная, то представление ее в виде прямой можно получить только в двойных логарифмических координатах (так называемые log-log-координаты), т. е. введя логарифмический масштаб также и по оси ординат. Таким образом, изображение психофизической функции в виде прямой в логарифмических координатах, является своеобразным " тестом" на ее соответствие одному из основных психофизических законов.

* Конкретные методические рекомендации о том, как выполнить эту процедуру с помощью статистической системы " Stadia", будут даны ниже при описании учебного задания.

 

5. Проверка соответствия процедуры шкалирования шкале отношений: деление (умножение) на два взаимно простых числа.

Судя по приведенному выше описанию, метод фракционирования довольно груб с точки зрения получения точной психофизической зависимости. Оказывается, однако, что это не единственный и даже не самый главный его недостаток. Дело в том, что процедура этого метода не содержит возможности проверить, существует ли соответствие между выполненными испытуемым операциями отыскания стимула, относящегося как 1/п к стандартному, и свойствами шкалы отношений. Следовательно, мы имеем повод сомневаться в том, действительно ли можно строить шкалу отношений по кривой деления (умножения) на п.

Проверка выполнения свойств шкалы отношений. Уточним, что следует понимать под " соответствием операций свойствам шкалы". В данном случае соответствие означает, что операция деления (умножения) стимула на число п (т. е. отыскания стимула, составляющего субъективно 1/n-ю от стандарта) эквивалентна математической операции деления (умножения) наименованного числа (значения предполагаемой шкалы) на число-скаляр п. " Эквивалентна" означает, что она обладает теми же свойствами. Названная математическая операция обладает свойствами ассоциативности, коммуникативности, тотальной сравнимости, обратимости и неизменности при умножении на 1. Для наших целей достаточно представить эти свойства в виде следующих правил:

1. Z = Z ∙ 1 для любого шкального значения Z.

2. Z ∙ α ₁ ∙ α ₂ ∙ α ₃ ∙ … ∙ α _n = Z ∙ β ₁ ∙ β ₂ ∙ β ₃ ∙ … ∙ β _n, если и только если α ₁ ∙ α ₂ ∙ α ₃ ∙ … ∙ α _n = b₁ ∙ b₂ ∙ b₃ ∙ ... ∙ b_n (это правило включает в себя и коммуникативность, и ассоциативность).

3. Для любых двух Z₁ и Z₂ существует единственное α, такое, что Z₁ = Z₂ ∙ α . (тотальная сравнимость).

4. Если Z₁ = Z₂ ∙ α, то Z₂ = Z₁ ∙ 1/α (это свойство обратимости)*.

* Это правило формально выводимо из правила 2, но для удобства его выделяют отдельно.

 

Рассмотрим, что означают эти правила на языке эмпирических операций деления (умножения):

1. Свойство 1 выполняется очевидно всегда, если только нет систематических ошибок, связанных с условиями эксперимента.

2. Пусть испытуемый " делит" стимул S на 2, тем самым он выбирает новый стимул S’₁. Стимул S’₁ он " делит" на 3 — выбирает стимул S'₂. Если бы первое " деление" было не на 2, а на 3, то вместо S'₁ должен был бы выбираться некоторый стимул S''₁. Правило 2 гарантирует, что если теперь S" ₁ " разделить" на 2, то получится опять S'₂ (т. к. 1/3 ∙ 1/2 = 1/2 ∙ 1/3). Этот пример, а также и другие примеры, демонстрирующие проверку правила 2, приведены на рис. 4.

 

 

 

3. Правило 3 означает, что путем каких-то " умножений" и " делений" от одного стимула всегда можно " добраться" до любого другого. Если эксперимент организован так, что это правило выполняется, то мы избавляемся от необходимости строить психофизическую зависимость приблизительно (ведь до любого стимула можно " добраться" от " единичного" и тем самым получить точно соответствующее ему шкальное значение).

Можно доказать следующее утверждение: если экспериментально построены не одна кривая " деления на n" (см. рис. 1), а две — " деления на m" и " деления на n", где n и m — взаимно простые числа (например, 2 и 3), то правило 3 выполняется. Доказательство следует из того факта, что любое шкальное значение может быть сколько угодно точно приближено числом вида 2^a ∙ 3^b (а, b = 0, ±1, ±2,... ).

4. Правило 4 поясняется на рис. 5.

 

 

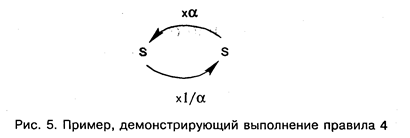
Здесь, как и на рис. 4, стрелка обозначает выбор нового стимула. Проверка выполнимости правила может быть осуществлена так: строится кривая " деления на n" и кривая " умножения на n", они должны совпасть с точностью до перемены осей (как функции ln и ехр).

6. Определение вида психофизической зависимости.

Если бы возможный вид зависимости был совсем неизвестен, пришлось бы проделывать большую работу: провести регрессионный анализ для опытных данных, проверить выполнение свойств шкалы отношений, построить кривую психофизической зависимости и только после этого можно подбирать математическое выражение для полученной психофизической функции. Положение облегчается, если вид психофизической зависимости известен или по крайней мере должен быть осуществлен выбор между несколькими известными видами.

Известно, что большинство психофизических зависимостей может быть представлено в степенной или логарифмической форме. Рассмотрим основные варианты этих форм и те следствия, которые из них вытекают для кривых " деления" и " умножения". Все эти следствия (хотя это и не будет доказываться) на самом деле являются не только необходимыми, но и достаточными условиями выполнения соответствующих форм психофизической зависимости.

1. Простейшая степенная форма Z = aS^α . Какой вид должна иметь кривая " умножения" на n? Чтобы выяснить это, рассмотрим два значения стимула S и S_n, такие, что соответствующие им ощущения относятся как Z и Z ∙ n:

 

 

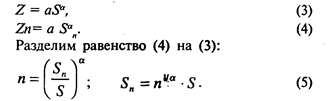
Таким образом, если построить прямую наилучшего приближения по данным " умножения на n" (стимульно-стимульная кривая, где по оси абсцисс отложены значения стандартного стимула S, а по оси ординат — стимула, субъективно в n раз большего S', см. рис. 6), то:

1) прямая пройдет через начало координат (0, 0);

2) наклон прямой покажет показатель степени в законе Стивенса. Этот показатель мы получим, если возьмем логарифм тангенса наклона (при основании, равном коэффициенту " умножения/деления" n), т. е. log_ntgφ ), и вычислим обратную этому выражению величину (см. рис. 6).

2. Степенная форма Z = k(S – S₀)^α является степенной зависимостью с " порогом" (при S = S₀ ощущение равно 0, т. е. исчезает). Значения S < S₀ не рассматриваются. По аналогии с (3) и (4) запишем:

 

 

Разделив второе равенство на первое и проведя элементарные преобразования, получим:

 

 

Итак, линия " умножения на n" оказывается прямой с наклоном n, но не проходит через начало координат (см. рис. 7).

 

 

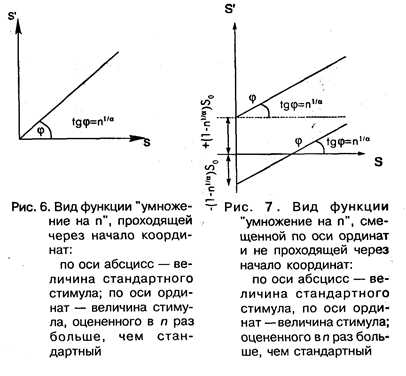
Построив прямую наилучшего приближения по данным " умножения на n", вычислим аналогично тому, как это делалось в предыдущем пункте А, показатель степени Стивенса. Однако, непрохождение прямой через (0, 0) не позволяет ограничиться проделанным: недостаточно знать только α, нужно еще вычислить S₀. Прямая " умножения на n" пересекает ось ординат на уровне (1 – n^1/α )S₀. Разделив эту величину на (1 - n^1/α ), получим S₀.

На рис. 6 и 7 изображена прямая " умножения на n" в предположении, что Z = aS^α (рис. 6) и в предположении, что Z = k(S_n – S₀)^α (рис. 7). На рис. 7 также показан случай, когда (1 – n^1/α )S₀ — величина отрицательная. Если S действительно является " порогом", то независимо от знака этой величины S₀ должна быть величиной положительной. Если этого не произойдет, то интерпретация S₀ меняется. Функция Z = k(S + r)^α (где r > 0) показывает наличие " шума", так что и при нулевом стимуле S₀ имеет место ненулевое ощущение Z = kr^α . Эта разница в интерпретации не влияет на формальный анализ.

3. Простейшая логарифмическая зависимость Z = logS. В этом случае пара равенств, задающих кривую " умножения на n" такова:

Z = log S,                             (3')

Z=log S_n.                               (4')

 

Очевидно, что, проведя те же вычисления, как и в предыдущих пунктах, мы получим:

logS_n = n logS,                      (5')

 

т. е. определенно нелинейную зависимость. Значит, если мы ожидаем логарифмическую, а не степенную зависимость, не следует строить прямых наилучшего приближения.

Если мы все же их построим, то они окажутся " плохими" в смысле приближения к опытным точкам, и самое главное, вычисления по разным n (n = 1/2, 1/3 и 2) дадут нам разные величины а. Выход из затруднения состоит в том, что данные " умножения на n" следует откладывать в двойных логарифмических координатах. Тогда, согласно (2" ), наилучшим приближением будет прямая, наклон которой равен коэффициенту фракционирования n (см. рис. 8).

 

 

4. Логарифмическая форма Z = logS + b. В этом случае имеем:

 

Z = logS + b,                         (3" )

Zn = logS_n + b.                     (4" )

 

Поделив второе равенство на первое и произведя элементарные преобразования, получим:

 

logS_n = n logS +(n - l)b.          (5" )

 

График этой зависимости в двойных логарифмических координатах показан на рис. 9.

 

⇐ Предыдущая26272829303132333435Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: