Законы распределения и числовые характеристики случайных векторов.

Пусть для данного эксперимента определены случайные величины . Каждому элементарному событию ω можно поставить в соответствие п-мерный случайный вектор (п-мерную случайную величину)

задающий отображение .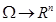

Функцией распределения n-мерного случайного вектора или функцией совместного распределения случайных величин X₁, Х₂,..., Х_п называется неслучайная функция п действительных переменных , определяемая как вероятность совместного выполнения п неравенств

(3.1)

В частном случае, для двумерного случайного вектора (X, У), имеем по определению

(3.2)

Функция распределения обладает следующими свойствами:

1.

2.

3.

4. Функция — неубывающая функция своих аргументов.

5. Функция непрерывна слева по каждому из аргументов.

Свойство 2 обычно называют условием согласованности. Оно означает, что функции распределения отдельных компонент двумерного случайного вектора могут быть найдены предельным переходом из функции совместного распределения этих компонент.

Вероятность попадания случайной точки на плоскость (X, Y) в прямоугольник со сторонами, параллельными осям координат, может быть вычислена с помощью функции распределения по формуле

(3.3)

 

Двумерный случайный вектор (X, У) называется дискретным случайным вектором (ДСВ), если множество его возможных значений не более чем счетно.

Перечень возможных значений пар компонент и соответствующих каждой такой паре вероятностей , удовлетворяющих условию

(3.4)

где суммирование распространяется на все возможные значения индексов и , называется законом распределения ДСВ. Закон распределения двумерной случайной величины часто задаётся в виде таблицы (матрицы) распределения:

 

Одномерные законы распределения отдельных компонент ДСВ выражаются через вероятности совместных значений , по формулам

(3.5)

где суммирование распространяется на все возможные значения индексов i или j.

Пусть (X, У) — двумерный дискретный случайный вектор, — множество его возможных значений. Условным законом распределения случайной компоненты X при условии, что компонента У приняла определенное значение , называется совокупность возможных значений компоненты X и соответствующих этим значениям условных вероятностей , определяемых равенством

(3.6)

Если (X, У) — ДСВ и G — произвольная область на плоскости, то

(3.7)

Двумерный случайный вектор (X, Y) называется непрерывным случайным вектором (НСВ), если функция распределения непрерывна на всей плоскости и существует такая неотрицательная интегрируемая по Риману в бесконечных пределах по каждой из координат функция , называемая плотностью распределения вероятностей случайного вектора (X, У), что

(3.8)

Плотность распределения вероятностей обладает следующими свойствами:

· ;

· - условие нормировки;

· Если - точка непрерывности плотности , то

; (3.9)

· Плотности распределения вероятностей отдельных компонент случайного вектора выражаются в виде интегралов от совместной плотности:

(3.10)

Если (X,Y) — НСВ, то вероятность попадания случайной точки в произвольную квадрируемую область G на плоскости определяется по формуле

(3.11)

Пусть (X, У) — двумерный НСВ. Условной плотностью распределения вероятностей случайной компоненты X при условии, что компонента У приняла определенное значение у такое, что , называется неотрицательная функция f_x(x/y) действительной переменной х, определяемая при всех следующей формулой:

(3.12)

Аналогично, при всех и всех таких, что f_x(x) > 0,

Случайные величины называются независимыми (в совокупности), если для любого набора событий , , где - подмножества числовой прямой, выполняется равенство

Случайные величины независимы тогда и только тогда, когда в любой точке имеет место равенство

(3.13)

Из этого соотношения следует также, что для независимости компонент непрерывного случайного вектора необходимо и достаточно, чтобы в любой точке

(3.14)

Если же - ДСВ, то соответствующее условие независимости его компонент записывается в виде

. (3.15)

Для двумерного случайного вектора (X, У) вводятся следующие числовые характеристики.

Начальным моментом порядка k + s случайного вектора (X, У) называется действительное число определяемое формулой

(3.16)

Начальный момент существует, если ряд (соответственно интеграл) в правой части равенства абсолютно сходится. В частности, - соответствующие начальные моменты отдельных компонент.

Вектор с неслучайными координатами называется математическим ожиданием случайного вектора (X, У) или центром рассеивания.

Центральным моментом порядка k + s случайного вектора (X, У) называется действительное число определяемое формулой

(3.17

Центральный момент существует, если ряд (соответственно интеграл) в правой части равенства абсолютно сходится. В частности, .

Центральный момент называется корреляционным моментом или ковариацией и обозначается . Таким образом, по определению

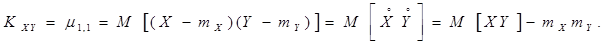(3.18) Нормированная ковариация называется коэффициентом корреляции двух случайных компонент X и Y случайного вектора.

Коэффициент корреляции удовлетворяет условию и определяет степень линейной зависимости между X и Y. Случайные величины, для которых , называются некоррелированными. Из независимости случайных величин X и Y следует их некоррелированность (обратное, в общем случае, неверно).

Приведенные выше формулы для числовых характеристик двумерного случайного вектора (X, У) обобщаются на случай n-мерного случайного вектора . Так вектор с неслучайными координатами , где — математическое ожидание случайной величины , определяемое формулой

(3.19)

называется центром рассеивания случайного вектора .

Ковариационной матрицей n – мерного случайного вектора называется симметрическая действительная матрица, элементы которой представляют собой корреляционные моменты (ковариации) соответствующих пар компонент:

(3.20)

где

Корреляционной матрицей n – мерного случайного вектора называется нормированная ковариационная матрица

(3.21)

где - коэффициент корреляции i – й и j – й компонент.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: