 |
Линеаризация функций случайных величин.
|
|
|
|
Рассмотренный выше метод нахождения числовых характеристик функций случайных величин без определения закона распределения этих функций применим в основном к линейным функциям.
На практике очень часто встречаются случаи, когда исследуемая функция случайных величин хотя и не является строго линейной, но практически мало отличается от линейной и при решении задачи может быть приближенно заменена линейной. Это связано с тем, что во многих практических задачах случайные изменения фигурирующих в них величин выступают как незначительные «погрешности», накладывающиеся на основную закономерность. Вследствие сравнительной малости этих погрешностей обычно фигурирующие в задаче функции, не будучи линейными во всем диапазоне изменения своих аргументов, оказываются почти линейными в узком диапазоне их случайных изменений.
Действительно, из математики известно, что любая непрерывная дифференцируемая функция в достаточно узких пределах измененияаргументов может быть приближенно заменена линейной (линеаризована). Ошибка, возникающая при этом, тем меньше, чем уже границы изменения аргументов и чем ближе функция к линейной. Если область практически возможных значений случайных аргументов настолько мала, что в этой области функция может быть с достаточной для практики точностью линеаризована, то, заменив нелинейную функцию линейной, можно применить к последней тот аппарат числовых характеристик, который разработан для линейных функций. Зная числовые характеристики аргументов, можно будет найти числовые характеристики функции, Конечно: при этом мы получим лишь приближенное решение задачи, но в большинстве случаев точного решения и не требуется.
|
|
|
При решении практических задач, в которых случайные факторы сказываются в виде незначительных возмущений, налагающихся на основные закономерности, линеаризация почти всегда оказывается возможной именно в силу малости случайных возмущений.
Рассмотрим вначале задачу линеаризации функции одного случайного аргумента.
Пусть имеется случайная величина X и известны ее числовые характеристики: mx и Dx.
Допустим, что практически возможные значения случайной величины X ограничены пределами  т. е.
т. е.

Имеется другая случайная величина У, связанная с X функциональной зависимостью:
 (4.8)
(4.8)
причем функция  хотя не является линейной, но мало отличается от линейной на участке
хотя не является линейной, но мало отличается от линейной на участке  .
.
Требуется найти числовые характеристики величины  - математическое ожидание ту и. дисперсию Dy.
- математическое ожидание ту и. дисперсию Dy.
Рассмотрим кривую  на участке
на участке  и заменим её приближенно касательной, проведенной в точке с абсциссой mx. Уравнение касательной имеет вид:
и заменим её приближенно касательной, проведенной в точке с абсциссой mx. Уравнение касательной имеет вид:
 (4.9)
(4.9)
Учитывая малое отличие прямой (4.9) от функции (4.8) на интервале  , заключаем, что случайные величины X и Y приближенно связаны линейной зависимостью:
, заключаем, что случайные величины X и Y приближенно связаны линейной зависимостью:

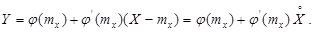 (4.10)
(4.10)
К линейной функции (3.10) можно применить известные приемы определения числовых характеристик линейных функций. Так как математическое ожидание аргумента  в (4.10) равно нулю, то математическое ожидание функции (4.10):
в (4.10) равно нулю, то математическое ожидание функции (4.10):

 (4.11)
(4.11)
Дисперсия величины  определится по формуле
определится по формуле
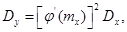 (4.12)
(4.12)
а СКО
 (4.13)
(4.13)
Очевидно, что формулы (4.11), (4.12), (4.13) являются приближенными.
Таким образом, чтобы найти математическое ожидание почти линейной функции, нужно в выражение функции вместо аргумента подставить его математическое ожидание. Чтобы найти дисперсию почти линейной функции, нужно дисперсию аргумента умножить на квадрат производной функции в точке, соответствующей математическому ожиданию аргумента.
Рассмотрим линеаризацию функции нескольких случайных аргументов.
|
|
|
Имеется система  случайных величин (n – мерный случайный вектор):
случайных величин (n – мерный случайный вектор):
 ,
,
заданы числовые характеристики системы: математические ожидания

и ковариационная матрица

Случайная величина  есть функция аргументов
есть функция аргументов  :
:
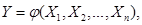 (4.14)
(4.14)
причем функция  не линейна, но мало отличается от линейной в области практически возможных значений всех аргументов («почти линейная» функция). Требуется приближенно найти числовые характеристики величины
не линейна, но мало отличается от линейной в области практически возможных значений всех аргументов («почти линейная» функция). Требуется приближенно найти числовые характеристики величины  - математическое ожидание
- математическое ожидание 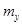 и дисперсию
и дисперсию  .
.
Для решения задачи подвергнем линеаризации функцию
 (4.15)
(4.15)
Разложим функцию (4.15) в ряд Тейлора в окрестности точки  сохраняя члены только до первого порядка малости включительно
сохраняя члены только до первого порядка малости включительно

Введём обозначение:

Тогда зависимость (4.14) можно приближенно заменить линейной зависимостью
 (4.16)
(4.16)
Имея в виду, что центрированные аргументы  имеют математические ожидания, равные нулю, и ту же ковариационную матрицу
имеют математические ожидания, равные нулю, и ту же ковариационную матрицу  , найдем числовые характеристики линейной функции (4.16):
, найдем числовые характеристики линейной функции (4.16):
 (4.17)
(4.17)
 (4.18)
(4.18)
 (4.19)
(4.19)
где  - коэффициент корреляции величин
- коэффициент корреляции величин  .
.
Если величины  не коррелированы, т.е.
не коррелированы, т.е.  при
при  , то
, то
 (4.20)
(4.20)
Формулы (4.18)-(4.20) находят широкое применение в практических задачах.
В некоторых задачах практики возникает сомнение в применимости метода линеаризации в связи с тем, что диапазон изменений случайных аргументов не настолько мал, чтобы в его пределах функция могла быть с достаточной точностью линеаризована.
В этих случаях для проверки применимости метода линеаризации и для уточнения полученных результатов может быть применен метод, основанный на сохранении в разложении функции не только линейных членов, но и некоторых последующих членов более высоких порядков и оценке погрешностей, связанных с этими членами-
Пример
Расстояние  от некоторой точки О до объекта R (рис. 1 ) определяется следующим образом:
от некоторой точки О до объекта R (рис. 1 ) определяется следующим образом:
 |
Рис. 1
измеряется угол  , под которым виден объект из точки О; далее, зная линейный размер объекта X и считая угол
, под которым виден объект из точки О; далее, зная линейный размер объекта X и считая угол  малым, определяют расстояние по приближенной формуле:
малым, определяют расстояние по приближенной формуле:
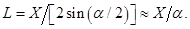
 .
.
Линейный размер объекта X, видимый из точки О, в зависимости от его случайного поворота может изменяться в пределах от 8 до 12 м; угол  определяется с точностью до 0,0001 радиана. Расстояние
определяется с точностью до 0,0001 радиана. Расстояние  велико по сравнению с размером объекта X. Угол
велико по сравнению с размером объекта X. Угол  измеряется без систематической ошибки. Результат измерения
измеряется без систематической ошибки. Результат измерения  радиана. Найти приближенно среднее квадратическое отклонение
радиана. Найти приближенно среднее квадратическое отклонение  ошибки в определении расстояния
ошибки в определении расстояния  .
.
|
|
|
Решение. Применяя метод линеаризации, имеем

Линейный размер 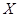 будем считать равномерно распределенным в интервале (8; 12) -
будем считать равномерно распределенным в интервале (8; 12) -  :
:
 ;
; 
Результат измерения угла  будем считать нормально распределенной случайной величиной с математическим ожиданием
будем считать нормально распределенной случайной величиной с математическим ожиданием  и средним квадратическим отклонением
и средним квадратическим отклонением  (в соответствии с правилом «трёх сигм»):
(в соответствии с правилом «трёх сигм»):  . Тогда
. Тогда

|
|
|


