 |
Федеральное государственное бюджетное образовательное учреждение
|
|
|
|
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Башкирский Государственный Медицинский Университет»
МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Кафедра медицинской физики с курсом информатики
МЕТОДИЧЕСКИЕ РАЗРАБОТКИ ПО ЛЕКЦИЯМ
Дисциплина «Физика, математика»
Специальность 31. 05. 01 Лечебное дело
Курс ________ I_______________
Семестр ______1_______________
Количество часов ___21________
Уфа 2018
Методические разработки лекций на основании рабочей программы по дисциплине «Физика, математика», утвержденной «29» июня 2018 г.
Рецензенты:
Заведующий кафедрой биохимии БГМУ, профессор, д. м. н. Ш. Н. Галимов
Доцент кафедры теоретической физики БГУ, к. ф. -м. н. А. Т. Харисов
Утверждено на заседании № 1 кафедры медицинской физики с курсом информатики от 29 августа 2018 г.
Составитель: Закирьянова Г. Т.
Тема1: Основы математического анализа
1. Курс: первый семестр: первый
2. Продолжительность лекции: 1 ч.
3. Контингент слушателей: студенты педиатрического факультета
4. Учебная цель: изучение основ математического анализа, изучить понятия производной и дифференциала функции, ознакомиться с основными правилами дифференцирования и производными элементарных функций.
5. Иллюстративный материал и оснащение: мультимедийный проектор, ноутбук.
6. Подробный план:
1) Производные и дифференциалы. Применение методов дифференциального исчисления для анализа функций. Производные сложных функций.
2) Правила интегрирования. Вычисление неопределенных и определённых интегралов.
|
|
|
3) Методы решения дифференциальных уравнений первого порядка с разделяющимися переменными.
7. Методы контроля знаний и навыков: традиционные методы контроля.
8. Литература: см. в приложении.
Производная функции.
Пусть на некотором промежутке X определена функция y=f(x). Возьмем любую точку x0 из промежутка X и зададим аргументу x в точке x0 произвольное приращение ∆ x такое, что точка x0+∆ x также принадлежит X. Функция получит приращение ∆ y=f(x0+∆ x) – f(x0).
Определение. Производной функции y=f(x) в точке x0 называется предел при ∆ x→ 0 отношения приращения функции в этой точке к приращению аргумента (при условии, что этот предел существует).
Итак, по определению,
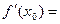
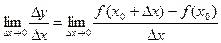
Функция y=f(x), имеющая производную в каждой точке промежутка X, называется дифференцируемой в этом промежутке; операция нахождения производной функции называется дифференцированием.
Геометрический смысл производной.
Рассмотрим график непрерывной кривой y=f(x), имеющий в точке (x, y) невертикальную касательную. Угловой коэффициент касательной
k=tgα =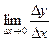 
, где α – угол касательной с осью Оx.
Это равенство перепишем в виде f`(x)=tgα =k, т. е. производная f`(x) в точке x равна угловому коэффициенту касательной к графику функции y=f(x) в точке (x, f(x)). В этом заключается геометрический смысл производной.
Механический смысл производной.
Скорость прямолинейного движения материальной точки в момент времени t есть производная от пути S по времени t.
Производная суммы, разности, произведения и частного функций.
Пусть функции u=u(x) и v=v(x) – две дифференцируемые в некотором интервале (a, b) функции.
Теорема. Производная суммы (разности) двух функций равна сумме (разности) производных этих функций: (u±v)`=u`±v`.
Обозначим y=u±v. По определению производной и основным теоремам о пределах получаем:
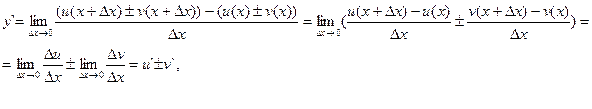
т. е. (u±v)`=u`±v`.
|
|
|
Теорема справедлива для любого конечного числа слагаемых.
Теорема. Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго: (u∙ v)`=u`v+uv`.
Пусть y=uv. Тогда
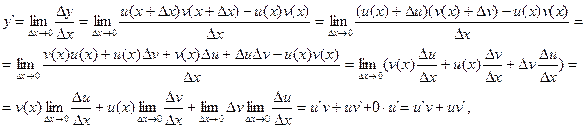
т. е. (u∙ v)`=u`v+uv`.
Теорема. Производная частного двух функций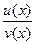 
, если v(x)≠ 0 равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя: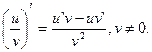 
Пусть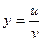 
. Тогда
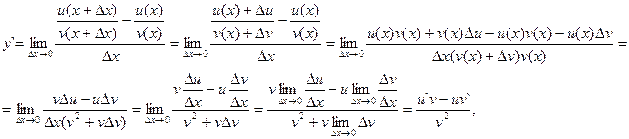
т. е.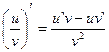 
|
|
|
