 |
Классическое определение вероятности
|
|
|
|
Классическое определение вероятности
Под вероятностью Р(А) наступления события будем понимать отношение числа исходов (m), благоприятствующих наступлению данного события, к числу всех исходов (несовместных, единственно возможных и равновозможных) испытания (n):
P(A) = m/n (1)
Для случайного события m < n; для достоверного события m = n; для невозможного события m = 0.
Границы значений вероятности события: 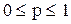
Пример 3. 1. Какова вероятность появления нечетной грани при бросании кости.
Решение. Появление нечетной грани при бросании кости (событие А) происходит при выпадении 1, или 3, или 5, т. е. здесь m = 3, поэтому
Р(А) = 3/6 = 1/2
Теорема сложения вероятностей
Суммой двух событий А и В называется событие С, состоящее в наступлении события А, или события В, или событий A и B одновременно.
Теорема. Вероятность наступления одного из двух несовместных событий А и В равна сумме вероятностей событий А и В:
Р(А + В) = Р(А) + Р(В). (2)
Следствие. Сумма вероятностей двух противоположных событий равна 1.
Р(А) + Р(А) = 1
Решение: Событие В явление противоположным А, следовательно
Р(В) = 1 – Р(А) = 1 – 0, 516 = 0, 484.
Теорема. Сумма вероятностей несовместных событий А1, А2, ..., Аn, образующих полную группу событий, равна 1:
Р(А1) + Р(А2) +... + Р(Аn) = 1. (3)
Теорема умножения вероятностей
Теорема. Вероятность совместного наступления двух зависимых событий равна произведению вероятности наступления первого события на условную вероятность наступления второго события, вычисленную в предположении, что первое событие имеет место:
|
|
|
Р(АВ) = Р(А) ´ Р(В/А). (4)
Пример 3. 3. Найти вероятность двукратного извлечения белого шара из урны, в которой из 12 шаров имеется 7 белых, если вынутый шар в урну не возвращается.
Решение: Событие А – появление белого шара первый раз, событие В –появление белого шара второй раз.
Событие А и В зависимы и Р(А) = 7/12, Р(В/А) = 6/11.
Поэтому Р(А В) = Р(А)× Р(В/А) = (7/12)× (6/11) = 7/22.
Теорема. Вероятность одновременного наступления в некотором опыте двух независимых событий равна произведению вероятностей этих событий:
Р(АВ) = Р(А)× Р(В). (5)
Рассмотрим предыдущий пример для случая, когда вынутый шар возвращается обратно в урну. Тогда событие А и В независимы и Р(А) = Р(В) = 7/12.
Р(А В) = Р(А)× Р(В) = (7/12)× (7/12) = 49/144.
Теорема полной вероятности
Теорема. Вероятность события А, которое может осуществиться лишь при условии осуществления одного из несовместных событий А1, А2, ..., Аn, образующих полную группу, равна сумме произведения вероятностей каждого из этих событий на соответствующую условную вероятность события А:
Р(А) = Р(А1)× Р(А/А1) + Р(А2)× Р(А/А2) +... + Р(Аn)× Р(А/Аn), (6)
или 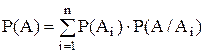
Пример 3. 4. Пластмассовые болванки изготовляются на трех прессах. 1-й пресс вырабатывает 50% всех болванок, 2-й – 30% и 3-й – 20%. При этом: из болванок с 1-го пресса в среднем 0, 025 нестандартных, со 2-го – 0, 020, с 3-го – 0, 015. Найти вероятность того, что наудачу взятая со склада болванка соответствует стандарту.
Решение: Р(А1) = 0, 5; Р(А2) = 0, 3 и Р(А3) = 0, 2; Р(А/А1) = 0, 025; Р(А/А2) = 0, 020; Р(А/А3) = 0, 015 (событие А1 – появление болванки с 1-го пресса, А2 – со 2-го пресса, А3 – с 3-го пресса, (А/А1, 2, 3) – появление нестандартной болванки с 1-го, 2-го или 3-го пресса соответственно).
|
|
|
Если событие Е обозначает соответствие болванки стандарту, то для отдельных прессов имеем следующее условные вероятности выпуска стандартных болванок:
Р(E/А1) = 0, 975, Р(Е/А2) = 0, 980 и Р(Е/А3) = 0, 985.
Отсюда Р(Е) = 0, 5× 0, 975 + 0, 3× 0, 98 + 0, 2× 0, 985 = 0, 9785, т. е. вероятность того, что взятая наудачу со склада болванка стандартна, равна 0, 9785.
Формула Байеса
А1, А2,..., Аn – несовместные события, образующую полную группу событий; событие Е может наступить лишь совместно с одним из событий Аj. Если событие Е уже произошло, то вероятности событий Aj могут быть определены по формуле Байеса:
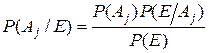 . (7)
. (7)
где Р(Е) = 
Пример 3. 5. По условию предыдущего примера вычислить вероятность того, что соответствующая стандарту болванки изготовлена: а) на 1-ом, б) на 2-ом, в) на 3-м прессе.
Решение: а) для гипотезы А1, пользуясь формулой Байеса, получаем:
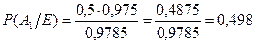 ;
;
б) для гипотезы А2 имеем:
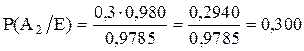 ;
;
в) для гипотезы А3 имеем:
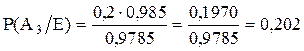 .
.
Правильность вычислений подтверждается тем, что:
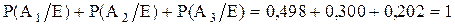 .
.
1. Тема3: Основы математической статистики
2. Курс: первый семестр: первый
3. Продолжительность лекции: 1 час
4. Контингент слушателей: студенты
5. Учебная цель: изучение основ математической статистики
6. Иллюстративный материал и оснащение: интерактивная доска
7. Подробный план:
1) Непрерывные и дискретные случайные величины.
2) Распределение дискретных и непрерывных случайных величин, их характеристики: математическое ожидание, дисперсия, среднее квадратичное отклонение.
3) Нормальный и экспоненциальный законы распределения непрерывных случайных величин.
4). Функция распределения. Плотность вероятности. Стандартные интервалы.
8. Методы контроля знаний и навыков: традиционные методы контроля.
9. Литература: см. в приложении.
|
|
|


