 |
Дифференциальные уравнения первого порядка с разделяющимися переменными.
|
|
|
|
Пример.
Общим решением дифференциального уравнения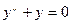 
является 
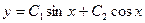. Найти частное решение, если при 
, 
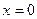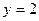и 
.
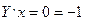Решение.
Из общего решения получим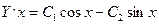 
. Из условия, что при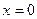 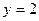, а .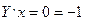
Найдем значение постоянных 
и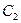 
и подставим в общее решение
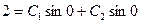. Откуда 
;
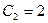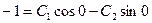. Откуда 
.
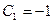Искомое частное решение в этом случае будет иметь вид
.
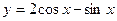Дифференциальные уравнения первого порядка с разделяющимися переменными.
Уравнение вида 
называется уравнением с разделяющимися переменными.
Оно может быть приведено к уравнению с разделенными переменными путем деления обеих его частей на выражение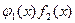 
;
, откуда
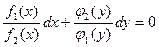(1).
Равенство (1) можно считать суммой двух дифференциалов. Интегрируя его, получим
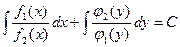, где С- постоянная интегрирования (2).
Выражение (2). Является общим решением уравнения (1).
Пример.
Найти общее и частное решение уравнения-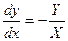 
.
Начальные данные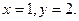 
Решение.
В уравнении 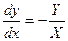путем умножения обеих частей на 
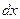разделим дифференциалы: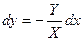 
Разделив обе части последнего уравнения на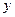 
, получим уравнение с разделенными переменными: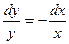 
Проинтегрируем последнее уравнение:
; 
; 
.
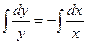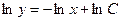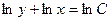Потенцируя последнее равенство, получим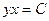 
или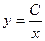 
- общее решение уравнения .
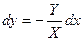Подставив в общее решение начальные условия, т. е. 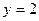и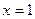 
, потом 
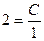, откуда 
.
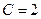Подставив в общее решение значение 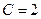, получим частное решение уравнения: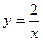 
1. Тема 2: Понятие о доказательной медицине. Случайное событие. Определение вероятности.
2. Курс: первый семестр: первый
3. Продолжительность лекции: 2 ч.
4. Контингент слушателей: студенты педиатрического факультета
5. Учебная цель: изучение основ теории вероятностей
6. Иллюстративный материал и оснащение: мультимедийный проектор, ноутбук.
|
|
|
7. Подробный план:
1) Понятие о доказательной медицине.
2) Случайное событие. Определение вероятности.
3) Понятие о совместных и несовместных событиях, зависимых и независимых событиях.
4)Теоремы сложения и умножения вероятностей)
8. Методы контроля знаний и навыков: традиционные методы контроля.
9. Литература: см. в приложении.
Случайные события
Теория вероятностей изучает закономерности массовых явлений, носящих случайный характер. Многие явления в природе, технике, экономике и в других областях носят случайный характер, т. е. невозможно точно предсказать, как явление будет происходить. Оказывается, однако, что течение и таких явлений может быть описано количественно, если только они наблюдались достаточное число раз при неизменных условиях. Теория вероятностей дает математическую модель для описания случайных явлений такого рода в объективной действительности. Так как многие реальные процессы подвержены случайным воздействиям, то основы этой теории важно знать специалистам, занимающимся естественными, техническими, общественными науками.
Методы теории вероятностей и математической статистики нашли широкое применение при обработке данных экспериментов и при решении ряда прикладных задач во всех областях науки и техники, в разработке математических методов медицинской диагностики, в организации здравоохранения и т. д.
Изучение закономерностей однородных массовых случайных явлений составляет предмет теории вероятностей и основанной на ней математической статистики. При этом изучаемые явления рассматриваются в абстрактной форме, независимо от их конкретной природы.
Изучение каждого явления в порядке наблюдения или выполнения опыта связано с выполнением некоторого комплекса условий, или испытанием. Результат испытания будем называть событием. Так, событиями являются: зеленый, желтый, и красный цвета на светофоре к моменту прибытия пешехода к перекрестку; частые и редкие звуковые сигналы в слуховой части телефонной трубки в результате набора на диске некоторого номера и др.
|
|
|
Определение. События называются несовместными, если в условиях испытания каждый раз возможно появления только одного из них.
Пример. Событие А – поражение мишени в результате произведенного выстрела, событие В – не поражение мишени. Эти события являются несовместными.
Определение. События называются совместными, если в данных условиях появление одного из этих событий не исключает появления другого при том же испытании.
Пример. При бросании игрального кубика совместными событиями будут события: появление нечетного числа очков и появление одного очка.
Определение. Событие называется достоверным, если оно является единственно возможным исходом испытания.
Пример. Достоверным событием является извлечение черного шара из урны, в которой все шары черные.
Определение. Событие называется невозможным, если оно не может произойти.
Пример. Невозможным событием является извлечение белого шара из урны, в которой все шары черные.
Определение. Событие называют случайным, если результат испытания приводит либо к появлению, либо к непоявлению этого события.
Пример. Случайным событием являются извлечение белого шара из урны, в которой находятся шары, различные по своему цвету, включая и белый.
Определение. Если в результате опыта непременно должно появиться одно из рассматриваемых событий, то их называют полной группой событий.
Например, давление крови может быть нормальное, повышенное или пониженное.
Определение. Два несовместных события, составляющих полную группу, называются противоположными.
Например, при бросании монеты появление герба и цифры.
Определение. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.
Например, температура тела у одного больного не зависит от того, какая она у первого.
Определение. Событие А называется зависимым от события В, если вероятность события А зависит от того, произошло событие В или нет.
|
|
|
|
|
|
