 |
Производная сложной и обратной функций.
|
|
|
|
Производная сложной и обратной функций.
Пусть y=f(u) и u=φ (x), тогда y=f(φ (x))-сложная функция.
Теорема. Если функция u=φ (x) имеет производную ux` в точке x, а функция y=f(u) имеет производную yu` в соответствующей точке u=φ (x), то сложная функция y=f(φ (x)) имеет производную yx` в точке x, которая находится по формуле yx`=yu`ux`.
Пусть y=f(x) и x=φ (y) – взаимно обратные функции.
Теорема. Если функция y=f(x) строго монотонна на интервале (a, b) и имеет неравную нулю производную f`(x) в произвольной точке этого интервала, то обратная ей функция x=φ (y) также имеет производную φ `(y) в соответствующей точке, определяемую равенством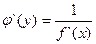 
или 
.
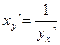Неопределенный интеграл
Определение 1. Функция F(x) называется первообразной для функции f(x), если для всех x их области определения функции F`(x)=f(x) или dF(x)=f(x)dx
Пример1: Функция 3х2 есть производная от х3. Следовательно, для f(x)=3х2 функция F(x)=x3 является первообразной:
3х2dx=dx3=d(x3+C).
Определение 2. Совокупность первообразных F(x)+C для данной функции f(x) или для данного дифференциала f(x)dx называется неопределенным интегралом.
Неопределенный интеграл выражения f(x)dx обозначается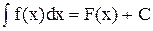 
(1)
Выражение f(x)dx называется подынтегральным выражением,
функция f(x)- подынтегральной функцией,
переменная x- переменной интегрирования.
F(x) в правой части формулы (1) называется функциональной частью неопределнного интеграла,
С- постоянной интегрирования.
Интегрирование функции f(x) -это отыскание её первообразной F(x).
Пример 2: Найти неопределнный интеграл выражения cos x dx.
Решение: Функция cos x есть производная от функции sin x. Поэтому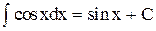 
.
|
|
|
Простейшие способы интегрирования
1. Непосредственное интегрирование
Нахождение интегралов функций, основанное на прямом применении свойств неопределенных интегралов и формул интегрирования, называется способом непосредственного интегрирования.
Пример: Найти 
(2х3-3х2+2х-7)dx
Решение: В данном примере под знаком интеграла стоит алгебраическая сумма функций. По свойству 5 неопределнных интегралов имеем (2х3-2х2+2х-7)dx= 2х3dx- 3х2dx+ 2хdx- 7dx.
Последовательно применяя свойство 4 интегралов и формулы 1, 2 таблицы основных интегралов, получаем следующий результат:
(2х3-3х2+2х-7)dx=2 х3dx-3 x2dx+2 xdx-7 dx=2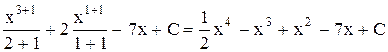 
2. Интегрирование подстановкой
Способ подстановки заключается в переходе от данной переменной иентегрирования к другой переменной, для того чтобы упростить подынтегральное выражение и привести к одному из табличных.
Пример: Найти интеграл 
Решение: Если бы надо было взять 
dx, то это можно записать как х1/2dx и взять интеграл от степенной функции. Поэтому в нашем случае имеет смысл ввести подстановку х+1=t.
Дифференцирование даёт: d(x+1)dt, dx=dt. = 
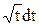= t1/2dt=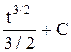 
Подставим вместо t его значение х+1. Получим =2/3(х+1)3/2+С
Интегрирование по частям
Интегрирование по частям называется сведение данного интеграла u dv к интегралу v du при помощи формулы u dv=uv- v du.
Пример: Найти интеграл ln x dx
Решение: Обозначим ln x через u, тогда dx=dv. Находим
du=d(ln x)=(ln x)`x dx=1/x dx; dv= dx, v=x.
Используя формулу для интегрирования по частям, получим
ln x dx=x lnx- x. 1/X dx=x ln x-x+C=x(ln x-1)+C.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определение:
Если существует конечный предел интегральной суммы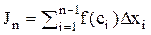 
при условии, что max 
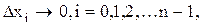то этот предел называют определенным интегралом от функции f(x) на отрезке [a, b].
Определнный интеграл обозначается:
|
|
|
J=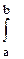 
f(x) dx
Согласно определению, = 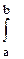f(x) fx=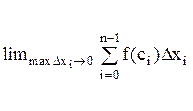 
В выражении определенного интеграла функция f(x) называется подынтегральной, х-переменной интегрирования, числа a и b-соответственно нижним и верхним пределами интегрирования.
|
|
|
