Поиск числа компонент связности графа

Для этого следует в матрице достижимости выделить блоки наибольшей связности вершин графа. Число таких блоков определит число компонент k(G).

 

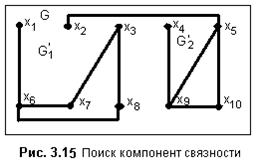
Пример: на рис. 3.15 дан граф G=<x, r>. Определить k(G).

В таблице r приведена матрица смежностей графа G

1, если x_i смежна x_j,

r(i, j)=

0, в противном случае.

Ниже приведены матрица смежности и матрица достижимости ||q||=IÈ||r||, элементы которой определяют по формуле q(i, j) = 1(i, i) Ú r(i, j) при i¹j.

 

 

r	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10
x1
x2
x3
x4
x5
x6
x7
x8
x9
x10

 

q	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10
x1
x2
x3
x4
x5
x6
x7
x8
x9
x10

В таблице r² элементы определяют по формуле:

r² (i, j) =_k=1 Ú ⁿ (r(i, k) × r(k, j)).

r2	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10
x1
x2
x3
x4
x5
x6
x7
x8
x9
x10

В таблице q² элементы определяют по формуле:

q²(i, j) =q(i, j) Ú r ² (i, j) при i¹j.

q2	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10
x1
x2
x3
x4
x5
x6
x7
x8
x9
x10

 

В таблице r³ элементы определяют по формуле:

r³(i, j) =_k=1 Ú ⁿ (r(i, k) × r²(k, j)).

r3	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10
x1
x2
x3
x4
x5
x6
x7
x8
x9
x10

В таблице q³ элементы определяют по формуле:

q³(i, j) =q²(i, j) Ú r ³ (i, j) при i¹j.

q3	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10
x1
x2
x3
x4
x5
x6
x7
x8
x9
x10

Дальнейший поиск q⁴, q⁵,...не приводит к изменению матриц достижимости.

Выполняя перестановку строк и столбцов матрицы q³, получим два блока связности.

q3	x1	x3	x6	x7	x8	x2	x4	x5	x9	x10
x1
x3
x6
x7
x8
x2
x4
x5
x9
x10

Следовательно, граф G=<X, r> содержит два связных подграфа G’₁ и G'₂, т. е. k(G)=2.

Поиск устойчивости графа

Для поиска внутренней и внешней устройчивости графа удобно использовать списки смежных вершин для каждой вершины x_i, т. е. найти Xa={h(x_i)}ÍX, и дополнить их списками несмежных вершин X_b={ùh(x_i)}ÍX.

Поиск внутренней устройчивости. Если существуют элементы, принедлежащие X_b={ùh(x_i)}ÍX, то сформировать из вершин x_iÎX и каждой вершины множества X_b двухэлементные множества:

S₁={{x_i, ùh(x_i)}}Í(XÄX).

Для каждой пары {x_i, ùh(x_i)} найти множество несмежных вершин

X_b2={{ùh(x_i, ùq(x_i))}}ÍX.

Если существуют элементы X_b2, то сформировать из вершин, принадлежащих {x_i, ùh(x_i)}, и каждой вершины множества X_b2 трехэлементные множества:

S₂={{x_i, ùh(x_i), ùh(x_i, ùh(x_i}))}Í(XÄXÄX).

Для каждой тройки попарно несмежных вершин {x_i, ùh(x_i) ùh(x_i, ùh(x_i))} найти множество несмежных вершин

X_b3={{ùh(x_i, ùh(x_i), ùh(x_i, ùh(x_i)))}}ÍX.

Если существуют элементы X_b3, то сформировать из вершин, принадлежащих {x_i, ùh(x_i), ùh(x_i, ùh(x_i))}, и каждой вершины множества X_b3 четырехэлементные множества:

S₃={{x_i, ùh(x_i), ùh(x_i, ùh(x_i)), ùh(x_i, ùh(x_i), ùh(x_i, ùh(x_i)))}}Í(XÄXÄXÄX).

Для каждой четверки попарно несмежных вершин {x_i, ùh(x_i) ùh(x_i, ùh(x_i)), ùh(x_i, ùh(x_i), ùh(x_i, ùh(x_i)))} найти множество несмежных вершин.

X_b4={{ùh(x_i, ùh(x_i) ùh(x_i, ùh(x_i)), ùh(x_i, ùh(x_i), ùh(x_i, ùh(x_i))))}}ÍX.

Процедуру продолжать до тех пор пока для всех подмножеств S_i={{x_i, ùh(x_i) ùh(x_i, ùh(x_i)), ùh(x_i, ùh(x_i), ùh(x_i, ùh(x_i)))....}} не будет выполнено_..условие:

ùh({x_i, ùh(x_i) ùh(x_i, ùh(x_i)), ùh(x_i, ùh(x_i), ùh(x_i, ùh(x_i)))...})={Æ}

Таких подмножеств может быть несколько. Наибольшее число попарно несмежных вершин есть число внутренней устройчивости графа, т. е. j(G)=max{|S_i|}.

 

Пример: на рис. 3.16 дан граф. Определить его внутреннюю устойчивость.

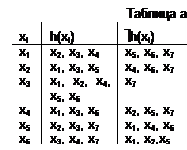
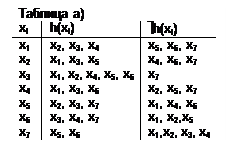
Для графа сформируем списки смежных h(x_i) и несмежных ùh(x_i) вершин (см. таблицу а). Так как в таблице есть несмежные вершины, то сформируем подмножества попарно несмежных вершин {x_i, ùh(x_i)} и найдем списки смежных h(x_i, ùh(x_i)) и несмежныx вершин - ùh(x_i, ùh(x_i)) (см. таблицу b). Поскольку для некоторых пар вершин {x_i, ùh(x_i)} есть несмежные вершины ùh(x_i,ùh(x_i)), то сформируем трехэлементные множества несмежных вершин {(x_i, ùh(x_i), (ùh(x_i, ùh(x_i)))} и найдем списки смежных h((x_i, ùh(x_i), (ùh(x_i, ùh(x_i)))) и несмежныx вершин ùh((x_i, ùh(x_i), (ùh(x_i, ùh(x_i)))) (см. табл. c).

В таблице для всех (x_i, ùh(x_i), (ùh(x_i, ùh(x_i))) значение ùh(x_i, ùh(x_i), ùh(x_i, ùh(x_i)))=Æ.

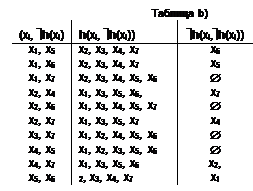
Следовательно, подмножества, содержащие наибольшее число попарно несмежных вершин, есть S={{x₁, x₅, x₆}; {x₂, x₄, x₇}}, т. е. число внутренней устойчивости графа j(G)=max_i{|S_i|}=3.

Поиск внешней устойчивости. Для этого также удобно использовать списки смежных X_a={h(x_i)}ÍX и несмежных вершин X_b={ùh(x_i)}ÍX.

Если существуют элементы xÎX_b, то из пары элементов x_i, x_jÎX при i¹j сформировать двухэлементные множества:

{x_i, x_j}Í(XÄX).

Для каждой пары {x_i, x_j) найти несмежные вершины:

X_b2={ùh(x_i, x_j))}ÍX.

Если существуют xÎX_b2, то из трех элементов x_i, x_j, x_kÎX при i¹j¹k сформировать трехэлементные множества:

{x_i, x_j, x_k}Í(XÄXÄX).

Для каждой тройки {x_i, x_j, x_k} найти несмежных вершин:

X_b3={ùh(x_i, x_j, x_k }ÍX.

Процедуру продолжать до тех пор пока хотя бы для одного подмножества T_i={x_i, x_j, x_k...}Í(XÄXÄX...) не будет выполнено_. усло- вие:

ùh(x_i, x_j, x_k...)=Æ.

Таких подмножеств T_i может быть несколько. Наименьшее число вершин множества Т_i есть число внешней устройчивости, т. е

f(G)=min{|T_i|}.

 

Пример: На рис. 3.16 дан граф. Определить его внешнюю устойчивость.

Сформируем, как и для внутренней устойчивости, списки смежных h(x_i) и несмежных ùh(x_i) вершин (см. таблицу а).

Так как в таблице для всех значений x_i есть несмежные вершины, то сформируем двухэлементные подмножества множества X и найдем списки смежных h(x_i, x_j) и несмежных вершин ùh(x_i,, x_j) (см. таблицу b).

Анализ таблицы пока- зывает, что существуют двух- элементные подмножества, смежные со всеми оставши- мися вершинами графа G. Следовательно, множества, содержащие наименьшее число вершин, смежных со всеми оставшимися вершинами графа, есть T={{x₁, x₇}; {x₂, x₆}; {x₃, x₅}; {x₃, x₆}; {x₃, x₇}; {x₄, x₅}}, т. е. число внешней устойчивости графа f(G)=min_i{|T_i|}=2.

 

таблица b) продолжение таблицы b)
{xi, xj}	h{xi, xj}	ùh{xi, xj}		{xi, xj}	h{xi, xj}	ùh{xi, xj}
x1, x2	x3, x4, x5	x6, x7		x3, x4	x1, x2, x5, x6	x7
x1, x3	x2, x4, x5, x6	x7		x3, x5	x1, x2, x4, x6, x7	Æ
x1, x4	x2, x3, x6	x5, x7		x3, x6	x1, x2, x4, x5, x7	Æ
x1, x5	x2, x3, x4, x7	x6		x3, x7	x1, x2, x4, x5, x6	Æ
x1, x6	x2, x3, x4, x7	X5		x4, x5	x1, x2, x3, x6, x7	Æ
x1, x7	x2, x3, x4, x5, x6	Æ		x4, x6	x1, x4, x7	x2, x5
x2, x3	x1, x4, x5, x6	x7		x4, x7	x1, x3, x5, x6	x2
x2, x4	x1, x3, x5, x6	x7		x5, x6	x2, x3, x4, x7	x1
x2, x5	x1, x3, x7	x4, x6		x5, x7	x2, x3, x6	x1, x4
x2, x6	x1, x3, x4, x5, x7	Æ		x6, x7	x3, x4, x5	x1, x2
x2, x7	x1, x3, x5, x6	x4

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: