Главная | Обратная связь | Поможем написать вашу работу!
 МегаЛекции

Поиск кратчайших путей в сети.




Подобные задачи возникают при выборе маршрутов в вычислительных сетях и транспортных системах. В вычислительных сетях решение подобных задач определяет состав и структуру сетевых протоколов для обслуживания движения пакетов информации. По данным о загрузке каналов, направлении и протяженности вычисляется наиболее оптимальный маршрут прохождения пакета информации. При нахождении такого пути к пакету добавляется заголовок, в котором указывают перечень узлов для перехода от вершины хi к вершине хj или очередную вершину перехода. В транспортных системах решение подобных задач определяет наиболее экономный по стоимости или по времени маршрут движения транспортной единицы.

Каждая вершина в таком графе используется только один раз (простой маршрут), а длина кратчайшего пути определится суммой весов ребер на переходе ni,j=(хi;...хk;...хj):

Li,j=m,nå lm,n, где i£m, n£j, m¹n.

Для поиска кратчайших путей существует несколько алгоритмов. Алгоритмы Форда-Беллмана и Дейкстра позволяют найти кратчайшие пути от заданной вершины графа до любой другой. В результате этих вычислений формируется древовидный остов с корнем в заданной вершине.

Алгоритмы Флойда и Данцига позволяют искать кратчайшие пути между любой парой вершин сети.

В основе всех алгоритмов лежит операция сравнения двух простых маршрутов.

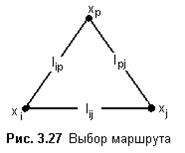На рис. 3.27 показаны два простых маршрута, соединяющих вершины хi и хj. Выбор крат- чайшего пути между вершинами

есть результат сравнения длин двух маршрутов, т.е.

Li,j=min{li,j; (li,p+ lp,j)}.

Если существует несколько вершин, смежных с вершинами хi и хj следует выполнять процедуру последовательно, сравнивая длины маршрутов для каждой вершины.

Для того, чтобы определять по алгоритму Флойда. кратчайшие путь и переходы между вершинами xi и xj, необходимо использовать две матрицы: матрицу кратчайших путей ║l(n;n)║ и матрицу кратчайших переходов ║n(n;n)║, которые позволяют сравнивать различные маршруты через базовую вершину xp.

Вершина хp в матрице кратчайших путей называется базовой, а строка и столбец матрицы ║lp║ - базовыми (выделены в матрице штриховкой), если она позволяет сравнивать кратчайшие пути между любой парой вершин xi и xj, смежных с вершиной хp. Базовая вершина

позволяет найти путь из вершины xi в вершину xj через вершину xp по формуле lij=(lip+ lpj), представить этот результат для сравнения с имеющимся значением lij и выбрать наименьшее значение.

 

lp x0 .. xi .. xp .. xj   np x0 .. xi .. xp .. xj
x0   .. l0i .. l0p .. l0j   x0 x0 .. xi .. xp .. xj
... ...   ... .. ... .. ...   ... x0 .. xi .. xp .. xj
xi li0 ..   .. lip .. lij   xi x0 .. xi .. xp .. xj
... ... .. ...   ... .. ...   ... x0 .. xi .. xp .. xj
xp lp0 .. lpi ..   .. lpj   xp x0 .. xi .. xp .. xj
... ... .. ... .. ...   ...   ... x0 .. xi .. xp .. xj
xj ljo .. lji .. ljp ..     xj x0 .. xi .. xp .. xj

Если в качестве базовой, использовать последовательно все вершины, начиная с х0, то за p=(n-1) шагов итерации можно найти кратчайшие пути между любой парой вершин. Для p=0 матрица ║l0║ есть матрица весов графа.

Для p=0 элементы матрицы n0 есть концевые вершины перехода из хi в хj. Поэтому в каждом столбце хj матрицы n0 указана вершина хj. На p-м шаге итерации происходит замена вершины перехода вершиной кратчайшего перехода по формулам:

а) если (li,p+ lp,j)p³li,jp, то ni,j (p+1) = ni,j p=хj;

b) если (li,p+ lp,j)p<li,jp, то ni,j (p+1)=хp.

Следовательно, для анализа n-вершинного графа необходимо последовательно построить (n-1) матриц.

Алгоритм Флойда:

шаг 1: составить матрицу весов ║lp║ и матрицу переходов ║np║ для p=0, где p – шаг итерации;

шаг 2: определить вершину p базовой и выделить базовые строки и столбец;

шаг 3: вычеркнуть строки и столбцы, базовые элементы которых имеют значение ¥, т.к. (li,p+¥) и (¥+ lp,j) всегда больше конечного значения li,j;

шаг 4: сравнить каждый невычеркнутый элемент lijp с суммой (li,p+ lp,j)p для формирования значений li,j и ni,j на очередном шаге итерации:

a) если (li,p+ lp,j)p<li,jp, то li,jp+1=(li,p+ lp,j)p, а ni,j (p+1)=p;

b) если (li,p+ lp,j)p>li,jp, то li,jp+1=li,jp; ni,j (p+1)= ni,j p.

шаг 5: если p<n, то принять p=p+1 и вернуться к шагу 4, иначе конец.

Пример: Найти кратчайшие пути на графе (см. рис. 3.28).

 
 

Ниже таблицами показан процесс вычисления от p=0 до p=7

 

l0 x0 x1 x2 x3 x4 x5 x6 x7   n0 x0 x1 x2 x3 x4 x5 x6 x7
x0     ∞   ∞ ∞ ∞ ∞   x0 x0 x1 x2 x3 x4 x5 x6 x7
x1       ∞   ∞ ∞ ∞   x1 x0 x1 x2 x3 x4 x5 x6 x7
x2 ∞             ∞   x2 x0 x1 x2 x3 x4 x5 x6 x7
x3   ∞     ∞ ∞   ∞   x3 x0 x1 x2 x3 x4 x5 x6 x7
x4 ∞     ∞     ∞     x4 x0 x1 x2 x3 x4 x5 x6 x7
x5 ∞ ∞   ∞           x5 x0 x1 x2 x3 x4 x5 x6 x7
x6 ∞ ∞     ∞         x6 x0 x1 x2 x3 x4 x5 x6 x7
x7 ∞ ∞ ∞ ∞           x7 x0 x1 x2 x3 x4 x5 x6 x7
                                     
l1 x0 x1 x2 x3 x4 x5 x6 x7   n1 x0 x1 x2 x3 x4 x5 x6 x7
x0     ∞   ∞ ∞ ∞ ∞   x0 x0 x1 x2 x3 x4 x5 x6 x7
x1           ∞ ∞ ∞   x1 x0 x1 x2 x0 x4 x5 x6 x7
x2 ∞             ∞   x2 x0 x1 x2 x3 x4 x5 x6 x7
x3         ∞ ∞   ∞   x3 x0 x0 x2 x3 x4 x5 x6 x7
x4 ∞     ∞     ∞     x4 x0 x1 x2 x3 x4 x5 x6 x7
x5 ∞ ∞   ∞           x5 x0 x1 x2 x3 x4 x5 x6 x7
x6 ∞ ∞     ∞         x6 x0 x1 x2 x3 x4 x5 x6 x7
x7 ∞ ∞ ∞ ∞           x7 x0 x1 x2 x3 x4 x5 x6 x7
l2 x0 x1 x2 x3 x4 x5 x6 x7   n2 x0 x1 x2 x3 x4 x5 x6 x7
x0           ∞ ∞ ∞   x0 x0 x1 x1 x3 x1 x5 x6 x7
x1           ∞ ∞ ∞   x1 x0 x1 x2 x0 x4 x5 x6 x7
x2               ∞   x2 x1 x1 x2 x3 x4 x5 x6 x7
x3           ∞   ∞   x3 x0 x0 x2 x3 x1 x5 x6 x7
x4             ∞     x4 x1 x1 x2 x1 x4 x5 x6 x7
x5 ∞ ∞   ∞           x5 x0 x1 x2 x3 x4 x5 x6 x7
x6 ∞ ∞     ∞         x6 x0 x1 x2 x3 x4 x5 x6 x7
x7 ∞ ∞ ∞ ∞           x7 x0 x1 x2 x3 x4 x5 x6 x7
                                     
l3 x0 x1 x2 x3 x4 x5 x6 x7   n3 x0 x1 x2 x3 x4 x5 x6 x7
x0               ∞   x0 x0 x1 x1 x3 x2 x2 x2 x7
x1               ∞   x1 x0 x1 x2 x2 x2 x2 x2 x7
x2               ∞   x2 x1 x1 x2 x3 x4 x5 x6 x7
x3               ∞   x3 x0 x2 x2 x3 x2 x2 x6 x7
x4                   x4 x2 x2 x2 x2 x4 x5 x2 x7
x5                   x5 x2 x2 x2 x2 x4 x5 x6 x7
x6                   x6 x2 x2 x2 x3 x2 x5 x6 x7
x7 ∞ ∞ ∞ ∞           x7 x0 x1 x2 x3 x4 x5 x6 x7
                                     
l4 x0 x1 x2 x3 x4 x5 x6 x7   n4 x0 x1 x2 x3 x4 x5 x6 x7
x0               ∞   x0 x0 x3 x3 x3 x3 x3 x3 x7
x1               ∞   x1 x3 x1 x2 x2 x2 x2 x2 x7
x2               ∞   x2 x3 x1 x2 x3 x4 x5 x6 x7
x3               ∞   x3 x0 x2 x2 x3 x2 x2 x6 x7
x4                   x4 x3 x2 x2 x2 x4 x5 x2 x7
x5                   x5 x3 x2 x2 x2 x4 x5 x6 x7
x6                   x6 x3 x2 x2 x3 x2 x5 x6 x7
x7 ∞ ∞ ∞ ∞           x7 x0 x1 x2 x3 x4 x5 x6 x7
                                     
l5 x0 x1 x2 x3 x4 x5 x6 x7   n5 x0 x1 x2 x3 x4 x5 x6 x7
x0                   x0 x0 x3 x3 x3 x3 x3 x3 x4
x1                   x1 x3 x1 x2 x2 x2 x2 x2 x4
x2                   x2 x3 x1 x2 x3 x4 x5 x6 x4
x3                   x3 x0 x2 x2 x3 x2 x2 x6 x4
x4                   x4 x3 x2 x2 x2 x4 x5 X2 x7
x5                   x5 x3 x2 x2 x2 x4 x5 x6 x7
x6                   x6 x3 x2 x2 x3 x2 x5 x6 x7
x7                   x7 x4 x4 x4 x4 x4 x5 x6 x7
                                     
l6 x0 x1 x2 x3 x4 x5 x6 x7   n6 x0 x1 x2 x3 x4 x5 x6 x7
x0                   x0 x0 x3 x3 x3 x3 x3 x3 x4
x1                   x1 x3 x1 x2 x2 x2 x2 x2 x4
x2                   x2 x3 x1 x2 x3 x4 x5 x6 x4
x3                   x3 x0 x2 x2 x3 x2 x2 x6 x4
x4                   x4 x3 x2 x2 x2 x4 x5 x2 x7
x5                   x5 x3 x2 x2 x2 x4 x5 x6 x7
x6                   x6 x3 x2 x2 x3 x2 x5 x6 x7
x7                   x7 x4 x4 x4 x4 x4 x5 x6 x7
l7 x0 x1 x2 x3 x4 x5 x6 x7   n7 x0 x1 x2 x3 x4 x5 x6 x7
x0                   x0 x0 x3 x3 x3 x3 x3 x3 x4
x1                   x1 x3 x1 x2 x2 x2 x2 x2 x4
x2                   x2 x3 x1 x2 x3 x4 x5 x6 x4
x3                   x3 x0 x2 x2 x3 x2 x2 x6 x4
x4                   x4 x3 x2 x2 x2 x4 x5 x2 x7
x5                   x5 x3 x2 x2 x2 x4 x5 x6 x7
x6                   x6 x3 x2 x2 x3 x2 x5 x6 x7
x7                   x7 x4 x4 x4 x4 x4 x5 x6 x7

По матрицам ||l7|| и ||ni,j7|| можно найти длину кратчайшего перехода между любой парой вершин исходного графа.

Например, между вершинами х0 и х7 длина кратчайшего пути равна 18, а переход n07=(х0, х3, х2, х4, х7), между вершинами х1 и х6 длина кратчайшего пути равна 8, а переход n16=(х1, х2, х6) и т.д.

При решении практических задач возникает необходимость поиска нескольких путей, частично - упорядоченных по возрастанию относительно кратчайшего. Такие задачи возникают при временной загруженности канала на определенном участке или неисправности узла. Для решения подобных задач разработаны обобщенные алгоритмы Флойда.
Поделиться:





Воспользуйтесь поиском по сайту:



©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...