 |
Поиск дополнительного графа
|
|
|
|
Для формирования дополнительного графа ùG=<X,`r> необходимо найти дополнение отношения r по матрице смежности графа G=<X, r>:
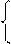1, если r(i, j)=0,
`r(i, j)=
0, если r(i, j)=1
и построить граф, опираясь на исходное множество вершин.
На рис. 3.4 дан граф и его дополнение. Ниже приведены матрица смежности графа G и матрица смежности графаùG.
| r | x1 | x2 | x3 | x4 | x5 | `r | x1 | x2 | x3 | x4 | x5 | |
| x1 | x1 | |||||||||||
| x2 | x2 | |||||||||||
| x3 | x3 | |||||||||||
| x4 | x4 | |||||||||||
| x5 | x5 |
Введение и удаление вершин графа
Если добавить вершину xi в граф G=<X, r>, то для каждой новой вершины следует найти все инцидентные ей ребра (xi, x), где xÎX. Для этого удобно использовать матрицу инциденции, каждая строка которой для контроля содержит ровно две “1”. В результате получен новый граф G’=<X’, r’>, где X'=XÈxi, r’=rÈ{(xi, x)}.
Если необходимо удалить хотя бы одну вершину xi графа G=<X, r>, то следует удалить все ребра, инцидентные данной вершине. Для этого также удобно использовать матрицу инциденции, каждая строка которой для контроля содержит ровно две “1”. В результате будет получен новый граф G’=<X’, r’>, где X'=X\xi, r’=r\{(xi, x), xÎX }.
Стягивание вершин графа
Если G=<X, r> содержит клику G1=<X1, r1>, где X1ÍX, r1Ír, то можно заместить G1 вершиной xa и получить граф G'=<X’, r’>, где X’=xaÈX\X1 и r’={r(xs, xa), где xsÎX\X1}È
Èr\{r1Èr(xt, xs), где xtÎX1 и xsÎX\X1}.
Если в графе G'=<X’, r’> необходимо вершину xa размножить {xb}ÏX’, то будет сформирован граф G=<X, r>, где
|
|
|
X=X’È{xb} и r=r’È{(x’, xb), где x’ÎX’\xa}È{(xbi, xbj), где xbi, xbjÎ{xb}}.
Пример: на рис. 3.15а) дан граф G, а на рис. 3.15b) граф G’. Выполнить стягивание клики G1 в вершину xa и замену вершины xa кликой G1.
| r | x1 | x2 | x3 | x4 | x5 | x6 | r’ | x1 | x2 | x3 | xa | |
| x1 | x1 | |||||||||||
| x2 | x2 | |||||||||||
 x3
| x3 | |||||||||||
| x4 | xa | |||||||||||
| x5 | ||||||||||||
| x6 |
Введение и удаление ребер графа
Если удалить ребро (xi, xj) графа G=<X, r>, где xi, xjÎX, то не следует удалять инцидентные данному ребру вершины. В результате будет получен новый граф G’=<X’, r’>, где X’=X, r’=r\(xi, x).
Если добавить ребро (xi, xj) в граф G=<X, r>, где xi, xjÎX, то удобно использовать матрицу инциденции, каждая строка которой для контроля содержит ровно две “1”. В результате получен новый граф G’=<X’, r’>, где X'=X, r’=r\(xi, x).
Поиск плотности и неплотности графа
Для определения плотности графа достаточно вычислить матрицу достижимости ||q|| = IÈr и выполнить перестановки строк и столбцов так, чтобы найти блоки матрицы, описывающие клику графа.
Пусть дана матрица смежности ||r||,
| r | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 |
| q | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | Матрица достижимости ||q|| = IÈ||r|| формируется добавление ”1” на главной диагонали матрицы ||r||. В матрице достижимости есть три блока {x1, x2, x3}, {x3, x4, x5}, {x5, x6, x7}, отражающих три полных подграфа. |
| x1 | |||||||||
| x2 | |||||||||
| x3 | |||||||||
| x4 | |||||||||
| x5 | |||||||||
| x6 | |||||||||
| x7 | |||||||||
| x8 |
Однако, если выполнить перестановки строк и столбцов матрицы (это может быть повторено n! раз), то будет найден блок, опирающийся на четыре вершины. Например, {x1, x3, x5, x7}.
|
|
|
| x1 | x3 | x5 | x7 | x2 | x4 | x6 | x8 | |
| x1 | ||||||||
| x3 | ||||||||
| x5 | ||||||||
| x7 | ||||||||
| x2 | ||||||||
| x4 | ||||||||
| x6 | ||||||||
| x8 |
Следовательно, r(G)=4. См. граф на рис. 3.14.
Для определения неплотности графа необходимо найти дополнительный граф G=<X, `r>, определить для него матрицу достижимости ||q-||=IÈ||`r|| и выполнить необходимое число перестановок строк и столбцов, чтобы найти блоки, опирающиеся на наибольшее число вершин. Для графа, приведенного на рис. 3.14 найдем матрицу ||`r|| дополнительного графа и матрицу достижимости ||q-||=IÈ||`r||. Для данного графа ||r|| = ||q||.
| `r | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 |
В результате перестановок строк и столбцов получено два блока: {x2, x4, x6, x8}, (x7, x2, x4}. Число вершин в одном из них равно четырем. Следовательно, r(ùG)=e(G)=4.
| q- | x1 | x3 | x5 | x7 | x2 | x4 | x6 | x8 |
| x1 | ||||||||
| x3 | ||||||||
| x5 | ||||||||
| x7 | ||||||||
| x2 | ||||||||
| x4 | ||||||||
| x6 | ||||||||
| x8 |
|
|
|
