 |
I. Определение количества силовых участков
|
|
|
|
Силовой участок – это участок вала между двумя внешними моментами.
Для определения величины неизвестного момента Х выразим угол поворота свободного конца (сечение А) через действующие моменты и приравняем его нулю.
Для этого применим принцип независимости действия сил, который для нашего случая формулируется так: для того, чтобы вычислить угол поворота 
от группы моментов нужно вычислить этот угол от каждого сосредоточенного момента, действующего отдельно, и все результаты алгебраически сложить.
При действии только сосредоточенного момента Х кручению подвергаются все участки вала. Используя (2.10) получим
При действии только момента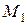 
кручению подвергается четвертый участок – поворачивается сечение D, а вслед за ним на тот же угол поворачивается остальные участки без деформации 
.
Таким же путем находим
; 
.
Окончательно,
.
;
Учтем, что 
при 
Умножив обе части расчетного уравнения на 
, получим
II. Построение эпюры крутящих моментов с учетом Х
Определим крутящий момент на каждом силовом участке, применив метод сечений:
Мкр 1 = X = 1,06 кНм;
Мкр 2 = Х – М 3 = 1,06 – 2,2 = –1,14 кНм;
Мкр 3 = Х – М 3 + М 2 = 1,06 – 0,1 = 1,05 кНм;
Мкр 4 = Х – М 3 + М 2 – М 1 = 1,06 – 2,1 = –1,04 кНм.
По полученным значениям крутящих моментов строим эпюру Мкр (рис. 6,б).
III. Определение размеров поперечных сечений вала
Расчет на прочность
На участках I и IY круглые поперечные сечения одинаковые с диаметром 
. Наиболее опасным из этих двух участков является участок I 
.
На участках II и III – сечение диаметром 
. Наибольший по модулю момент 
на участке II.
Таким образом, для всего вала опасным по прочности является I участок.
Находим диаметр из условия прочности 
|
|
|
Отсюда 
Расчет на жесткость
Выражаем относительные углы закручивания через .
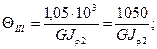
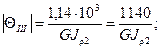
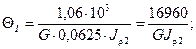
Следовательно, на первом участке имеет место максимальный угол закручивания.
По условию жесткости, переведя градусы в радианы, получим
Из условий прочности и жесткости 
. Округляем до целых мм: 
, отсюда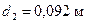 
IV. Построение эпюр касательных напряжений t в поперечных
сечениях вала (рис.7)
Сечение I-I
Сечение II-II
Сечение III-III
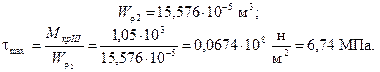
Сечение IY-IY
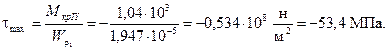
Рис.9
Y. Построение эпюры узлов поворота сечений вала
Полярные моменты инерции сечений для:
участков I и IY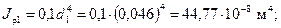 
участков II и III 
Жесткость сечений на кручение
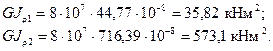
Углы поворота отдельных сечений вала определяются по отношению к неподвижному сечению (в нашем случае жесткая заделка) 
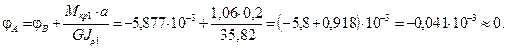
Ошибка составляет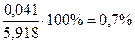 
.
По вычисленным значениям 
строим эпюру углов закручивания (рис. 6,в). Так как крутящие моменты на всех участках постоянны, то ординаты эпюры углов закручивания линейно зависят от координаты Z – расстояние от начала участка до сечения
ИЗГИБ БАЛОК
Простым изгибом называется такое нагружение стержня, когда все силы (в том числе и опорные реакции) направлены перпендикулярно оси стержня и лежат в одной из его главных плоскостей инерции (рис.1). Стержень, работающий на изгиб, называется балкой.
рис. 1
Для того, чтобы балка могла сопротивляться действию внешней нагрузки, она, как правило, должна быть соответствующим образом закреплена. Обычно используются три вида опорных закреплений:
1. Шарнирно подвижная опора (рис.2а)
Эта опора препятствует перемещению балки по вертикали, и разрешает горизонтальное смещение и поворот сечения. Следовательно, по вертикали на схеме рисуется абсолютно недеформируемый опорный стержень между двумя шарнирами и соответствующая опорная реакция.
2. Шарнирно неподвижная опора (рис.2б)
Эта опора препятствует линейному перемещению балки в любом направлении. На схеме показывают два опорных стержня между шарнирами, образующими жесткий треугольник. Неизвестный заранее вектор опорной реакции заменяют его составляющими по осям.
|
|
|
3. Жесткое защемление (заделка) (рис.2в)
Невозможны линейное перемещение сечения и поворот. На схеме показывают составляющие вектора реакции и реактивный момент. Заделку можно моделировать постановкой трех связей.
Комбинируя различные типы закреплений, можно получить ряд схем балок:
1. Балка шарнирно опертая по концам (рис.3а)
Одна опора шарнирно подвижная, другая – шарнирно неподвижная. Расстояние между центрами опор на схеме называется пролетом. Число реакций равно трем.
Учитывая, что для плоской системы сил можно составить три независимых уравнения равновесия системы в целом, приходим к заключению, что балка статически определимая.
2. Балка шарнирно опертая с консолями (С1 и С2) (рис.3б)
Реакции те же. Балка статически определимая.
3. Балка жестко закрепленная одним концом (рис.3в)
В заделке три реакции. Балка статически определимая. При действии нагрузки перпендикулярной оси реакция НВ всегда равна 0.
Внутренние силовые факторы в сечении изгибаемой балки
Рассмотрим для простоты балку с прямоугольным поперечным сечением (рис.4). Следуя методу сечений, мысленно проведем разрез и отбросим какую-либо часть балки, а другую оставим. На оставшейся части покажем действующие на нее силы и в поперечном сечении – внутренние силовые факторы, которые являются результатом приведения к центру сечения сил, действующих на отброшенную часть. Учитывая, что внешние силы и распределенные нагрузки лежат в одной плоскости и действуют перпендикулярно оси балки, в сечении получим поперечную силу Qy и изгибающий момент Мх. Эти внутренние силовые факторы заранее неизвестны, поэтому их показывают в положительном направлении в соответствии с принятыми правилами знаков.
рис. 2
рис. 3
Поперечная сила Qy считается положительной, если при взгляде на оставшуюся часть она стремится вращать эту часть относительно ближайшей точки на оси балки по часовой стрелке.
рис. 4
Изгибающий момент считается положительным, если он стремится изогнуть балку выпуклостью вниз.
|
|
|
На рис.4 показаны два случая оставшейся части: левая и правая.
Для определения величины Qy и Мх составляются два уравнения равновесия для оставшейся части
Уравнение момента составляется относительно оси Х, проходящей в поперечном сечении через точку на оси балки – тогда поперечная сила в уравнение не входит и величина Мх определяется независимо от Qy. Можно доказать, что результат вычислений Qy и Мх не зависит от того, равновесие какой оставшейся части рассматривается.
Результаты вычислений Qy и Мх показываются в виде эпюр. При этом ординаты эпюры Qy откладывают как в обычном графике в курсе математики – плюс вверх, минус вниз, а ординаты эпюры Мх в строительных отраслях и в железнодорожных расчетах принято откладывать в сторону выпуклости балки и знак не ставить.
Между ординатами эпюр Qy, Мх и q (функций от координаты z) существуют дифференциальные зависимости. Рассмотрим балку, загруженную распределенной нагрузкой, меняющейся по длине по закону qz (рис.5а). Выделим кусок балки длиной dz у сечения на расстоянии z от начала координат (рис.5б), и рассмотрим его равновесие:
Отсюда
(1)
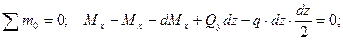
рис. 5
Отсюда, пренебрегая бесконечно малыми величинами второго порядка малости, получим
. (2)
Дифференцируя обе части равенства (2) по z и учитывая (1), будем иметь
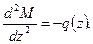(3)
Напряжения в сечении изгибаемой балки
Рассмотрим балку, показанную на рис. 6. На участках АС и ДВ поперечная сила постоянная, а изгибающий момент изменяется. На участке СД поперечная сила равна 0, а изгибающий момент постоянный – такой случай называется чистым изгибом. В общем случае в любой точке поперечного сечения возникают два вида напряжений - нормальное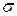 
и касательное 
(рис.7). Они связаны с внутренними силовыми факторами соотношениями эквивалентности:
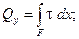(4)
(5)
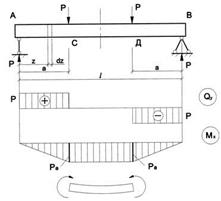
рис. 6
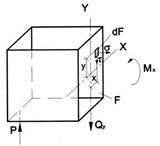
рис. 7
Значения Qy и Мх можно определить методом сечений, рассматривая равновесие оставшейся части. Задача состоит в определении законов действительного распределения 
в поперечном сечении, удовлетворяющих уравнениям (4) и (5). Эта задача статически неопределимая. Для ее решения следует рассмотреть деформации балки при изгибе.
|
|
|
Нормальные напряжения при изгибе
Рассмотрим для наглядности резиновую балку с нарисованной на ее поверхности до деформации системой взаимно перпендикулярных линий (рис.8а) в условиях чистого изгиба. Линии параллельные оси станут дугами окружностей, а линии перпендикулярные оси станут отрезками радиусов (рис.8б). Рассматривая картину деформации можно высказать несколько гипотез:
рис. 8
1. Гипотеза плоских сечений: сечения плоские до деформации (след этих сечений представляет линии перпендикулярные оси) остаются плоскими (след в виде отрезков радиусов) после деформации, но поворачиваются относительно друг друга.
2. Длина отрезка mk в направлении перпендикулярном оси до деформации и 
не изменяется, поэтому высказывается гипотеза о том, что продольные слои балки (иногда их называют волокнами) друг на друга не давят в поперечном направлении.
3. Длина отрезка ab сократилась, а отрезка cd увеличилась. Следовательно, в верхней части балки волокна сжимаются, а в нижней растягиваются. Значит, по высоте балки существует слой, который не сжимается и не растягивается – нейтральный слой. Поместим на этом слое начало координат в поперечном сечении. Ось Х будет лежать в сечении перпендикулярно оси симметрии Y. Назовем ось X нейтральной осью.
Покажем бесконечно малый участок dz балки до и после деформации нарисованный в соответствии с гипотезами (рис.9). Рассмотрим отрезок 1-2. После деформации он станет дугой окружности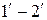 
радиуса 
Здесь 
- радиус кривизны нейтрального слоя. Учитывая принятую гипотезу, о ненадавливании волокон друг на друга, можно считать,что волокно 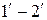работает на растяжение, и справедлив закон Гука, связывающий относительную деформацию и нормальное напряжение
. (6)
рис. 9
Найдем относительную деформацию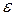 
волокна 1-2
Вычитая, получим абсолютную деформацию
(7)
Теперь 
(8)
Учитывая, что при 
волокна сжимаются, вместо (8) и (6) будем иметь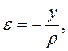 
(9)
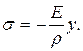(10)
При изгибе нормальная сила равна нулю. С другой стороны она связана с нормальными напряжениями соотношением эквивалентности
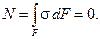(11)
Подставим (10) в (11), тогда получим
(12)
Отсюда 
, но интеграл слева – это статический момент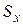 
площади поперечного сечения балки относительно нейтральной оси Х. Известно, что если 
, то ось Х проходит через центр тяжести. Следовательно, при изгибе нейтральный слой проходит через центр тяжести. Теперь ясно, откуда откладывать y в (10).
Для определения кривизны балки 
подставим (10) в (5)
(13)
Отсюда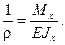 
(14)
|
|
|
Здесь введем обозначение: 
- момент инерции сечения относительно нейтральной оси. Величина характеризующая геометрию сечения с размерностью 
.
Для прямоугольника (рис. 10а) 
(15)
Для круга (рис.10б) 
(16)
Для прокатных двутавровых профилей (рис. 10в) величина 
дается в таблицах сортамента (см. приложение 1) в зависимости от номера, который численно равен высоте двутавра 
в см.
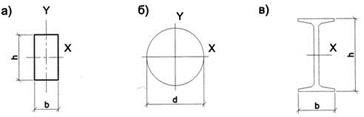
рис. 10
Подставляя (14) в (10), получим формулу нормальных напряжений при чистом изгибе 
(17)
В инженерных расчетах знак минус в формуле не ставят, все величины берут по модулю, а знак напряжения учитывают по характеру действия изгибающего момента – где выпуклость, там растяжение и наоборот.
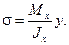(18)
Напряжения 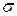зависят от расстояния точки до нейтральной оси и не зависят от координаты Х (рис.11).
Наибольшие по величине нормальные напряжения возникают в точках поперечного сечения наиболее удаленных от нейтральной оси Х
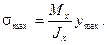(19)
Обычно вводится геометрическая величина в (м3) 
(20)
рис. 11
Тогда формулу для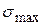 
можно записать в виде 
Для прямоугольника 
(21)
Для круга 
(22)
Для двутавра 
приводится в таблицах сортамента (см. приложение 1).
Учитывая, что волокна балки испытывают деформации растяжения или сжатия, можно записать условие прочности
(23)
где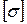 
- допускаемое напряжение для данного материала (см. раздел «Растяжение-сжатие).
Из условия (23) формулируют три рода задач на прочность при изгибе:
1. Проверка прочности: задана балка, нагрузка, известен материал. Строится эпюра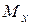 
- определяется 
, вычисляется и по (23) проверяется условие прочности.
2. Определение максимально допустимой нагрузки по условию прочности.
(24)
Заданы размеры балки, характер нагрузки, материал балки.
Строится эпюра 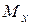- определяется от параметра нагрузки, вычисляется и по (24) находят наибольший параметр нагрузки.
3. Конструирование балки – определение размеров ее поперечного сечения.
(25)
Строится эпюра 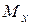- определяется , вычисляется правая часть (25) и подбираются размеры поперечного сечения, удовлетворяющие (25).
Для прямоугольного сечения 
Обычно задаются отношением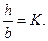 
(26)
Тогда 
отсюда 
. (27)
Задаваясь шириной 
по (26) получим .
Для двутаврового сечения по таблице сортамента (см. приложение 1) подбирают номер двутавра с большим, чем правая часть (25).
Касательные напряжения при изгибе
Выделим бесконечно малый кусок балки на участке АС (рис.6), где поперечная сила постоянная и рассмотрим его равновесие. Сечение балки примем в виде узкого прямоугольника (рис.12).
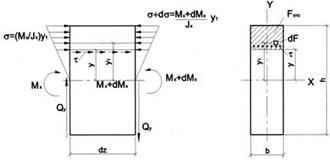
рис. 12
В сечении на расстоянии 
от опоры действует изгибающий момент 
а в сечении на расстоянии 
действует момент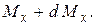 
Поэтому и нормальные напряжения в правом сечении больше, чем на том же уровне в левом сечении. Мысленно отсечем верхнюю часть горизонтальным сечением и рассмотрим ее равновесие. Видно, что равнодействующая нормальных напряжений справа будет больше, чем слева. Для восстановления равновесия можно предположить, что по горизонтальному сечению действуют касательные напряжения , удерживающие верхнюю отсеченную часть от смещения вдоль оси 
.
Русский инженер Д.И. Журавский высказал гипотезу о равномерном распределении касательных напряжений по горизонтальному сечению – она справедлива, если «» мало по сравнению с высотой сечения.
Запишем уравнение равновесия для отсеченной части:
(28)
Здесь использовано дифференциальное соотношение (2)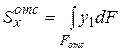 
- статический момент отсеченной части площади относительно нейтральной оси Х.
Если толщина не меняется, то наибольшие касательные напряжения будут на нейтральной оси.
Для двутавра
где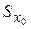 
- статический момент половины поперечного сечения относительно нейтральной оси. Его значение приводится в таблицах сортамента.
Проверка прочности по касательным напряжениям проводится в сечениях балки с максимальным 
на уровне нейтральной оси.
(29)
где 
- допускаемое касательное напряжение, оно, как правило, равно половине .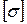
|
|
|
