Статически определимых балок

Такое нагружение характерно для валов механизмов, передающих мощность от источника к приемнику с помощью ременных и зубчатых передач (рис.6).

Перенесем действующие силы в центры тяжести соответствующих сечений и разложим их на составляющие по осям X и Y. При переносе, кроме сил, перпендикулярных оси вала, должны быть учтены крутящие моменты.

рис. 6

 

рис. 7

 

Применяя принцип независимости действия сил, построим эпюры изгибающих моментов и эпюру крутящих моментов .

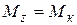Таким образом, в любом поперечном сечении вала возникают два изгибающих и один крутящий момент.

Рассмотрим напряжения, возникающие в сечении вала отдельно от изгиба и кручения.

Если в сечении возникают два изгибающих момента относительно главных центральных осей, то такой случай называется косым изгибом. Изгибающие моменты связаны с нормальными напряжениями 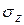, направленными перпендикулярно плоскости поперечного сечения (рис.7) и зависящими от координаты точки, в окрестности которой они действуют.

При выводе формулы для будем считать, что изгибающий момент положительный, если он вызывает растягивающие напряжения 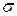в первом квадрате поперечного сечения.

Используем принцип независимости действия сил – от каждого изгибающего момента напряжения определяются по формуле для плоского изгиба, а затем складываются (2.1)

Величина нормального напряжения линейно зависит от координат X и Y точки, в окрестности которой оно определяется. Поэтому вершины стрелок напряжений лежат на плоскости (плоскости напряжений), наклоненной к плоскости поперечного сечения. Как известно, две плоскости пересекаются по прямой линии. В нашем случае это будет линия, в точках которой т.е. нулевая линия.

Таким образом, уравнение нулевой линии имеет вид

(2.2)

Нулевая линия при косом изгибе проходит через центр тяжести сечения (точка X=0, Y=0 удовлетворяет уравнению (2.2)) и составляет с осью X угол (рис.7).

На рис.7 линия обозначена индексами .

Из уравнения (2.2) получим (2.3)

так как для круглого сечения .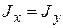

Плоскость напряжений имеет наибольшую высоту по сравнению с плоскостью поперечного сечения в точках, наиболее удаленных от нулевой линии, т.е. в точках пересечения диаметра, перпендикулярного к нулевой линии с внешней окружностью (точки А и В). Для вычисления максимального нормального напряжения в точке А воспользуемся формулой (2.1).

(2.4)

где - радиус круга.

(2.5)

Отношение момента инерции относительно оси к наибольшему расстоянию точки поперечного сечения от этой оси называется моментом сопротивления 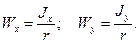(2.6)

Теперь (2.5) можно записать в виде

(2.7)

Выразим через

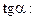
(2.8)

причем учитывается по модулю.

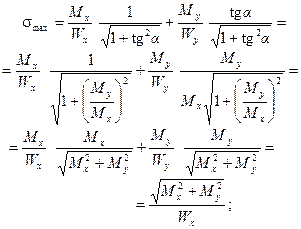(2.9)

Введем обозначения 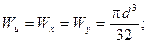(2.10)

(2.11)

Таким образом, (2.12)

Формулу (2.12) можно получить и другим способом. Учтем, что для круглого сечения все центральные координаты оси в плоскости сечения являются равноценными и являются главными центральными осями. Поэтому можно найти плоскость, в которой будет действовать суммарный изгибающий момент

Для его определения представим действующие изгибающие моменты в виде векторов. Будем считать, что при взгляде из вершины вектора момент должен быть виден вращающим против часовой стрелки (рис.8).

Суммарный вектор найдем сложением векторов .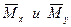

Модуль вектора . (2.13)

Плоскость действия суммарного момента перпендикулярна вектору . Теперь напряжение в точке А определяется по формуле простого изгиба

 

рис. 8

 

При кручении в плоскости поперечного сечения в окрестности каждой точки действуют касательные напряжения (2.14)

которые у края поперечного сечения достигают максимального значения

(2.15)

где полярный момент сопротивления - 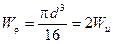. (2.16)

Таким образом, в поперечном сечении в окрестности точки А действует кроме максимального нормального напряжения и максимальное касательное напряжение

На рис.9 показан бесконечно малый параллелепипед у точки А с действующими по его граням напряжениями. Направление совпадает с направлением . По наружной площадке напряжения равны нулю.

рис. 9

 

Таким образом, стрелки напряжений лежат в одной плоскости – такое напряженное состояние называется плоским напряженным состоянием (рис.10). При деформации стержней всегда возникает плоское напряженное состояние с одной парой нормальных напряжений по исходным площадкам.

Если в окрестности точки А выделить бесконечно малый параллелепипед, повернутый по отношению к исходному, то напряжения по его граням изменятся по величине и направлению. В курсе «Сопротивление материалов» доказывается, что существует такое положение параллелепипеда, когда по его граням касательные напряжения будут равны нулю, и будут действовать только нормальные напряжения, которые называются главными напряжениями.

рис. 10

Если в окрестности точки А выделить бесконечно малый параллелепипед, повернутый по отношению к исходному, то напряжения по его граням изменятся по величине и направлению. В курсе «Сопротивление материалов» доказывается, что существует такое положение параллелепипеда, когда по его граням касательные напряжения будут равны нулю, и будут действовать только нормальные напряжения, которые называются главными напряжениями.

Главные напряжения определяются по формуле

(2.17)

а направление – по формуле (2.18)

Главные максимальные напряжения всегда действуют в квадрантах, где сходятся стрелки касательных напряжений .

При плоском напряженном состоянии прочность оценивается с помощью так называемых теорий (гипотез) прочности. Исторически было высказано несколько гипотез о причине разрушения материалов. В машиностроении применяется так называемая третья теория прочности. Согласно которой разрушение в окрестности точки наступает в тот момент, когда величина наибольших касательных напряжений достигает для заданного материала опасного значения определенного в опытах при растяжении и сжатии. Эти напряжения действуют по площадкам, наклоненным к главным площадкам под углом 45⁰ и равны

(2.19)

Таким образом, условие прочности по третьей теории будет иметь вид

но при растяжении поэтому окончательно

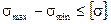(2.20)

Подставляя в (2.20) главные напряжения из (2.17), получим

(2.21)

(2.22)

Учитывая (2.13), будем иметь

(2.23)

Обозначим - приведенный момент. (2.24)

Таким образом, вал рассчитывается по формуле похожей на формулу проверки прочности при изгибе (2.25)

но учитывается приведенный момент (2.24).

Из условия прочности, учитывая (2.10), получим

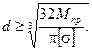(2.26)

ЗАДАЧА 6

 

При вычислении напряжений в случае внецентренного растяжения или сжатия следует определить положение главных центральных осей инерции поперечного сечения бруса. Все значения координат точки приложения силы и точек, в которых определяются напряжения, отсчитываются от главных центральных осей инерции.

Необходимо при этом научиться определять положение нулевой линии для различных поперечных сечений бруса и для разных точек приложения продольной силы.

Выполнение данной задачи содействует приобретению знаний по теории расчета внецентренно сжатых брусьев. Рекомендуется перед решением данной задачи знать формулу для определения нормального напряжения в любой точке сечения бруса, понятие о ядре сечения и метод его построения.

Пример

На брус заданного поперечного сечения в точке D верхнего торца действует продольная сжимающая сила Р =300 кН (рис.11). Требуется найти положение нулевой линии, определить наибольшие (растягивающие и сжимающие) напряжения и построить ядро сечения.

Решение:

1. Нахождение положения главных центральных осей инерции и определение площади поперечного сечения

Так как поперечное сечение бруса (рис.11) имеет две оси симметрии, а они всегда проходят через центр тяжести сечения и являются главными, то главные центральные оси сечения х _с и у_с будут совпадать с этими осями симметрии.

Центр тяжести сечения С в этом случае определять не надо, так как он совпадает с геометрическим центром сечения.

Площадь поперечного сечения бруса равна:

 

рис. 11

 

Площадь поперечного сечения бруса равна:

2. Определение главных центральных моментов инерции и главных радиусов инерции

Моменты инерции определяем по формулам:

Вычисляем квадраты главных радиусов инерции:

 

3. Определение положения нулевой линии

Отрезки, отсекаемые нулевой линией на главных центральных осях инерции, определяем по формулам:

где х_р =2,3 см и у_р =2 см – координаты точки приложения силы Р (точка Р рис.11). Отложив отрезк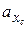и и 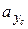соответственно на осях х_с и у_с и проводя через их концы прямую, получим нулевую линию сечения, на которой нормальные напряжения равны нулю (). На рис.11 эта линия обозначена n-n.

 

3. Определение наибольших сжимающих и растягивающих напряжений и построение эпюры напряжений

Точка D, координаты которой х_D =5,25 см и у_D =5 см, наиболее удалена от нулевой линии в сжатой зоне сечения, поэтому наибольшие сжимающие напряжения возникают в ней и определяются по формуле

Наибольшие растягивающие напряжения возникают в точке К, имеющей координаты х_к = ‑5,25 см, у_к = ‑5 см.

По полученным значениям s_D и s_K строим эпюру нормальных напряжений (см. рис.11).

5. Построение ядра сечения

Для построения ядра сечения, учитывая, что сечение симметричное, рассмотрим два положения касательной к контуру сечения I-I и II-II(см. рис.11).

Отрезки, отсекаемые касательной I-Iна осях координат, равны:

Координаты граничной точки 1 ядра сечения определяются по формулам:

Касательная II-II отсекает отрезки 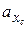=5,25 см, 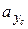=¥. Координаты граничной точки 2:

Координаты граничных точек второй половины ядра сечения можно не определять, так как сечение бруса симметричное. Учитывая это для касательных III-III и IV-IV, координаты граничных точек 3 и 4 будут:

 

= 0; = 15,2×10^-3 м;

= 23,0×10^-3 м 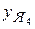= 0.

 

Соединив последовательно точки 1, 2, 3 и 4 прямыми получим ядро сечения (рис.11).

 

ЗАДАЧА 7

Стальной вал постоянного сечения (рис.12,а) вращается с частотой n об/мин и передает мощность N кВт. Подобрать диаметр вала, если заданы предел текучести материала и запас прочности .

рис. 12

Числовые данные к задаче: а = 0,3 м; b = 0,3 м; c = 0,2 м; D ₁ = 0,3 м; D ₂ = 0,6 м; N = 20 кВт; n ₁ = 120 об/мин; материал Ст50; = 300 МПа; запас прочности по отношению к пределу текучести .

Решение:

1. Определение нагрузок, передающихся на вал

1.1. Определение крутящего момента по формуле

1.2. Определение окружных усилий по формулам и разложение их на вертикальную и горизонтальную составляющие

Выполняем вычисления и показываем все найденные силы на расчетной схеме вала (рис.12,б)

 

2. Построение эпюр моментов

2.1. Построение эпюры крутящих моментов

Эпюра крутящих моментов располагается между шкивами, т.к. скручивается только этот участок вала. Величина крутящего момента определена в п.1.1.: =1,60 кНм (рис.12,в)

2.2. Построение эпюры изгибающих моментов относительно осей Х – М_х изгиб вертикальной плоскости

Схема нагрузок показана на рис. 12,г.

Находим опорные реакции

 

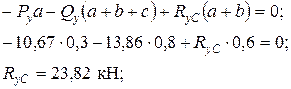
Проверка:

Точность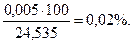

Вычисляем моменты в характерных точках:

По вычисленным значениям моментов строится эпюра (рис.12,д).

2.3. Построение эпюры изгибающих моментов 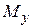(изгиб в горизонтальной плоскости)

Схема нагрузок, действующих в этой плоскости, показана на рис.12,е).

Находим опорные реакции:

Проверка:

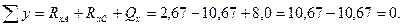
Вычисляем моменты в характерных точках:

По найденным значениям строится эпюра изгибающих моментов в горизонтальной плоскости 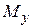(рис. 12,ж).

 

3. Подбор сечения (определение диаметра вала)

Материал Ст50, =380 МПа, запас =3.

Находим допускаемое напряжение:

Опасным в данном случае является сечение С, так как в этом сечении все моменты наибольшие, что видно по эпюрам. Выписываем величины моментов в сечении С:

Вычисляем приведенный расчетный момент:

По формуле (2.26) вычисляем диаметр вала:

 

 

В контрольной работе №4 решаются задачи, относящиеся к трем разделам курса «Сопротивление материалов».

Задача № 8 относится к разделу «Продольный изгиб стержней», задача № 9 – к разделу «Динамическое действие сил» и задача № 10 – к разделу «Переменные напряжения».

В каждом разделе установлена своя нумерация формул. Нумерация рисунков общая для всего текста.

 

1 ПРОДОЛЬНЫЙ ИЗГИБ СТЕРЖНЕЙ

Рассмотрим стержень длиной l (рис.1), сжимаемый силой Р. Заданы размеры поперечного сечения, известен материал, из которого изготовлен стержень.

рис 1.

Теоретически, при центральном сжатии в сечении стержня должны появиться нормальные сжимающие напряжения, равномерно распределенные по площади сечения. Это будет иметь место в идеальном случае: ось стержня идеально прямая, сила приложена точно в центре тяжести сечения и направлена по оси, отсутствуют воздействия, направленные поперек оси стержня.

На практике идеального нагружения достичь невозможно – всегда будут иметь место малые возмущения, изгибающие стержень с самого начала. Это могут быть малые отклонения оси от идеальной прямой, воздействие температуры, поперечное воздействие ветра или их сочетания, предусмотреть которые заранее невозможно.

Проектировщик должен быть убежден, что состояние сжатия от малых возмущений резко не изменится – оно будет устойчиво к этим возмущениям.

Оказывается, что если сжимающая сила меньше определенного значения, называемого критическим, то малые возмущения приводят к малым отклонениям стержня от прямой, и, если возмущения исчезают, то стержень возвращается в исходное сжатое состояние, если же возмущения не исчезают, то вызванные ими отклонения несущественны. В этом случае обеспечена устойчивость центрального сжатия. Но, если сжимающая сила достигнет критического значения, то действие малых возмущений становится существенно заметным – стержень получает большие отклонения оси от проектной прямой, т. е. становится сжато-изогнутым и не возвращается в исходное состояние после исчезновения возмущения. Это явление называют потерей устойчивости центрального сжатия или продольным изгибом.

Для длинных стержней такое состояние наступает при сжимающих напряжениях меньших предела пропорциональности – в упругой стадии. Оно опасно для самого стержня, так как он не был рассчитан на действиедополнительного изгибающего момента, но более всего для конструкции, в состав которой он входит – потеря устойчивости одного стержня может быть причиной разрушения всей конструкции, так как в этот момент стержень внезапно выключается из состава конструкции – исчезает необходимая связь.

Сказанное выше определяет важность знания величины критической силы .

Рассмотрим стержень, шарнирно опертый по концам под действием сжимающей силы (рис.2) в момент потери устойчивости. Ось стержня искривляется – все точки перемещаются на величину .

рис. 2

 

Используем дифференциальное уравнение изгиба балки

. (1)

Учтем, что в осях на рис.2 - отрицательные значения, поэтому в (1) подставим

Перенесем все члены влево и обозначим

(2)

Тогда получим дифференциальное уравнение потери устойчивости центрально сжатого шарнирно опертого стержня (3)

Решение уравнения (3) имеет вид

(4)

где А и В – постоянные интегрирования, которые находятся из граничных условий:

(5)

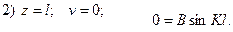(6)

Так как В ¹ 0 (не будет изгиба), то

(8)

Уравнение (7) является трансцендентным уравнением (неизвестное входит в аргумент тригонометрической функции). Это уравнение имеет множество корней .

Рассмотрим первое нетривиальное решение с минимальным Тогда из (2) следует (9)

Можно сказать, что рассматриваемый стержень теряет устойчивость по одной полуволне синусоиды, а В – амплитуда этого отклонения. Величина В зависит от конкретной причины (возмущения), вызывающей отклонения сжатого стержня от первоначально прямого положения, а так как возмущения не определенные, то и В остается неопределенной.

Для вычисления критических сил для стержней с другими закреплениями нужно рассматривать дифференциальное уравнение четвертого порядка. Но в курсе Сопротивления материалов поступают следующим образом: для каждого вида закреплений сравнивают длину между точками перегиба (с М=0) упругой линии при потере устойчивости (свободную длину ) с полуволной синусоиды l для шарнирно опертого стержня (рис.3) и вводят в (8) соответствующую свободную длину . (10)

Тогда, (11)

Формула Эйлера была выведена в предположении упругих деформаций, когда (рис.4) . (12)

Для закрепления одинаковых в двух главных плоскостях нужно брать минимальный момент инерции J _min.

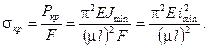
Здесь введено обозначение минимального радиуса инерции

Обычно вводится понятие максимальной гибкости стержня

(13)

Гибкость величины геометрическая. Теперь можно записать

(14)

Таким образом, формулу Эйлера для величины критической силы можно применить, если

рис. 3

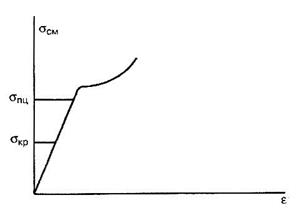
рис. 4

 

Отсюда можно найти условия для (15)

Введем обозначение для предельной гибкости (16)

Эта величина зависит от физически свойств материала стержня. Условие (15) перепишем в виде . (17)

Окончательно, если наибольшая гибкость больше предельной для данного материала, то стержень будет терять устойчивость при напряжениях меньше предела пропорциональности , а если условие (17) не удовлетворяется и , то стержень будет терять устойчивость при упруго-пластических деформациях, для которых дифференциальное уравнение (1) будет не справедливо.

В этом случае для критической силы применяется эмпирическая формула Ясинского-Тетмайера (18)

где а и в – коэффициенты, зависящие от материала и приводимые в справочниках.

При этом (19)

Таким образом, критические напряжения в любой стадии деформации зависят от гибкости : (20)

в упругой – по формуле (14) - гипербола Эйлера, в упруго-пластической – по формуле (19) – прямая Ясинского.

При некотором значении гибкости, которое можно обозначить через λ ₀, величина критических напряжений становится равной предельному напряжению сжатия (либо пределу текучести, либо пределу прочности). Это значение гибкости будет границей применимости формулы Ясинского. Таким образом, критические напряжения вычисляют по формуле Ясинского тогда, когда гибкость стержня меньше λ_пред, но не ниже λ ₀.

Если рассчитываемый стержень оказался малой гибкости λ < λ ₀, то опасность потери устойчивости меньше опасности разрушения, и такой стержень надо рассчитывать на прочность, а не на устойчивость.

Примерный вид графической зависимости критического напряжения от гибкости изображен на рис. 5.

Рис. 5

Для стержней большой гибкости λ ≥ λ_пред расчет ведется по формуле Эйлера, поэтому зависимость σ_кр от λ - гиперболическая (14). На графике это участок I, называемый гиперболой Эйлера.

Стержни средней гибкости λ ₀ ≥ λ > λ_пред рассчитываются по формуле Ясинского. Для них зависимость σ_кр от λ - линейная (19). Соответствующий участок II называется прямой Ясинского.

Для стержней малой гибкости нет надобности в расчете на устойчивость. Для них критическое напряжение считается постоянным и равным для пластичных материалов пределу текучести при сжатии, а для хрупких – пределу прочности при сжатии. На графике таким стержням соответствует участок III.

Вычислив гибкость стержня, и отложив ее на диаграмме, построенной для данного материала, определим, на какой участок диаграммы приходится λ, и в зависимости от этого производим расчет по нужной формуле.

В ряде случаев для подбора расчетных формул и самого расчета на устойчивость бывает весьма эффективным использовать справочные таблицы. Одна из таких таблиц приведена ниже.

Таблица 1

Материал	a, МПа	b, МПа	λ0	λпред
Сталь Ст.2, 15 Сталь Ст.3 Сталь Ст.5 Сталь 45 Дерево Д 16 Т	28,8	0,685 1,12 1,13 3,82 0,19 3,33	–

Вычислив значение σ_кр и умножив его на рассчитанную нами ранее площадь поперечного сечения стойки, получим величину критической силы P_кр:

P_кр = σ_кр F.

После этого можно, наконец, определить коэффициент запаса устойчивости

[ n_y ] = P_кр / P.

Инженерный расчет сжатых стержней на устойчивость формально можно поставить в соответствие расчету на простое сжатие, принимая в качестве допускаемого некоторую часть от критического напряжения:

σ = P / F ≤ [ σ_y ],

где [ σ_y ] = σ_кр / [ n_y ] - допускаемое напряжение на сжатие с учетом опасности продольного изгиба, или, иначе, допускаемое напряжение на сжатие при расчете на устойчивость.

Обычно [ σ_y ] выражают через основное допускаемое напряжение на сжатие для данного материала:

[ σ_y ] = φ [ σ_c ].

Здесь φ ≤ 1,0 - коэффициент понижения основного допускаемого напряжения на сжатие или коэффициент продольного изгиба; [ σ_c ] - основное допускаемое напряжение на сжатие, то есть установленное без учета продольного изгиба:

[ σ_c ] = σ_пред / [ n ].

 

Обычно под σ_пред для пластических материалов понимают σ_Т (предел текучести материала), а для хрупких – временное сопротивление σ_вр..

Связь между коэффициентом φ, критическим напряжением σ_кр, предельным напряжением σ_пред и коэффициентами запаса прочности [ n ] и устойчивости [ n_y ] можно установить следующим образом:

[ σ_y ] = φ [ σ_c ] = φ σ_пред / [ n ] = σ_кр /[ n_y ],

откуда, учитывая (20)

(21)

Величина коэффициента φ зависит от материала стержня и его гибкости. Некоторые значения φ по СНиП приведены в табл.9 заданий на контрольную работу и рекомендованы к использованию при решении данной задачи.

При выполнении расчетов на устойчивость по коэффициентам φ исходная зависимость имеет следующий вид:

. (22)

Из этого условия можно сформулировать три рода задач на устойчивость центрального сжатия (продольный изгиб).

 

Задача 1 рода. Проверка устойчивости

Дан стержень, известны условия закрепления, величина сжимающей нагрузки.

Алгоритм решения:

1. Определяется минимальный момент инерции относительно главных осей .

2. Вычисляется минимальный радиус инерции .

3. Вычисляется максимальная гибкость

4. По таблице определяем .

5. Проверяем условие (22), если оно удовлетворяется, то устойчивость обеспечена, если нет – не обеспечена с коэффициентом запаса, заложенным в табличном значении (см. (21)).

 

Задача 2 рода. Определение максимальной сжимающей нагрузки

(23)

Алгоритм тот же, но в п.5 используется формула (23).

 

Задача 3 рода. Конструирование стержня – подбор размеров поперечного сечения. В этом случае заранее неизвестны величины площади, моментов инерции и, следовательно, коэффициента .

Задача нелинейная. Ее решают методом последовательных приближений.

Алгоритм решения:

1. Задаются размерами поперечного сечения.

2. Выполняются действия с п.1 по п.5 алгоритма задачи первого рода.

Необходимо отметить, что наиболее рациональным с инженерно-экономической точки зрения будет такое сечение, для которого величина недогруза

не будет превышать 0,05 (или, что то же самое, 5 %). Таким образом, в случае, если в n -ом приближении неравенство (22) не выполняется, следует увеличить размеры поперечного сечения, в случае же, если δ >0,05, их следует уменьшить. В обоих случаях необходимо снова вернуться к определению λ _max и новому φ, для которого в очередной раз проверить справедливость условия устойчивости стойки (22).

Пример задачи № 8. Пусть стальная стойка высотой l =0,4 м сжимается силой P = 8,50 кН. Требуется подобрать коробчатое поперечное сечение с характерным размером a (рис. 6.2).

1. Определим моменты инерции сечения[2] относительно координатных осей x и y. Очевидно, что

I_x = BH³ / 12 – bh³ / 12, I_y = HB³ / 12 – hb³ /12.

Подставляя в эти выражения значения B, H, b и h,получим следующие формулы:

I _x = 100 a ⁴ /12, I _y =190 a ⁴ /12.

 

Легко видеть, что I _x < I _y, следовательно, сечение потерявшего устойчивость стержня будут поворачиваться вокруг оси X, при этом определяющим при расчете гибкости стойки окажется

окончательно получим

i_{x (min)}= 0,9129 a.

 

Рис. 6

2. Определим гибкость первого приближения

λ _max = μ l / i _min = 3,0671 / a.

3. При первоначальном назначении размера a следует руководствоваться опытом или интуицией. Из соображений здравого смысла зададимся величиной a = 0,005 м. Тогда значение гибкости первого приближения будет равно λ = 61,343. Воспользуемся табл.9 заданий на контрольные работы и выберем в качестве материала стойки Сталь 5. Будем иметь следующие исходные значения для проведения линейной интерполяции:

при λ = 60 φ = 0,80

при λ = 70 φ = 0,74.

С учетом этих данных для λ = 61,343 получим:

4. Определенное нами значение φ подставим в выражение (22) и выясним, удовлетворяется ли неравенство. Имеем:

что подтверждает наличие устойчивого деформирования и отсутствие потери устойчивости при заданных размерах. Однако существенная недогрузка стойки в данном случае является очевидной, т.к.

и составляет 73,2 %, что, конечно же, является экономически неоправданным и с точки зрения проектировщика недопустимым. В связи с этим сделаем второе приближение, уменьшив характерный размер a.

5. Зададим a = 0,0035 м. Тогда значение гибкости второго приближения будет равно λ = 87,631. Вновь воспользуемся табл. 9 заданий на контрольные работы и выберем исходные значения для проведения линейной интерполяции:

при λ = 80 φ = 0,67

при λ = 90 φ = 0,59.

С учетом этих данных для λ = 87,631 получим:

6. Определенное нами значение φ второго приближения подставим в выражение (22) и выясним, удовлетворяется ли теперь неравенство. Имеем:

что подтверждает наличие устойчивого деформирования и отсутствие потери устойчивости и при уточненных размерах. Однако недонапряжение стойки в данном случае также является чрезмерным, поскольку