Сталь прокатная. Балка двутавровая. ГОСТ 8239-56

 

 

Номер профиля	Размеры, мм	Площадь сечения, см2	Справочные величины для осей х-х
h	b	d	t
Ix, см4	Wx, см3	Sx, см3
			4,5	7,2	12,0		39,7	23,0
			4,8	7,3	14,7		58,4	33,7
			4,9	7,5	17,4		81,7	46,8
			5,0	7,8	20,2			62,3
			5,1	8,1	23,4			81,4
18а			5,1	8,3	25,4			89,8
			5,2	8,4	26,8
20а			5,2	8,6	28,9
			5,4	8,7	30,6
22а			5,4	8,9	32,8
			5,6	9,5	34,8
24а			5,6	9,8	37,5
			6,0	9,8	40,2
27а			6,0	10,2	43,2
			6,5	10,2	46,5
30а			6,5	10,7	49,9
			7,0	11,2	53,8
			7,5	12,3	61,9
			8,0	13,0	71,4
			8,6	14,2	83,0
			9,5	15,2	97,8
			10,3	16,5	114,0
			11,1	17,8	132,0
			12,0	19,2	153,0
			13,0	20,8	176,0
70а			15,0	24,0	202,0
70б			17,5	28,2	234,0

 

СЛОЖНОЕ СОПРОТИВЛЕНИЕ

 

Задачи № 6 и 7 относятся к разделу Сложного сопротивления.

Сложным сопротивлением называется такое нагружение стержня, когда в его поперечном сечении возникают несколько внутренних силовых факторов, существенно влияющих на напряженное состояние.

В зависимости от наличия тех или иных внутренних факторов сложное сопротивление бывает нескольких видов.

 

1. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ ИЛИ СЖАТИЕ

В задаче № 6 рассматривается случай внецентренного растяжения – сжатия стержней. Этот вид нагружения довольно распространен в технике, так как в реальной ситуации почти невозможно приложить растягивающую нагрузку точно в центре тяжести.

Внецентренным растяжением-сжатием называется случай, когда равнодействующая сил, приложенных к отброшенной части стержня, направлена параллельно оси стержня, но не совпадает с этой осью (рис.1).

Рис.1

Представим, что после проведения разреза равнодействующая Р сил действующих на отброшенную часть и приложенная к оставшейся проходит через точку с координатами в главных центральных осях поперечного сечения (рис. 2).

Рис.2

Приведем силу Р в центр тяжести сечения, т.е. направим вдоль оси стержня (сила N). При этом появятся две пары сил относительно главных центральных осей (рис.3).

Таким образом, в поперечном сечении стержня при внецентренном растяжении и сжатии возникают три внутренних силовых фактора: нормальная сила N и два изгибающих момента относительно главных центральных осей поперечного сечения.

Для вычисления нормального напряжения в поперечном сечении в окрестности точки с произвольными координатами 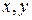воспользуемся принципом независимости действия сил. Будем вычислять нормальное напряжение от каждого внутреннего силового фактора в отдельности и результат сложим.

 

Рис.3.

 

(1.1)

По этой формуле можно вычислять нормальные напряжения в точках поперечного сечения стержня при совместном действии осевой силы и двух изгибающих моментов. В нашем случае все три внутренних силовых фактора зависят от внецентренно приложенной силы Р (рис.3). Подставив соответствующие выражения в (1.1), получим (1.2)

Вынесем величину нормального напряжения при осевом растяжении за скобки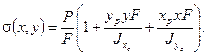

Введем понятие о радиусе инерции относительно оси U 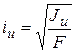- (1.3)

это такое расстояние от оси U до условной точки, где сосредоточена вся площадь сечения. Тогда момент инерции можно найти по формуле

(1.4)

Применив (1.4) в выражении , получим

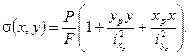(1.5)

Мы получили формулу нормальных напряжений в поперечном сечении при внецентренном растяжении или сжатии. Если сила растягивающая, то перед скобкой ставится знак плюс, если сила сжимающая, то ставится – минус.

В этой формуле координаты точки, где определяются напряжения входят в первой степени. Следовательно, если величины напряжений откладывать в масштабе в виде аппликат перпендикулярно плоскости поперечного сечения, то концы этих отрезков будут лежать на плоскости, наклоненной к плоскости поперечного сечения. Будем называть эту плоскость плоскостью напряжений. Известно, что две наклоненные плоскости пересекаются по линии. В нашем случае в точках этой линии - это нулевая линия, которая описывается уравнением (1.6)

Анализируя (1.6) можно сделать вывод, что нейтральная линия при внецентренном растяжении и сжатии не проходит через центр тяжести, а отсекает на главных центральных осях отрезки 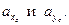Полагая последовательно в (1.6) , получим (1.7)

Учитывая, что числители в формулах (1.7) всегда положительны, можно сделать вывод о том, что положение отрезков на плоскости поперечного сечения связано с положением внецентренной силы: нулевая линия всегда проходит в квадрате, противоположном квадрату, где находится точка приложения силы (рис.4).

 

Для сечений со сложным контуром знание положения нулевой линии очень важно. Вспоминая про понятие плоскость напряжений, можно утверждать, что наибольшие по величине нормальные напряжения возникают в точках поперечного сечения наиболее удаленных от нулевой линии. Если взглянуть на плоскость напряжений вдоль нулевой линии, то она будет видна в виде линии соединяющей аппликаты напряжений, то есть в виде эпюры напряжений, отложенной от линии перпендикулярной нулевой линии (рис.4).

Наибольшее растягивающее нормальное напряжение возникает в точке А

(1.8)

а наибольшее сжимающее нормальное напряжение возникает в точке В

(1.9)

Таким образом, при внецентренном растяжении кроме растягивающих нормальных напряжений в поперечном сечении могут возникнуть и сжимающие. При внецентренном сжатии – наоборот.

В некоторых случаях в технике появление в поперечном сечении нормальных напряжений разных знаков нежелательно. Добиться появления в поперечном сечении нормальных напряжений одного знака можно, используя понятие ядра сечения.

Ядро сечения

Ядром сечения называется область поперечного сечения, включающая центр тяжести, точки которой обладают следующим свойством: если внецентренная сила приложена в пределах ядра сечения, то нормальные напряжения во всех точках поперечного сечения будут одного знака.

При приложении силы Р в точке на границе ядра сечения с координатами нулевая линия будет касательной к контуру поперечного сечения в точке В (рис.5) и отсекать на главных центральных осях отрезки .

рис. 5

 

Применяя (1.7), получим (1.10)

Формулы (1.10) описывают алгоритм вычисления координат точек границы ядра сечения:

1. Проводится касательная к контуру поперечного сечения и определяются отрезки .

2. По формуле (1.10) определяются координаты

Такая процедура проводится со всеми касательными. Для сложного криволинейного контура, чем больше будет проведено касательных, тем точнее будет найден контур ядра сечения.

Можно доказать, что если касательная будет вращаться вокруг угла контура сечения, если он есть, то соответствующая точка на контуре ядра будет перемещаться по прямой линии, соединяющей точки ядра соответствующие крайним положениям касательных.

Таким образом, если контур поперечного сечения представляет собой многоугольник, что контур ядра сечения тоже будет иметь форму многоугольника, но необязательно с тем же количеством углов (их может быть меньше).

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: