 |
Схема II. Балка на двух опорах
|
|
|
|
1. Для определения опорных реакций воспользуемся уравнениями статики. В общем случае для плоской системы нагрузок таких уравнений будет три:
Σ mA = 0, Σ mB = 0, Σ z = 0.
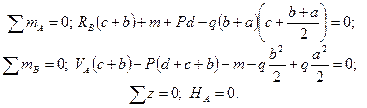
Записывая, а затем, решая их, получим
V A = 65 кН, R B = 105 кН.
Горизонтальная составляющая реакции в опоре А равна нулю, поскольку все внешние нагрузки действуют вдоль вертикали. Направление реакций V A и R B указано на рис. 30а.[1]
2. Как и ранее предполагается, что на всем своем протяжении балка имеет одинаковую изгибную жесткость EJx, что выражается в неизменности геометрических размеров сечения по длине балки, а также в постоянстве механических свойств (вся балка изготовлена из одного материала). При этих ограничениях для возникновения каждого нового участка достаточно изменения характера внешней нагрузки (в нашем случае это появление сосредоточенной силы, момента, начало или окончание действия равномерно распределенной нагрузки). Рассуждая, таким образом, устанавливаем, что число участков для нашей расчетной схемы будет равно четырем (рис. 30а).
3. Проводя последовательно сечения на первом и втором участках, будем рассматривать равновесие правой отсеченной части. При движении слева направо (участки 3 и 4) будем рассматривать равновесие левой отсеченной части (рис. 31).
Обход балки с разных сторон целесообразен в тех случаях, когда число участков превышает два. В случае же, если мы будем осуществлять расчет, двигаясь в одном направлении, количество слагаемых от участка к участку будет существенно возрастать, что неизбежно приведет к увеличению объема вычислений.
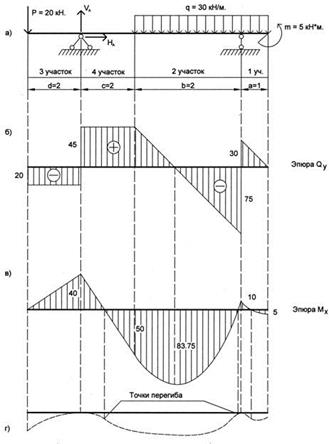
рис. 30
Имеем:
Для первого участка (0≤ z 1 ≤ a):
 Qy = + q z 1(наклонная линия)
Qy = + q z 1(наклонная линия)
 Mx = + m - q
Mx = + m - q  /2 (квадратная парабола)
/2 (квадратная парабола)
|
|
|
Для второго участка (0≤ z 2 ≤ b):
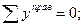 Qy = - RB + q (a + z 2 ) (наклонная линия)
Qy = - RB + q (a + z 2 ) (наклонная линия)
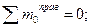 Mx = + m - q (a + z 2 ) 2 /2 + RB z 2(квадратная парабола)
Mx = + m - q (a + z 2 ) 2 /2 + RB z 2(квадратная парабола)
Для третьего участка (0≤ z 3 ≤ d):
 Qy = - P (константа)
Qy = - P (константа)
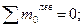 Mx = - P z (наклонная линия)
Mx = - P z (наклонная линия)
Для четвертого участка (0≤ z 4 ≤ с):
 Qy = - P + VA (константа)
Qy = - P + VA (константа)
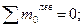 Mx = - P (d + z 4 ) + VA z 4(наклонная линия)
Mx = - P (d + z 4 ) + VA z 4(наклонная линия)
4. Определим теперь числовые значения Qy и Mx в характерных сечениях (как и в случае консольной балки, сначала рассмотрим лишь точки, соответствующие началу и концу каждого из участков).
Первый участок:
При z = 0 Qy = 0 Mx = m
При z = a Qy = q a Mx = m - q a 2 /2
Второй участок:
При z = 0 Qy = q a - RB Mx = m - q a 2 /2
При z = b Qy = q (a+b) - RB Mx = m - q (a+b) 2 /2 + RB b
Третий участок:
При z = 0 Qy = - P Mx = 0
При z = d Qy = - P Mx = - P d
Четвертый участок:
При z = 0 Qy = - P + RA Mx = - P d
При z = c Qy = - P + RA Mx = - P (c+d) + RA c
Для наглядности вычислим значения ординат при следующих числовых значениях:
a = 1 м, b = 4 м, c = 2 м, d = 2 м, P = 20 кН, m = 5 кНм, q = 30 кН/м и сведем полученные результаты в таблицу 3.2:
Таблица 3.2
| № участка | z, м | Qy, кН | Mx, кНм |
| 1 участок | z = 0 z = 1 | Qy = 0 Qy = 30 | Mx = 5 Mx = -10 |
| 2 участок | z = 0 z = 4 | Qy = -75 Qy = 45 | Mx = 20 Mx = 50 |
| 3 участок | z = 0 z = 2 | Qy = -20 Qy = -20 | Mx = 0 Mx = -40 |
| 4 участок | z = 0 z = 2 | Qy = 45 Qy = 45 | Mx = -40 Mx = 50 |
Анализируя закон изменения Qy на втором участке, видим, что эпюра меняет знак. Точка перехода Qy через ноль даст нам координату экстремума z * (см рис.30б) на эпюре изгибающих моментов (рис.30в). Определим эту точку:
Qy = - RB + q (a + z) = 0, откуда z * = (RB – q a) / q = 2,5 м.
Подставляя полученное значение z * в уравнение момента на втором участке, получим величину экстремума, который даст третью (промежуточную) точку для построения эпюры Mx:
Mx = + m - q (a + z * ) 2 /2 + RB z * = 83,75 кНм.
5. По полученным данным (табл.3.2) в той же последовательности, что и для консольной балки, строим эпюры поперечных сил и изгибающих моментов (рис.30б и 30в).
6. Проведем теперь проверку правильности построения эпюр. Прежде всего, установим соответствие между эпюрами изгибающих моментов и поперечных сил на каждом из участков. Ранее было показано, что порядок линии, описывающей Qy на единицу меньше, чем порядок линии, описывающей Mx. У нас на первом и втором участках эпюра Mx представляет собой параболу, а эпюра Qy - наклонную прямую, на третьем и четвертом участках соответственно Mx - наклонная прямая, Qy - константа. Очевидно, что дифференциальная зависимость dMx /dz = Qy на всех участках выполняется. Кроме того, отмечаем, что при Qy = 0 эпюра моментов имеет максимальное значение (экстремум), что также говорит об удовлетворении указанной дифференциальной зависимости.
|
|
|
Помня о том, что внешние сосредоточенные силовые факторы должны давать на соответствующих им эпюрах скачки, убеждаемся, что под P, VA, RB и m действительно есть такие изменения ординат (на 20 кН, 65 кН и 105 кН в эпюре Qy и 5 кНм - в эпюре Mx). Таким образом, делаем вывод, что эпюры построены правильно.
7. При вычерчивании изображения примерного вида изогнутой оси балки помимо рассуждений о соответствии её кривизны расположению эпюры моментов (подробности изложены ранее при расчете консольной схемы), отметим также, что в отличие от первого случая здесь имеются две характерные точки (опоры А и В), в которых перемещения равны нулю. Построение обычно начинают с участков, прилегающих к точкам опор (или включающих в себя эти точки). По эпюре моментов делаем вывод, что упругая линия имеет три точки перегиба, комбинируя виды балки изображенные на рис. 28а и 28б, сопрягая участки упругой линии в точках перегиба и не забывая при этом, что на опорах перемещения отсутствуют, строим окончательную кривую, представленную на рис. 30г.
8. Поскольку балка в нашем примере должна быть изготовлена из двутавра, очевидно, что ее поперечное сечение, а также механические свойства по длине остаются неизменными, следовательно, расчет на прочность следует проводить для сечения, в котором действует максимальный изгибающий момент Mx = 83,75 кНм (опасное сечение).
9. Номер двутавра для балки подбираем из условия прочности при изгибе и допускаемом напряжении 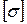 = 200 МПа (сталь):
= 200 МПа (сталь):
σ = Mmax / Wx ≤  ,
,
откуда требуемый момент сопротивления должен быть больше или равен
Wxтр = 418,75 см3.
10. По сортаменту (ГОСТ 8239-72 Приложение 1) выбираем двутавр № 30 с Wx = 472 см3.
|
|
|
рис. 31
ЗАДАЧА № 4
Задача относится к разделу «Определение перемещений при изгибе балок». В задании требуется найти компоненты перемещений балки, рассчитанной в задаче № 3.
Мы рассмотрим новую схему (рис.32).
Приведем эпюры М и Q для балки по схеме № 4 Задачи № 3: при а =2 м; q =10 кН/м; С =1,5 а; М =0,5 qa 2; Р =0,8 qa; М 0= М;  =200 МПа (рис.32).
=200 МПа (рис.32).
Из условия прочности выбрано сечение балки в виде двутавра № 33 Wx =597 см3=5,97×10-4 м3; Jх =9,84×10-6 м4; Е =2,1×108 кН/м2; EJх =2,066×104 кНм2.
Наибольшее напряжение в сечении М max=113,3 кНм составляет 
Недонапряжение составляет 5%, что допустимо.
На этом результате должна заканчиваться задача №3. Далее определяем перемещения в точках 1 и 2 балки (рис.32а). Состояние балки под действием заданной нагрузки обозначим q.
Определим вертикальное перемещение  центра сечения, где приложен сосредоточенный момент. Для этого рассмотрим балку в состоянии
центра сечения, где приложен сосредоточенный момент. Для этого рассмотрим балку в состоянии  под действием только сосредоточенной силы
под действием только сосредоточенной силы  приложенной в точке 1 перпендикулярно оси балки (по направлению искомого перемещения
приложенной в точке 1 перпендикулярно оси балки (по направлению искомого перемещения  ) (рис.32г).
) (рис.32г).
Вычислим опорные реакции, составив три уравнения равновесия

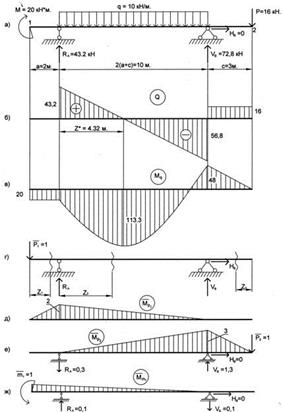
рис. 32
Проверка 
Реакции найдены верно.
Для построения эпюры  рассмотрим три участка (рис.32г).
рассмотрим три участка (рис.32г).
1 участок

2 участок
3 участок

По этим данным строим эпюру  (рис.32д) со стороны растянутых волокон.
(рис.32д) со стороны растянутых волокон.
Определим  по формуле Мора (58) с помощью правила Верещагина. При этом криволинейную эпюру
по формуле Мора (58) с помощью правила Верещагина. При этом криволинейную эпюру 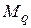 , на участке между опорами, можно представить в виде сложения трех эпюр, как показано на рис. 23. Стрелка
, на участке между опорами, можно представить в виде сложения трех эпюр, как показано на рис. 23. Стрелка
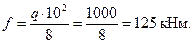

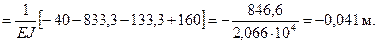
Знак «минус» означает, что точка 1 перемещается вверх (в направлении противоположном  ).
).
Определим вертикальное перемещение 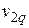 точки 2, где приложена сосредоточенная сила. Для этого рассмотрим балку в состоянии
точки 2, где приложена сосредоточенная сила. Для этого рассмотрим балку в состоянии  под действием только сосредоточенной силы
под действием только сосредоточенной силы 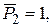 приложенной в точке 2 перпендикулярно оси балки (по направлению искомого перемещения
приложенной в точке 2 перпендикулярно оси балки (по направлению искомого перемещения 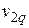 ) (рис.32е).
) (рис.32е).
Эпюра  строится аналогично предыдущей.
строится аналогично предыдущей.
Далее по формуле Мора (58)
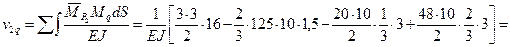
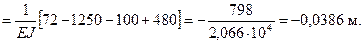
Точка 2 перемещается вверх.
Определим угол поворота 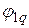 сечения, где приложен сосредоточенный момент.
сечения, где приложен сосредоточенный момент.
|
|
|
Для этого рассмотрим балку в состоянии  под действием только сосредоточенного момента
под действием только сосредоточенного момента 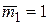 , приложенного в сечении 1 против часовой стрелки (рис.32ж).
, приложенного в сечении 1 против часовой стрелки (рис.32ж).
Вычислим опорные реакции, составив три уравнения равновесия.
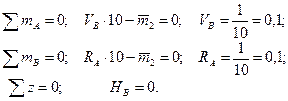
Проверка  Реакции найдены верно
Реакции найдены верно
Эпюра  показана на рис.32ж.
показана на рис.32ж.
Далее по формуле Мора (59)

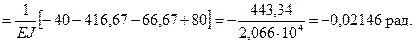
Сечение 1 поворачивается по часовой стрелке.
ЗАДАЧА № 5
Исходные данные те же, что в задаче № 4, но в точке на оси, где приложен сосредоточенный момент, устанавливаем шарнирно подвижную опору (рис.33а). Балка становится один раз статически неопределимой. Для вновь созданной балки необходимо:
1. Построить эпюры М и Q.
2. Определить по формуле Мора вертикальное перемещение центра сечения, где приложена сосредоточенная сила.
3. Вычертить приблизительный вид изогнутой оси балки.
4. Определить новые размеры двутаврового поперечного сечения из условия прочности при 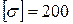 МПа (сталь) и величину прогиба точки в п.2.
МПа (сталь) и величину прогиба точки в п.2.
5. Сравнить статически определимую и статически неопределимую балки.

рис. 33
Пример решения
1. Алгоритм расчета один раз статически неопределимых балок приведен в формулах (59)-(61). Выбираем основную систему. Для этого отбросим вновь поставленную связь и заменим ее действие неизвестной реакцией Х1 (рис.33б). Полученная основная система является статически определимой (она рассчитана в задачах № 3,4) и находится под действием заданной нагрузки и неизвестной силы Х1.
Можно было бы отбросить какую-либо другую связь и заменить ее действие неизвестным силовым фактором Х1. При этом полученная система должна быть геометрически неизменяемой, то есть не имеющей возможности получать перемещения без возникновения напряжений.
Мы выбираем основную систему в виде балки на рис.33б, потому, что у нас уже построены для нее необходимые эпюры в задаче № 4.
Для основной системы запишем уравнение деформации типа (59):
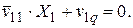 (62)
(62)
Для определения  по формуле (60) рассмотрим основную систему под действием силы
по формуле (60) рассмотрим основную систему под действием силы 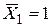 (рис.33в). Эпюра
(рис.33в). Эпюра  (рис.33г) будет та же, что при действии силы
(рис.33г) будет та же, что при действии силы  вниз в задаче №4, но с обратным знаком.
вниз в задаче №4, но с обратным знаком.
Применим формулу Мора (60). Нужно с помощью правила Верещагина «перемножить» эпюру  «саму на себя»:
«саму на себя»:
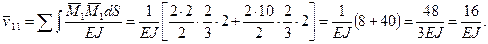
Величину  мы определили при решении задачи №4
мы определили при решении задачи №4 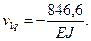
Минус означает, что прогиб направлен в противоположную сторону, чем  . В нашем случае все определяет направление
. В нашем случае все определяет направление 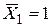 :
:  совпадает с направлением
совпадает с направлением 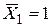 (вверх), поэтому в уравнение деформации поставим
(вверх), поэтому в уравнение деформации поставим  с положительным знаком
с положительным знаком 
Итак уравнение для Х1 будет иметь вид 
Отсюда 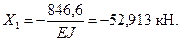
Интересно, что жесткость сечения на изгиб сокращается. Величина Х1 от заданной нагрузки будет одинаковой для балок с любым поперечным сечением постоянным по длине.
|
|
|
Знак минус означает, что на самом деле реакция Х1 направлена вниз.
Теперь на основную систему действуют известная внешняя нагрузка и известная сила Х1. Эпюры Qy и Mx, вычисленные для основной системы будут соответствовать тем же эпюрам в заданной статически неопределимой балке.
Вычислим опорные реакции. Для этого запишем три уравнения статического равновесия:

Проверка: 

Реакции найдены верно.
Балку разбиваем на 3 участка. На каждом участке разрезаем балку на две части, и рассматриваем равновесие оставшейся части (подобно рис. 31) длина которой является переменной 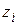 , получаем аналитические выражения для ординат эпюр Qy и Mx.
, получаем аналитические выражения для ординат эпюр Qy и Mx.
1 участок
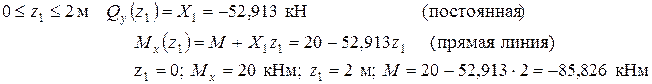 2 участок
2 участок
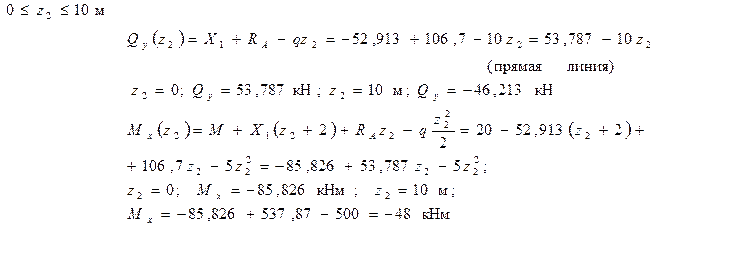 Определяем экстремальное значение
Определяем экстремальное значение
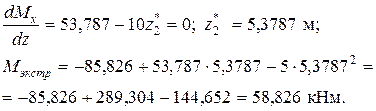
3 участок

Эпюра Qy показана на рис. 33д, а эпюра Mx – на рис.33е.
2. Определяем прогиб  точки, где приложена сосредоточенная сила по формуле (55)
точки, где приложена сосредоточенная сила по формуле (55) 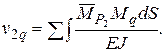
Эпюра  (рис.32) построена в процессе решения задачи №4. Сила
(рис.32) построена в процессе решения задачи №4. Сила  =1 приложена не к заданной статически неопределимой балке, а к основной системе. Дело в том, если к основной системе приложить все внешние силы и известную силу
=1 приложена не к заданной статически неопределимой балке, а к основной системе. Дело в том, если к основной системе приложить все внешние силы и известную силу  , то она будет полностью эквивалента заданной статически неопределимой балке.
, то она будет полностью эквивалента заданной статически неопределимой балке.
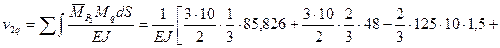


Точка 2 перемещается верх, но на гораздо меньшую величину, чем в случае статически определимой балки.
В определимой балке 
В неопределимой балке 
Прогиб уменьшился в 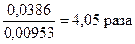 .
.
3. Приблизительный вид изогнутой оси балки строим в соответствии с видом эпюры  и характером опор (рис. 33ж).
и характером опор (рис. 33ж).
4. Максимальное значение изгибающего момента возникает над опорой А
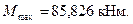
Из условия прочности 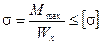
определяем двутавровое сечение для статически неопределимой балки

По сортаменту (приложение 1) выбираем двутавр № 30 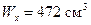
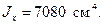
Вычисляем напряжения в опасном сечении

Недонапряжение составляет 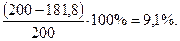
Шаг сортамента не позволяет выбрать более экономное решение. Определяем величину прогиба точки 2 балки с новым сечением. Жесткость сечения при изгибе 
5. Таким образом, постановка шарнирно подвижной опоры в точке 1 превращает статически определимую балку в статически неопределимую.
При этом сечение балки из условия прочности можно принять меньшим (вместо I № 33 можно принять I № 30).
Подсчитаем экономию по массе металла:
масса 1 погонного метра I №33 – 42,2 кг;
масса 1 погонного метра I № 30 – 36,5 кг.
Экономия 
Прогиб точки приложения сосредоточенной силы уменьшается в 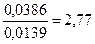 раза.
раза.
Приложение 1
|
|
|


