 |
Формирование системы операторов j
|
|
|
|
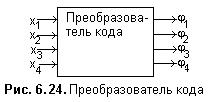
Пусть необходимо разработать преобразователь четырехразрядного двоичного кода в код Штибитца (см. рис.6.24).
| Таблица 6.44 | По данным таблицы 6.44 составлены четыре карты Карно (рис. 6.25). Сравнивая соответствующие клетки четырех карт, можно выделить одинаковую смежность на двух, трех и/или четырех картах, что позволит унифицировать и минимизировать описание булевых функций. Выбор минимальной булевой функции нужно проверить на ДНФ и КНФ. Ниже приведены минимальные булевы функции ДНФ и КНФ. Скобками в формулах выделены одинаковые | |||||||||||||||||||
| xi | ji | |||||||||||||||||||
| x1 | x2 | x3 | x4 | j1 | j2 | j3 | j4 | |||||||||||||
| j1 |  x1 x1 
| j2 |   x1 x1
| |||||||||||||||||
| x2 | x2 | |||||||||||||||||||
| x4 | x4 | |||||||||||||||||||
  x3 x3
|   x3 x3
| |||||||||||||||||||
 j3 j3
|  x1 x1
|  j4 j4
|  x1 x1
| |||||||||||||||||
| x2 | x2 | |||||||||||||||||||
| x4 | ||||||||||||||||||||
  x3 x3
|   x3 x3
| |||||||||||||||||||
| Рис. 6.25Карты Карно четырехразрядного преобразователя кода. | ||||||||||||||||||||
|
|
|
 j1=1=`x1,
j1=1=`x1,
 j2=1=(`x1×`x2)Úx1×x2=x1«x2=(x1Åx2),
j2=1=(`x1×`x2)Úx1×x2=x1«x2=(x1Åx2),
j3=1=(`x1×`x2)×x3Ú x2×`x3 Úx1×`x3,
j4=1=(`x1×`x2)×x4Ú`x3×x4 Ú(x1Úx2)×(x3×`x4).
 j1=0=`x1,
j1=0=`x1,
j2=0=(`x1Úx2)×(x1Ú`x2)=x1«x2=(x1Åx2),
j3=0=(`x2Ú`x3)×(`x1Ú`x3)×((x1Úx2)Úx3),
j4=0=(x3Úx4)×((`x1Ú`x3)Ú`x4)×((`x2Ú`x3)Ú`x4)×((x1Úx2)Úx4).
Система булевых функций используется при создании дешифраторов или преобразователей кодов, при формировании нескольких команд на исполнение одного задания и т.п.
Логическая схема комбинационного автомата

Комбинационные автоматы реализуют логические функции с помощью логических схем. Для проектирования комбинационных автоматов разработаны стандарты обозначения различных логических схем.
На рис. 6.26. приведены основные логические схемы для элементарных булевых функций двух булевых переменных. Реальная аппаратура содержит в одной микросхеме большое число элементарных логических схем, что существенно упрощает формирование логической сети. Микросхемы (такова особенность микроэлектроники) реализуют большинство логических функций в базисе "И-НЕ" и "ИЛИ-НЕ. В этом случае инверсия булевой переменной может быть реализована также на логической схеме "И-НЕ" или "ИЛИ-НЕ, объединив два входных канала.
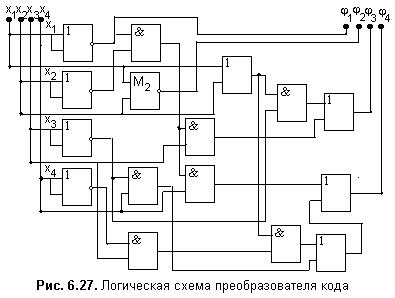
На рис. 6.27 представлена логическая схема комбинационного автомата преобразователя двоичного кода в код Штибитца, спроектированная по минимальным булевым функциям для fi=1.
|
|
|
6.3.3. Автоматы с “памятью”
В качестве элементов “памяти” (или двоичной задержки на один такт) чаще всего используют триггеры.
Триггер – это элементарный автомат Мура, обладающий двумя устойчивыми состояниями 0 и 1. Существует несколько разновидностей триггеров. Их различия обусловлены способами формирования входных и выходных сигналов. Схемы и таблицы переходов каждого типа триггеров представлены на рис. 6.28. Входы D, T, RS и JK - триггеров называют информационными. D- и T-триггеры обладают одним информационным входом, а RS- и JK-триггеры – двумя.
. Выходы триггеров формируют задержку (или запоминание) сигнала до следующего его приема на информационном входе.
Для этого необходимо создать функцию возбуждения триггера в соответствии с функцией переходов автомата:
q[t+1]=y(q1[t]; q2[t];…qm[t]; x1[t];x2[t];…xn[t]).
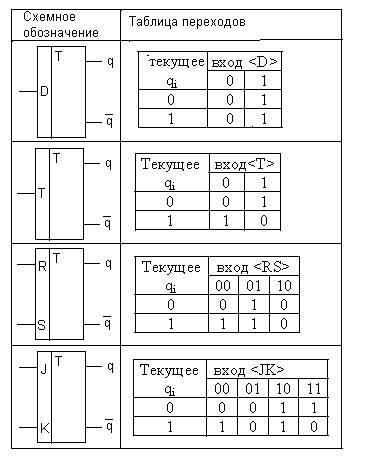
Рис. 6.28. Схемы и таблицы переходов триггеров.
В реальной аппаратуре существуют вспомогательные каналы триггера для синхронизации и принудительной установки триггера в состояния 0 или 1. В настоящем пособии эти каналы не рассматриваются. Выбор конкретного типа триггера определяется конструкторско-технологическими задачами проектирования дискретного устройства.
Формирование оператора j
Особенность формирования оператора j состоит в учете влияния каждой компоненты булевых векторов q и x, т. е.
yi=j(q1, q2, … qm, x1, x2,…xn). Поэтому при описании каждого значения функции выхода yi в таблице выходов следует учитывать значения каждой компоненты булевых векторов
Пусть дана таблица выхода минимизированного автомата в кодах входных сигналов и внутренних состояний.
| q3q2q1) | (x2x1) | ||
На рис. 6.30 приведена карта на пять двоичных переменных и выполнена минимизация ДНФ и КНФ по методу, изложенному в 6.3.2.
  x1 x1
| 
|  x1 x1
| |||||||
  q3 q3
| |||||||||
| q2 | * | * | * | * | * | * | |||
| * | * | * | * | x2 | |||||
| * | * | ||||||||
| * | * | * | * | * | |||||

|  q1 q1
| ||||||||
| Рис. 6.30. Карта Карно функции выхода |
Тогда СДНФ и СКНФ функции выхода имеют формулу:
|
|
|
y=1=`q3×`q2×q1×`x2×x1 Ú `q3×q2×q1×`x2×x1 Ú`q3×q2×`q1×x2×`x1 Úq3×`q2×`q1×x2×`x1 Úq3×`q2×q1×x2×`x1 Ú `q3×q2×`q1×x2×x1 Ú q3×`q2×`q1×x2×x1 Úq3×`q2×q1×x2×x1,
y=0=(q3Ú`q2Úq1Úx2Ú`x1)×(`q3Úq2Úq1Úx2Ú`x1)×(`q3Úq2Ú`q1Úx2Ú`x1)×
(q3Úq2Ú`q1Ú`x2Úx1)×(q3Ú`q2Ú`q1Ú`x2Úx1)×(q3Úq2Ú`q1Ú`x2Ú`x1)×
(q3Ú`q2Ú`q1Ú`x2Ú`x1).
Анализ карты Карно позволяет составить минимальную ДНФ и КНФ, воспользовавшись неопределенными значениями в клетках, помеченных знаком “*”.
jmin(q1, q2, q3, x1, x2)=1=q3×x2Ú`q1×x2Ú`q3×q1×`x2,
jmin(q1, q2, q3, x1, x2)=0=(`q3Úx2)×(q3Ú`q1Ú`x2)×(q1Úx2).
Формирование оператора y
По кодированной таблице переходов автомата можно определить для каждого разряда вектора q[t+1]=(q1[t+1], q2[t+1],...qm[t+1]) зависимость с каждым разрядом векторов q[t]=(q1[t], q2[t],...qm[t]) и x[t]=(x1[t], x2[t],...xn[t]).
Пусть дана таблица переходов минимизированного автомата, представленная в кодах входных сигналов и внутренних состояний.
| (q3q2q1) | (x2x1) | ||
По этой таблице для каждого типа триггера (см. рис. 6.27) можно сформировать сигналы в каждом разряде для перевода его из состояния qi[t] в состояние. qi[t+1], т. е. построить таблицу возбуждения триггера.
Пусть дан JK-триггер, имеющий два информационных входа. В каждой клетке таблицы 6.45 верхняя строка есть информационный вход J, а нижняя строка – информационный вход K.. В каждой клетке таблицы символом “*” отмечены позиции (qi, J) и (qi, K), в которых допустимы любые значения информационного сигнала.
По сформированной таблице 6.45 перейти к формированию оператора y (см. рис. 6.19) или функции возбуждения памяти автомата в форме СДНФ или СКНФ.
| Таблица 6.45. | ||||
| (q3q2q1) | (x2x1) | |||
| 0 1 0 * * * | 0 1 0 * * * | 0 1 * * * 0 | J K | |
| 0 * 1 * 1 * | 0 * 0 * 0 * | 0 1 * * * 0 | J K | |
| 1 * * * 1 1 | 0 * * * 0 1 | 0 * * * 1 0 | J K | |
| * 0 0 1* * | * 0 1 0 * * | * 0 0 0 * * | J K | |
| * 1 * 1 * 0 | * 0 * 0 * 0 | * 1 * 1 * 0 | J K | |
| q3q2q1 | q3q2q1 | q3q2q1 |
|
|
|
 Например, система функций возбуждения памяти автомата в форме СДНФ, составленная по таблице 6.45 имеет вид:
Например, система функций возбуждения памяти автомата в форме СДНФ, составленная по таблице 6.45 имеет вид:
U(J3)=`q3×q2×q1×`x2×x1
U(K3)=q3×`q2×`q1×`x2×x1Úq3×`q2×q1×`x2×x1Úq3×`q2×q1×x2×x1
 U(J2)=`q3×`q2×q1×`x2×x1Úq3×`q2×q1×`x2×x1Ú`q3×`q2×q1×x2×`x1Ú
U(J2)=`q3×`q2×q1×`x2×x1Úq3×`q2×q1×`x2×x1Ú`q3×`q2×q1×x2×`x1Ú
Ú`q3×`q2×q1×x2×x1 Ú`q3×q2×`q1×x2×x1Úq3×`q2×q1×x2×x1
U(K2)=`q3×q2×`q1×`x2×x1Ú`q3×q2×q1×`x2×x1Ú`q3×q2×q1×x2×x1
 U(J1)=`q3×q2×`q1×`x2×x1Úq3×`q2×`q1×x2×`x1
U(J1)=`q3×q2×`q1×`x2×x1Úq3×`q2×`q1×x2×`x1
U(K1)=`q3×q2×q1×`x2×x1Ú`q3×q2×q1×x2×`x1
Минимизировать состав и структуру системы функций возбуждения удобнее выполнять на картах Карно по методу, изложенному в 6.3.2.2. Каждой карте Карно присвоено имя U(Ji) или U(Ki), где U – сигнал возбуждения триггера, J – информационный вход JK-триггера, K – информационный вход JK-триггера, i –разряд регистра внутренних состояний автомата (iÎ{1, 2, 3}
Для этого по таблице 6.45 составим карты Карно по каждому информационному входу (J и K) каждого разряда кода внутреннего состояния автомата (q1, q2, q3).
Анализ карт Карно позволяет найти минимальные функции возбуждения по каждому информационному входу и каждому разряду регистра внутренних состояний с учетом безразличного значения в некоторых клетках таблицы, отмеченного знаком “*”.
| U(J3) | x1 | x1 | U(K3) | x1 | x1 | |||||||||||||||
  q3 q3
| 
|  q3 q3
| ||||||||||||||||||
| q2 | * | * | * | * | * | * | q2 | * | * | * | * | * | * | * | * | |||||
| * | * | * | * | x2 | * | * | * | * | * | * | * | * | x2 | |||||||
| * | * | * | * | * | * | * | * | * | * | * | ||||||||||
| * | * | * | * | * | * | * | * | * | * | * | * | |||||||||
  q1 q1
|   q1 q1
|
| U(J2) | x1 | x1 | U(K2) | x1 | x1 | |||||||||||||||

|  q3 q3
|   q3 q3
| ||||||||||||||||||
| q2 | * | * | * | * | * | * | * | * | q2 | * | * | * | * | * | * | |||||
| * | * | * | * | * | * | * | x2 | * | * | * | * | * | x2 | |||||||
| * | * | * | * | * | * | * | * | * | * | |||||||||||
| * | * | * | * | * | * | * | * | * | * | * | * | * | ||||||||
  q1 q1
|   q1 q1
| |||||||||||||||||||
| U(J1) | x1 | x1 | U(K1) | x1 | x1 | |||||||||||||||
  q3 q3
|   q3 q3
| |||||||||||||||||||
| q2 | * | * | * | * | * | * | * | q2 | * | * | * | * | * | * | * | |||||
| * | * | * | * | * | * | * | x2 | * | * | * | * | * | * | x2 | ||||||
| * | * | * | * | * | * | * | * | * | * | |||||||||||
| * | * | * | * | * | * | * | * | * | * | * | * | * | ||||||||
  q1 q1
|   q1 q1
|
|
|
|
Ниже представлены минимальные ДНФ для каждой функции.
 U(J3)=q2q1×`x2,
U(J3)=q2q1×`x2,
U(K3)=`x2Úq1×x1,
U(J2)=`q3Úq1×x1,
U(K2)=x1,
U(J1)=q3×`x1Úq2×`x2,
U(K1)=q2×`x1Úq2×`x2.
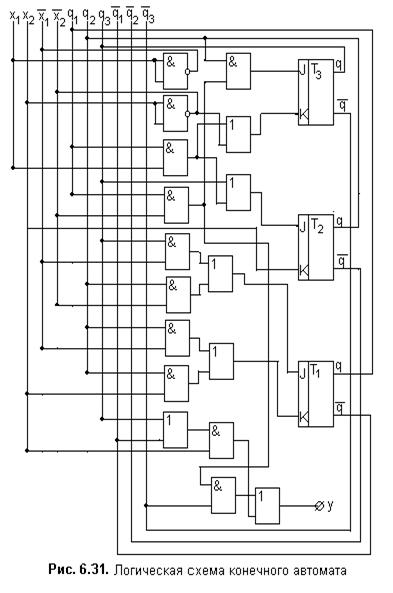
Принятые обозначения логических схем (см. рис. 6.25) и элементов временной задержки (см. рис. 6.27) позволяет составить логическую схему структурного автомата (см. рис. 6.19), опираясь только на минимальные ДНФ (или КНФ) операторов j и y для соответствующего типа триггера. На рис..6.31 приведена структура операторов j и y для JK-триггеров и минимальных ДНФ.
.3.3.3. Логическая схема автомата с “памятью”
Вопросы и задачи
6.1. Что такое "произведение автоматов"?
6.2. Что такое "сумма автоматов"?
6.3. Какие особенности в формировании "обратной связи"?
6.4. Автоматы М1 и М2 описаны таблицами поведения:
| Автомат М1 | Автомат М2 | |||||
| q1iÎQ1 | x1iÎX1 | q2jÎQ2 | x2jX2 | |||
| q10 | q10;1 | q11;0 | q20 | q20;0 | q21;1 | |
| q11 | q11;0 | q12;1 | q21 | q21;1 | q22;0 | |
| q12 | q12;1 | q13;0 | q22 | q22;0 | q20;1 | |
| q13 | q13;0 | q10;1 |
a) cоставить таблицу поведения и начертить граф композиции автоматов по схеме, приведенной на рис.6.15;
b) cоставить таблицу поведения и начертить граф композиции автоматов по схеме, приведенной на рис. 6.16a);
с) составить таблицу поведения и начертить граф композиции автоматов по схеме, приведенной на рис. 6.16b);
d) cоставить таблицу поведения и начертить граф композиции автоматов по cхеме, приведенной на рис. 6.16c), при условии: если y2=0, то на выходе автомата М генерируется выходной символ автомата М1, если y2=1, то - выходной символ автомата М2;
e) cоставить таблицу поведения и начертить граф композиции автоматов по схеме, приведенной на рис. 1.29d), при условии: если y2=0, то на выходе автомата М генерируется выходной символ автомата М1, если y2=1, то - выходной символ автомата М2.
6.5. Каковы основные правила разметки блок-схемы алгоритма для моделирования автоматом Мили?
6.6. Каковы основные правила разметки блок-схемы алгоритма для моделирования автоматом Мура?
6.7. Выполнить разметку блок-схемы алгоритма, составить таблицы поведения и нарисовать графы для моделирования автома тами Мили и Мура:
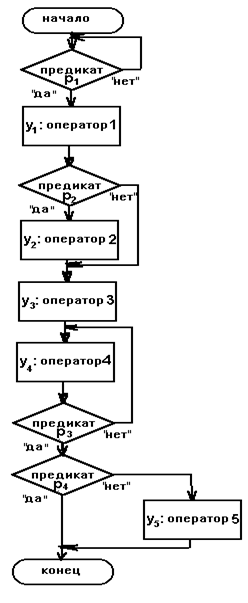
Литература
1. Алферова 3.В. Теория алгоритмов. - М.: "Статистика", 1973, 164 с.
2. Горбатов В. А. Основы дискретной математики: Учебное пособие. – М.: Высшая школа, 1986, 480с.
3. Горек5555батов В. А. Фундаментальные основы дискретной математики. Информационная математика.- М.: Наука. Физматлит, 2002, 544с.
5. Грей П. Логика, алгебра и базы данных. Пер. с англ./ Килова Х.И./ - М.: “Машиностроение”, 1989, 360c.
5. Евстигнеев В. А. Применение теории графов в программировании. – М.: Наука, 1985.
6. Кириллов В. И., Старченко А. А. Логика.- М.: Высшая школа, 1987.
7. Кузнецов О.М., Адельсон-Вельский Г.М. Дискретная математика для инженера. - М.: Энергоатомиздат, 1988, 480 с.
8. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов.- М.: Наука, 1975, 240 с.
9. Лихтарников Л. М., Сукачева В.М. Математическая логика. Курс лекций.- СПб.: Лань, 1998, 288с.
10. Математическая энциклопедия. Ред. коллегия: И.М. Виноградов (гл. ред.) T.I — М.: "Советская энциклопедия", 1977. — 1152 с.
11. Непейвода Н. Н. Прикладная логика: Учеб. Пособие.- 2-е изд., испр. и доп.- Новосибирск, изд-во Новосиб. Ун-та, 2000.-521с.
12.Новиков Ф. А. Дискретная математика для программистов. – СПб.: Питер. 2000, 304с.
13. Обработка нечеткой информации в системах принятия решений / А.Н. Борисов, А.В. Алексеев, Г.В. Меркурьева и др. – М.: Радио и связь, 1989, 304с.
14. Пономарев В.Ф. Дискретная математика для информатиков-экономистов. Учебное пособие. – Калиниград: КГТУ и КИМБ, 2002, 239с.
15. Сачков В.Н. Введение в комбинаторные методы дискретной математики.-М.: Наука, 1982, 384 с.
16. Филлипс Д, Гарсиа-Диас А. Методы анализа сетей.-М.: Мир, 1984, 496 с.
Предметный указатель
автомат, 279
абстрактный, 279
автономный, 285
вероятностный, 282
детерминированный, 282, 287
инициальный, 282
комбинационный, 286
конечный, 279
микропрограммный, 304
Мили, 283
минимальный, 313
Мура, 283
недетерминированный, 282, 287
операционный, 296
порождающий, 285
распознающий, 285
структурный, 279, 333
управляющий, 296
аксиома
ассоциативности, 29
дистрибутивности, 29
идемпотентности, 29
коммутативности, 29
поглощения, 29
алгебра
булева, 28
высказываний,159
множеств
четких,51
нечетких, 63общая, 28
реляционная, 216
алгоритм
Дейкстра, 130
Краскала, 132
минимизации автомата детерминированного, 315
недетерминированно-
го, 327
нормальный Маркова, 242
поиска неизвестного множества, 62
преобразования формулы
к виду СДНФ, 44
к виду СКНФ, 45
приведения формулы
к ССФ, 197
к ПНФ, 195
принципа резолюции, 182
Флойда, 134
Форда-Фалкерсона, 143
булеан, 13
валентность вершины, 92
вершина графа, 91
смежная, 93
исток, 92
сток, 92
вершинная связность, 94
выборка, 78
грань
верхняя, 28
нижняя, 28
граф, 91
вершинно-взвешенный, 98
взвешенный, 98
двудольный, 98
дополнительный, 93
планарный, 97
плоский, 97
полный, 93
пустой, 93
реберно-взвешенный, 98
связный, 93
суграф, 97
типа дерево, 94
частичный, 97
законы алгебры
булевой, 30
высказываний, 167
множеств, 58
предикатов, 194
знак
включения, 12
невключения, 13
непринадлежности, 12
принадлежности, 12
строгого включения, 13
импликанта, 47
имплицента, 47
инциденция, 92
квантор
всеобщности, 188
существования, 188
класс состояний,
неотличимых 308
отличимых, 313
совместимых, 308
согласованных, 329
эквивалентных, 308
компонента кортежа, 15
конфигурация
машины Тьюринга, 251
кортеж, 14
совместимый, 15
маршрут
гамильтонов, 96
замкнутый, 95
открытый, 95
эйлеров, 96
матрица
весов, 102
достижимости, 103
инциденции, 100
разрезов, 104
смежности, 101
машина Тьюринга, 242
метод
дедуктивного вывода, 173
критического пути, 147
микрокоманда, 304
микрооперация, 304
минимизация
ДНФ, 48
КНФ, 50
множество, 11
нечеткое, 11
пустое, 13
счетное, 12
универсальное, 13
четкое, 11
моделирование
алгоритмов, 295
мощность множества, 12
нормальная форма формулы
дизъюнктивная, 43
конъюнктивная, 45
область
значений, 19
определения, 19
отправления, 19
прибытия, 19
образ, 19
объект
алгоритмический, 241
комбинаторный, 78
оператор
автоматный, 282
выбора, 218
деления, 224
дополнения, 220
естественного соединения, 223
объединения, 221
пересечения, 222
поведения, 280
проекции, 219
прямого произведения, 222
разности, 222
соединения, 223
операции
бинарные, 29
унарные, 29
операция
дизъюнкции, 29, 30
конъюнкции, 29, 30
отрицания, 30
рекурсии, 244
суперпозиции, 243
остов, 97
отношение, 24
антисимметричное, 26
антррефлексивное, 25
асимметричное, 26
бинарное, 24
рефлексивное, 25
симметричное, 26
строгого порядка, 27
транзитивное, 26
унарное, 24
частичного порядка, 26
четкое, 24
эквиваленции, 26
отображение, 18, 19
гомоморфное, 307
изоморфное, 308
переменная
лингвистическая, 17
пропозициональная, 158
свободная, 189
связанная, 189
переменная-кортеж
свободная, 225
связанная, 225
перестановка элементов, 80
подграф, 96
подмножество, 12
правила
введени связок, 174
включения-исключения, 85
заключения, 204
замещения, 31
произведения, 84
суммы, 84
предикат, 21
принцип резолюции, 182
произведение автоматов, 334
прообраз, 19
путь критический, 146
разрез графа, 95
ребро смежное, 93
режим
асинхронный, 333
синхронный, 333
свойства алгоритмов, 241
связки логические, 159
связность
сильная, 93
слабая, 93
связь обратная, 339
семейство подмножеств, 13
сигнатура алгебры, 29
символы
нетерминальные, 250
терминальные, 250
соответствие, 18, 19
сочетание элементов, 81
степень
вершины графа, 92
принадлежности, 16
суждение
общее, 188
частное, 188
сумма автоматов, 340
схема
дедуктивного вывода, 178
примитивной рекурсии, 244
реляционной базы, 215
таблица истинности, 163
терм, 190
терм-множество, 17
формула
выводимые, 173
предваренная нормальная, 195
тождественно истинные, 173
тождественно ложные, 173
функция булева, 20
вырожденная, 34
линейная, 38
монотонная, 38
невырожденная, 34
-повторитель, 32
самодвойственная, 37
сохраняющая "0", 40
сохраняющая "1", 40
функция
высказывательная, 187
выхода, 280
константа, 243
общерекурсивная, 242
переходов, 280
предшествования, 245
принадлежности, 16
рекурсивная, 242
следования, 243
тождества, 243
усеченного вычитания, 246
частично рекурсивная, 242
число
комбинаторное, 78
компонент связности, 106
неплотность, 108
плотность, 108
Стирлинга, 82
хроматическое, 108
цикломатическое, 106
эквивалентность
автоматов, 307
Экспертные системы, 233
|
|
|


