Порядок проведения работы.

Брус нагружается начальной нагрузкой для устранения зазоров в установке и в таблицу записывают соответствующие показания тензорезисторов. Затем брус нагружается силами и записываются показания тензорезисторов при этих нагрузках. Установка разгружается. По данным таблицы вычисляются величины приращения деформаций, а затем величины приращения напряжений по формуле:

где, ∆n_{i -} средняя разность показании тензорезисторов

K - цена деления прибора.

 

Рис. 25

Производится расчет величины приращений напряжений для ступени нагрузки Р по формуле:

σ – нормальное натяжение в брусе

P- величина ступени нагрузки

A- площадь поперечного сечения бруса

Z_p- координата точки приложения нагрузки, M_y=PZ_p

Z_i -координата точки, для которой, определяется деформа­ция

_y - момент инерции поперечного сечения

Величины напряжений, полученные из опыта, сравниваем с их расчетными величина и вычисляется, расхождение результатов в процентах по формуле:

 

Таблица

НАГРУЗКА	Показания тензорезисторов
	n1	∆ n1	n2	∆ n2	n3	∆ n3
P
∆Р=	∆ n 1ср	∆ n2ср	∆ n3ср

 

 

 

Лабораторная работа № 12

ДЕМОНСТРАЦИЯ ТЕОРЕМЫ О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЙ

 

Теорема о взаимности перемещений широко используется при рассмотрении статически неопределимых систем.

Согласно этой теореме для двух одинаковых по величине гру­зовых состоянии Р₁, и Р₂ (рис. 26) перемещение по нап­равлению первой силы, вызванное второй — ∆₁₂ равно перемещению по направлению второй силы, вызванному первой - ∆₂₁

∆₁₂= ∆_21,

где, ∆₁₂ - перемещение по направлению силы 1 от действия силы 2

∆_{21 -} перемещение по направлению силы 2 от действия силы 1.

Рис. 26

Цель лабораторной работы состоит в демонстрации теоремы о взаимности перемещений и сравнении результатов испытаний и расчета.

 

Порядок проведения работы

Схема установки для проведения работы показана на рис. 27. Для опыта используется стальная балка прямоугольного сечения, свободно лежащая на двух опорах. Установка допускает приложение нагрузки и измерение прогиба в любой точке' балки. Прогибы измеря­ются индикаторами часового типа с точностью до 0,01 мм.

Рис. 27

 

В точке 1 балки устанавливается подвеска с тарелкой, на ко­торую кладется груз Р₁. Индикатор устанавливается в точке 2, чтобы при нагружении балки силой P₁ его и верительный стержень постоянно находится в соприкосновении с поверхностью балки. Наг­ружая балку в точке 1 силой P₁, замеряют прогиб ∆₂₁ в точке 2 и записывают результат. Затем прикладывают силу Р₂ в точку 2, а индикатор перекосят в точку 1, и записывают результат измере­ния ∆₁₂. Опит повторяют несколько раз.

Полученные средние значения прогибов ∆₁₂ и ∆₂₁ в соответст­вии со свойством взаимности должны быть равны.

 

Расчетная часть работы

Теоретические значения прогибов ∆₁₂ и ∆₂₁, можно определить с помощью различных методов, например, используя метод начальных параметров. Для применения этого метода предварительно нужно оп­ределить реакцию опоры R_А в точке А на левом конце балки при нагружении ее по первому или второму состоянию.

Для. случая нагружения балки только сосредоточенными силами уравнение метода начальных параметров примет вид:

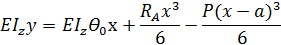
где, - жесткость балки на изгиб,

- прогиб балки в произвольной точке, отстоящей на расстоянии х от начала координат (опо­ра А),

Для определения начального параметра используем условие отсутствия прогиба в точке В, т.е. при х=l, y_B=0. Отсюда, применяя уравнение получим:

;

 

Для стальной балки модуль упругости Е = 2*10⁶ кг/см². Дли­на пролета балки l, размеры а₁ и а₂ определяются непосредственными измерениями. Для вычисления момента инерции прямоугольного сечения балки надо замерить также высоту h ширину b в сечении и определить Y_z по формуле .

Рис. 27

 

Для первого состояния упругой балки (рис.27a) можно записать уравнение статики:

∑M_B=0; R'_Al – P₁ (l-a₁) = 0;

Для х = а₂ прогиб у= ∆₂₁.Из предыдущих уравнений следует:

Решая эту систему уравнений совместно, молено определить величину . Для второго состояния упругой балки (рис.27б) из уравнения статики определяется реакция R''_A.

∑M_B=0; R''_Al – P₂ (l-a₂) = 0;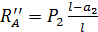

Для х = а₁ прогиб у= Σ₁₂ и уравнения примут вид:

Решая, эту систему уравнений, определяют величину .

Расчетные значения прогибов а и по свойству взаимности перемещений должны быть равны.

Значения прогиба Σ_теор и _Σэксп полученные расчетными и экспериментальными путями, следует сравнить между собой и оценить погрешность по формуле

 

 

Лабораторная работа № 13

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: