 |
Определение горизонтальной реакции опоры и напряжений в статически неопределимой раме
|
|
|
|
В этой работе рассматривается простейшая 1 раз статически неопределимая стержневая рама с участками постоянной жесткости(рис. 31),имеющая 2 шарнирно-неподвижные опоры и нагруженная по горизонтальному стержню двумя сосредоточенными силами Р.
Целью работы является экспериментальное определение горизонтальной реакции опоры, нормальных напряжений в горизонтальном стержне рамы и сравнение полученных результатов с теоретическими.
 Рис. 31.
Рис. 31.
Экспериментальная часть задачи.
Экспериментальная часть
задачи выполняется на установке, показанной на рис.32 и состоящей из следующих основных частей:
-
| Рис. 31 |
- устройство 5 для определения величины горизонтальной реакции;
- индикатора 6 часового типа;
- двух подвесов 7 для нагружения рамы;
- шести тензорёзисторов наклеенных посередине пролета рамы 4 которые попарно присоединены к тензостанции, причем три тензорезистора на верхней и три на нижней поверхности горизонтального участка рамы.

Рис. 32
При нагружении рамы сосредоточенными нагрузками шарнирно-подвижная опора получает перемещение в горизонтальном направлении, величина которого измеряется индикатором часового типа с ценой деления 0,01 мм. Устройство для определения величины горизонтальной реакции показано на рис.40 и состоит из рычага 9, уравновешиваемого относительно оси поворота 12 противовесом 10 и стержня 11.
длиной l1, соединенного с подвижной опорой (4) исследуемой рамы. Перемещая противовес по горизонтальному рычагу модно создать имитацию шарнирно-подвижной опоры. Это состояние характеризуется возвращением стрелки индикатора (6) в исходное положение, т. е. на ноль.
|
|
|

Рис. 33
Величина горизонтальной реакции X, возникающая при имитации шарнирно-неподвижной опоры, может быть определена из условия -равновесия моментов сил относительно точки О
∑М0 = Xl1 –P прот *C = 0
Отсюда: X= Pпрот 
где, P прот - вес противовеса, равный 1 кг,
l1 – длина стержня 2, равная 6 см,
с – плечо противовеса, отсчитываемого по горизонтальному рычагу в см.
Поэтому формула X= Pпрот  примет вид:
примет вид:
X = 1* 
В момент нагружения рамы грузами, противовес должен быть расположен на оси поворота рычага, т.е. против нулевого деления шкалы рычага.
Эксперимент проводится в следующем порядке:
В соответствии с заданной преподавателем расчетной схемой (рис. 33) подготовить установку.
Провести измерение расстояний a, bl рамы и h, b1 поперечного сечения горизонтального пролета рамы. (рис. 34)
Установить противовес против нулевого деления и стрелку индикатора часового типа на 0.
Включить тензостанцию и снять показания тензорезисторов при Р = 0.
Нагрузить раму заданной нагрузкой Р.
Зафиксировать величину горизонтального перемещения подвижной опоры ∆Р, затем сместить противовес из исходного нулевого положения, которое соответствует возвращению стрелки индикатора на 0 и определить по шкале горизонтального рычага величину С.
Снять показания тензорезисторов и записать в таблицу:
Таблица
| НАГРУЗКА | Показания тензорезисторов | ||||||
| n1 | ∆ n1 | n2 | ∆ n2 | n3 | ∆ n3 | ||
| P | |||||||
| ∆Р= | ∆ n 1ср | ∆ n2ср | ∆ n3ср |
Здесь Σn1- разность показаний тензорезисторов 1, 2 и 3 под нагрузкой Р и при Р = О, Σ/2 - среднее показание
|
|
|
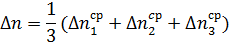
По окончанию опыта раму разгрузить, а противовес установить в нулевое положение.
По формуле X = 1*  определить величину горизонтальной реакции Xтеор. и сравнить с расчетной величиной X эксп. по формуле
определить величину горизонтальной реакции Xтеор. и сравнить с расчетной величиной X эксп. по формуле
 *100%
*100%
10. Определить экспериментальное значение нормальных напряжений от изгиба в середине пролета по формуле
σэксп = 
| Рис. |
Расчетная часть задачи.
Наиболее широко применяемым методом раскрытия статической неопределимости стержневых и рамных систем является метод сил. В этом методе заданная статически неопределимая система освобождается от дополнительных связей и их действие заменяется силами или моментами, величины которых подбираются так, чтобы перемещения соответствовали тем ограничениям, которые накладываются на систему отброшенными связями.
| Рис. 34 |
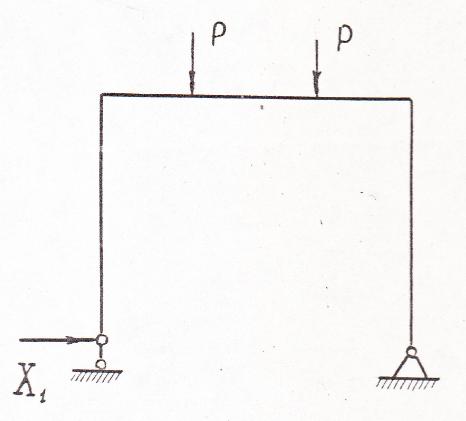
Система, освобожденная от дополнительных связей, становится статически определимой и называется основной системой. В качестве дополнительной связи для рассматриваемой рамы будет считать горизонтальную связь на левой опоре (рис. 41). По направлению отброшенной связи прикладываем её реакцию - неизвестное усилие X1. Каноническое уравнение метода сил показывает, что полное перемещение в основной системе, возникающее по направлению неизвестного усилия Σ, под влиянием силы и заданной нагрузки Р, равно нулю:
δ11Х1+∆1Р=0
Для определения коэффициентов δ11 и ∆1Р каноническое основная система (рис. 35) поочередно нагружается единичным горизонтальным усилием 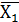 = 1 (рис. 36) и заданной нагрузкой Р (рис. 43). Для каждого вида нагружения строятся эпюры от единичной нагрузки
= 1 (рис. 36) и заданной нагрузкой Р (рис. 43). Для каждого вида нагружения строятся эпюры от единичной нагрузки 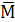 ,и грузовая МР. Путем перемножения эпюры
,и грузовая МР. Путем перемножения эпюры 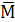 саму на себя и на грузовую эпюру МР по правилу Верещагина определяются коэффициенты канонического уравнения.
саму на себя и на грузовую эпюру МР по правилу Верещагина определяются коэффициенты канонического уравнения.
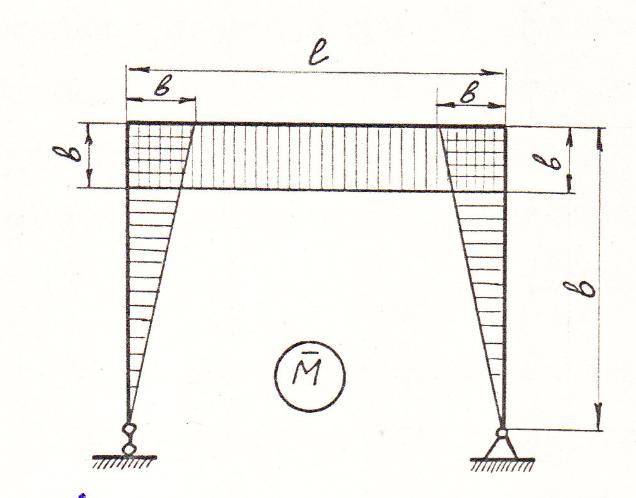

Рис. 35 Рис. 36
 ;
;
 .
.
Подставляя  и
и 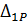 в уравнение σ11Х1+Σ1Р=0, получим:
в уравнение σ11Х1+Σ1Р=0, получим:

Отсюда

 Рис. 37
Рис. 37
Входящие сюда величины a, b, l получают непосредственными измерениями на раме, подготовленной для проведения эксперимента. При заданной величине a по формуле 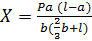 определяют горизонтальное усилие X1. Для получения окончательной суммарной эпюры изгибающих моментов ординаты единичной эпюры
определяют горизонтальное усилие X1. Для получения окончательной суммарной эпюры изгибающих моментов ординаты единичной эпюры 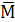 умножаются на найденное значение X1 и складываются с соответствующими ординатами грузовой эпюры МР моментов (рис. 37). Отсюда видно, что наибольшие изгибающие моменты Мmaxвозникают на среднем участке горизонтального стержня рамы и соответствующие нормальные напряжения на Рис. 44 участке рамы,определяемые теоретическим путем, будут
умножаются на найденное значение X1 и складываются с соответствующими ординатами грузовой эпюры МР моментов (рис. 37). Отсюда видно, что наибольшие изгибающие моменты Мmaxвозникают на среднем участке горизонтального стержня рамы и соответствующие нормальные напряжения на Рис. 44 участке рамы,определяемые теоретическим путем, будут
|
|
|
 ,
,
 - изгибающий момент в середине полета рамы,
- изгибающий момент в середине полета рамы,  - осевой момент
- осевой момент
сопротивления.
Для прямоугольного сечения высотой h и шириной b1 (рис. 37) 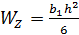 .
.
Входящие сюда величины 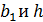 получают непосредственными замерами высоты и ширины горизонтального пролета рамы.
получают непосредственными замерами высоты и ширины горизонтального пролета рамы.
| b |
| y |

(рис.38)
СОДЕРЖАНИЕ
ЛАБОРАТОРАНАЯ РАБОТА №1. «Определение механических характеристик стали при растяжении»……………………………………….....2
ЛАБОРАТОРАНАЯ РАБОТА №2. «Определение механических характеристик пластичных и хрупких материалов при сжатии» ………........12
ЛАБОРАТОРАНАЯ РАБОТА №3. «Экспериментальное определение деформаций и напряжений»……………………………………………….....…15
ЛАБОРАТОРАНАЯ РАБОТА №4. «Определение модуля продольной упругости и коэффициента Пуассона»…………………………………….......22
ЛАБОРАТОРАНАЯ РАБОТА №5. «Определение предела прочности материала при срезе»………………………………………………………........24
ЛАБОРАТОРАНАЯ РАБОТА №6. «Определение главных напряжений при кручении тонкостенной трубы»………………………………………..............27
ЛАБОРАТОРАНАЯ РАБОТА №7. «Определение напряжения в балке при изгибе»……………………………………………………………………….......30
ЛАБОРАТОРАНАЯ РАБОТА №8. «Определение деформаций балки при изгибе»……………………………………………………………………….......35
ЛАБОРАТОРАНАЯ РАБОТА №9. «Определение деформаций консольной балки при изгибе»…………………………………………………………....….38
ЛАБОРАТОРАНАЯ РАБОТА №10. «Определение перемещений балки при косом изгибе»…………………………………………………………............…41
ЛАБОРАТОРАНАЯ РАБОТА 11. «Определение напряжений в брусе при внецентренном растяжении»……………………………………………....…...43
ЛАБОРАТОРАНАЯ РАБОТА 12. «Демонстрация теоремы о взаимности перемещений»……………………………………………………………....…...46
|
|
|
ЛАБОРАТОРАНАЯ РАБОТА 13. «Определение момента в защемлении статически неопределимой балки»………………………………………....….50
ЛАБОРАТОРАНАЯ РАБОТА 14. «Определение горизонтальной реакции опоры и напряжений в статически неопределимой раме»……………….......55
|
|
|


