 |
Уравнение электронейтральности
|
|
|
|
Рассмотрим более подробно связь между напряжением на затворе VG МДП-структуры и поверхностным потенциалом ψs. Все приложенное напряжение VG к МДП-структуре делится между диэлектриком и полупроводником, причем очевидно, что падение напряжения в полупроводнике равняется поверхностному потенциалу ψs.
Таким образом,
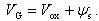(2.42)
Из (2.42) и анализа зонных энергетических диаграмм на рисунке 2.10 следует, что знак поверхностного потенциала ψs, выбранный нами ранее a priori, в действительности соответствует знаку напряжения на затворе VG. Действительно, положительное напряжение на затворе идеальной МДП-структуры вызывает изгиб зон вниз у полупроводников n- и p-типа, что соответствует положительным значениям поверхностного потенциала. Отрицательное напряжение VG вызывает изгиб зон вверх у поверхности полупроводника, что соответствует отрицательному значению поверхностного потенциала ψs.
Из условия электронейтральности следует, что заряд на металлическом электроде QM должен быть равен суммарному заряду в ОПЗ Qsc, заряду поверхностных состояний на границе раздела полупроводник-диэлектрик Qss и встроенному заряду в диэлектрик вблизи границы раздела Qox.
Тогда
(2.43)
Согласно определению геометрической емкости диэлектрика Cox,
(2.44)
отсюда
(2.45)
Учитывая, что между металлом и полупроводником существует разность термодинамических работ выхода Δφms, получаем:
(2.46)
Из соотношения (2.45) следует, что если VG > 0, то ψs > 0, величины Qsc < 0, Qss < 0, т.е. падение напряжения на диэлектрике Vox > 0. Аналогично будет соотношение знаков и при VG < 0. Поскольку нами было показано ранее, что
(2.47)
подставив (2.47) в (2.46), имеем:
(2.48)
Введем новое обозначение - напряжение плоских зон VFB (Flat Band). Напряжением плоских зон VFB называется напряжение на затворе реальной МДП-структуры, соответствующее значению поверхностного потенциала в полупроводнике, равному нулю:
|
|
|
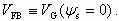(2.49)
С учетом определения (3.82) из (3.81) следует:
(2.50)
Таким образом, связь между напряжением на затворе VG и поверхностным потенциалом ψs с учетом (2.50) задается в виде:
(2.51)
Проведем более подробный анализ (2.51) для различных областей изменения поверхностного потенциала.
Обогащение (ψs < 0)
Выражение для заряда в ОПЗ Qsc описывается соотношением (2.19). Подставляя (2.19) в (2.42), получаем:
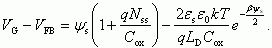(2.52)
Для больших значений ψs(
), когда Qsc >> Qss, из соотношения (2.52) следует:
(2.53)
Отсюда
(2.54)
Из (2.53) и (2.54) следует, что при обогащении поверхности дырками, как основными носителями, поверхностный потенциал ψs зависит от напряжения на затворе VG логарифмически, а заряд Qsc в ОПЗ зависит от напряжения на затворе VG линейно.
Обеднение и слабая инверсия (0 < ψs < 2φ0)
Заряд в ОПЗ Qsc в этом случае в основном обусловлен ионизованными акцепторами QB и выражается соотношением (3.20).
Разложим выражение для QB в ряд вблизи ψs = φ0:
здесь QB*, CB* - величина заряда и емкости ионизованных акцепторов в ОПЗ при ψs = φ0.
Подставив выражение для QB в (2.51) и учтя выражение для CB* (3.57), получаем:
(2.55)
где
(2.56)
Из соотношения (2.55) следует, что в области обеднения и слабой инверсии поверхностный потенциал ψs зависит от напряжения VG линейно, причем тангенс угла наклона 
определяется плотностью поверхностных состояний Nss, толщиной подзатворного диэлектрика dox и уровнем легирования полупроводниковой подложки NA.
Сильная инверсия (ψs > 2φ0)
Заряд в ОПЗ Qsc отрицателен, состоит из заряда ионизованных акцепторов QB и электронов Qn в инверсионном слое. Учитывая выражение (3.22) для Qn, имеем:
(2.57)
где величина Δψs = ψs - 2φ0.
|
|
|
Введем пороговое напряжение VT как напряжение на затворе VG, когда в равновесных условиях поверхностный потенциал ψs равен пороговому значению 2φ0.
(2.58)
Из (2.57) и (2.58) следует, что
(2.59)
или с учетом определения VFB
(2.60)
Из (2.60) следует, что если отсчитывать пороговое напряжение VT от напряжения плоских зон VFB, то оно будет состоять из падения напряжения в полупроводнике 2φ0 и падения напряжения на подзатворном диэлектрике за счет заряда ионизованных акцепторов и заряда в поверхностных состояниях. Для достаточно высоких значений ψs, когда βΔψs > 1, имеем:
(2.61)
Отсюда
(2.62)
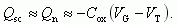(2.63)
Из (2.62) и (2.63) следует, что в области сильной инверсии, так же как и в области обогащения, поверхностный потенциал логарифмически зависит от напряжения на затворе VG, а заряд электронов в инверсионном слое Qn линейно зависит от величины VG.
На рисунке 2.15 приведена зависимость поверхностного потенциала ψs от напряжения на затворе VG, рассчитанная для различных толщин подзатворного диэлектрика dox.
Рис.2.15. Зависимость поверхностного потенциала ψs от напряжения на затворе VG, рассчитанная из уравнения (3.84) для кремниевой МДП-структуры с различной толщиной подзатворного диэлектрика
Емкость МДП-структур
Одним из наиболее распространенных методов изучения свойств структур металл - диэлектрик - полупроводник является метод, основанный на анализе зависимости емкости МДП-структуры CМДП от напряжения на затворе VG, так называемый метод вольт-фарадных характеристик (ВФХ) или C-V метод. Для использования этого метода рассмотрим подробно теорию емкости МДП-структур. В дальнейшем величину удельной емкости МДП-структуры будем просто обозначать меткой C без индексов. Согласно определению емкости,
(2.64)
Используя выражения для заряда на затворе QM из (2.44 и для падения напряжения на диэлектрике Vox из (2.42), получаем:
(2.65)
Таким образом, зависимость C МДП-структуры от напряжения будет определяться полученной нами ранее зависимостью ψs(VG), приведенной на рисунке 3.12. Сразу же можно из анализа (2.53) и (2.65) сказать, что в области сильной инверсии и обогащения емкость C будет слабо зависеть от величины VG, выходя на насыщение при больших VG. В области обеднения и слабой инверсии следует ожидать, участка с почти постоянной величиной емкости. Общая зависимость емкости от напряжения будет иметь вид кривой с ярко выраженным минимумом.
|
|
|
Воспользуемся выражением (2.51) для напряжения на затворе VG и продифференцируем (2.46) по ψs.
(2.66)
где Css, Csc - емкость поверхностных состояний и емкость ОПЗ, определенные ранее.
Подставляя (2.66) в (2.65) и проводя преобразования, получаем:
(2.67)
или
(2.68)
Соотношение (2.68) позволяет нам построить эквивалентную схему МДП-структуры, представив ее как последовательно соединенную емкость диэлектрика Cox с параллельной цепочкой емкости ОПЗ Csc и поверхностных состояний Css.
На рисунке 2.16 приведена эквивалентная схема емкости МДП-структуры. Отметим, что такую схему можно было нарисовать исходя из общих соображений об устройстве МДП-структур.
Рис. 2.16. Простейшая эквивалентная схема МДП-структуры
На рисунке 2.17 приведены равновесные C-V кривые идеальных МДП-структур с разной толщиной диэлектрика, рассчитанные по уравнению (2.76).
Рис. 2.17. Равновесные C-V характеристики идеальных МДП-структур на кремнии p-типа с различной толщиной подзатворного диэлектрика
|
|
|
