Определение плотности поверхностных состояний на границе раздела полупроводник - диэлектрик

 

Методы вольт-фарадных характеристик дают несколько возможностей для определения величины и функции распределения плотности поверхностных состояний в запрещенной зоне полупроводника на границе раздела полупроводник - диэлектрик. Рассмотрим более подробно эти методы.

Дифференциальный метод

Дифференциальный метод, или метод Термана, основан на сравнении экспериментальной высокочастотной емкости МДП-структуры с теоретической расчетной емкостью идеальной МДП-структуры с такими же величинами толщины окисла и легирующей концентрации в подложке. На рисунке 2.22а приведены для иллюстрации метода расчета экспериментальная и расчетные C-V кривые.

Рис. 2.22. Расчет плотности поверхностных состояний дифференциальным методом: а) экспериментальная и теоретическая ВФХ для МДП-системы Si-SiO₂-Al; б) зависимость сдвига напряжения ΔV_G от поверхностного потенциала ψ_s, полученная из сечения постоянной емкости C = const МДП-структуры; в) зависимость плотности ПС от энергии E в запрещенной зоне полупроводника, полученная графическим дифференцированием кривой ΔV_G(ψ_s) по уравнению (2.82)

 

Поскольку емкость высокочастотная, то ее величина определяется только значением поверхностного потенциала ψ_s. Проведя горизонтальные сечения C = const, мы на экспериментальной кривой производим расстановку поверх-ностного потенциала ψ_s.

Сравнивая теперь величины напряжений на затворе V_G теоретической и экспериментальных C-V кривых, соответствующих одной и той же емкости (а следовательно, и одному значению поверхностного потенциала ψ_s), получаем из (2.51):

(2.81)

Графическим дифференцированием кривой (3.114) получаем:

(2.82)

Метод, основанный на анализе соотношения (2.81), довольно широко распространен, прост и не требует громоздких выкладок. К недостаткам этого метода необходимо отнести тот факт, что зависимость плотности поверхностных состояний N_ss от энергии E получается только в одной половине запрещенной зоны вблизи уровня Ферми. На рисунке 2.22б приведен график ΔV_G(ψ_s), а на рисунке 2.22в - распределение плотности поверхностных состояний в зависимости от энергии в запрещенной зоне полупроводника, полученное из предыдущего графика путем дифференцирования.

Интегральный метод

Интегральный метод, или метод Берглунда, основан на анализе равновесной низкочастотной вольт-фарадной характеристики. Поскольку для равновесной низкочастотной C-V кривой справедливо (2.65), то

(2.83)

Интегрируя соотношение (3.116) с граничными условиями ψ_s = ψ_si, V_G = V_Gi, получаем:

(2.84)

Поскольку C(V_G) - это экспериментальная кривая, то интегрирование уравнения (2.84) (потому метод и назван интегральным) сразу дает связь между поверхностным потенциалом и напряжением на затворе V_G. Выбор значений ψ_s1 и V_G1 произволен. Обычно величину ψ_s1 выбирают равной нулю (ψ_s1 = 0) и соответственно V_G1 - это напряжение плоских зон V_FB. Эти значения берутся из высокочастотных C-V кривых. Так как известна связь V_G(ψ_s), то из равенства (2.66) после нескольких преобразований следует:

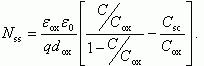(2.85)

Соотношение (2.85) позволяет определить величину и закон изменения плотности поверхностных состояний по всей ширине запрещенной зоны, что является преимуществом интегрального метода по сравнению с дифференциальным.

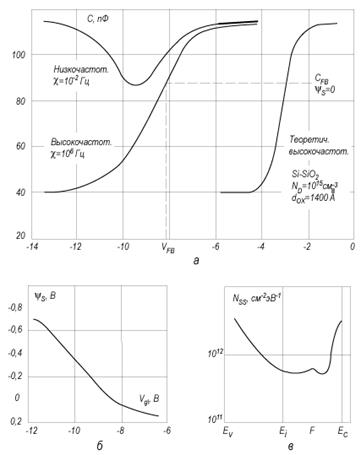
Рис. 2.23. Расчет плотности поверхностных состояний интегральным методом:
а) экспериментальная равновесная ВФХ МДП-системы Si-SiO₂-Al; б) зависимость поверхностного потенциала ψ_s от напряжения V_G, рассчитанная из этой кривой по уравнению (2.84); в) зависимость плотности ПС от энергии E в запрещенной зоне полупроводника, рассчитанная из уравнения (2.84) по этим экспериментальным данным

 

Из соотношения (2.84) следует, что численное интегрирование функции (1 - С/Сox) должно дать величину площади над равновесной C-V кривой. Поскольку емкость выходит на насыщение C → C_ox при примерно одинаковых значениях поверхностного потенциала, то следует ожидать, что у кривых с разной плотностью поверхностных состояний площадь под кривой C-V будет одинакова. На рисунке 3.20а,б, в приведены этапы расчета равновесных C-V кривых и даны соответствующие графики.

Температурный метод

Температурный метод, или метод Грея - Брауна, основан на анализе изменения напряжения плоских зон V_FB МДП-структуры при изменении температуры T. При изменении температуры полупроводника меняется объемное положение уровня Ферми.

Закон изменения φ₀(T), а следовательно и φ₀(E), известен и в области полной ионизации примеси довольно прост. Из выражения (2.50) для напряжения плоских зон V_FB следует, что при изменении температуры

(2.86)

 

Графическое дифференцирование соотношения (3.119) приводит к выражению для N_ss:

(2.87)

Основным достоинством температурного метода является тот факт, что этим методом возможно получить величину плотности поверхностных состояний N_ss вблизи краев запрещенной зоны. К недостаткам метода следует отнести необходимость измерений в широком интервале температур T = (77÷400) К и трудность расчета, а также необходимость выполнения критерия высокочастотности в широком диапазоне температур. На рисунке 2.24а, б, в приведены экспериментальные C-V кривые, их изменение с температурой и результаты расчета.

Рис.2.24. Расчет плотности поверхностных состояний температурным методом:
а) экспериментальные высокочастотные ВФХ МДП-структур Si-SiO₂-Al при разных температурах T; б) зависимость измерения напряжения плоских зон ΔV_FB и положения уровня Ферми φ₀ в объеме полупроводника от температуры; в) зависимость плотности ПС N_ss от энергии E в запрещенной зоне полупроводника, рассчитанная из уравнения (2.87) по этим экспериментальным данным

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: