Уравнения в частных производных

Из математики и физики известны случаи аналитического описания систем с распределенными параметрами уравнениями в частных производных. Ими являются уравнения диффузии, тепломассопереноса и другие. Рассмотрим варианты их имитации на компьютере.

Еще раз напомним, что системы с распределенными параметрами — это системы, в которых значение некоторого изучаемого параметра изменяется не только во времени, но и в пространстве (одно-, двух- или многомерном), меняясь от точки к точке пространства по какому-то закону. Примером такого параметра может служить энергия, концентрация вещества, напряженность поля и другие физические величины. Неизменным изучаемый параметр может считаться только в бесконечно малой области пространства. Поэтому систему с распределенными параметрами часто представляют как систему из упорядоченного в пространстве множества элементов, внутри которых (в каждой точке отдельного взятого элемента) описываемый параметр одинаков, а у разных элементов различен. Элементы системы образуют пространственную структуру.

В качестве примера приведем проект для изучения теплопроводности стены дома. На рис. 19.1 представлена реализация такой системы в среде «Stratum-2000». Схема собрана из элементов (имиджей). Элементы двухмерной системы имитируют кирпичи, из которых сложена стена. На рис. 19.1 видны кирпичи, сделанные из разного материала (что обозначено желтым, голубым, красным цветами) и уложенные в определенном порядке, что, по мнению автора схемы, улучшает теплоизоляцию помещения. Серые и зеленые элементы на краях стены задают краевые условия, имитируя окружающую среду. Рядом показано для примера, как элементы в такой системе связаны друг с другом. По связям соседние элементы в процессе расчета обмениваются информацией между собой о температуре. Заметим, что в данном проекте, который имеет вид конструктора, пользователь схемы может менять параметры элементов системы, условия, конструкцию стены, порядок укладки (топологию), что при решении задачи аналитическими методами крайне затруднительно и требует применения методов моделирования.

Рис. 19.1. Двухмерная система с распределенными параметрами для исследования свойств теплопроводности стены дома

Существуют типовые уравнения, описывающие отдельные свойства систем с распределенными параметрами. Рассмотрим их.

Уравнение диффузии

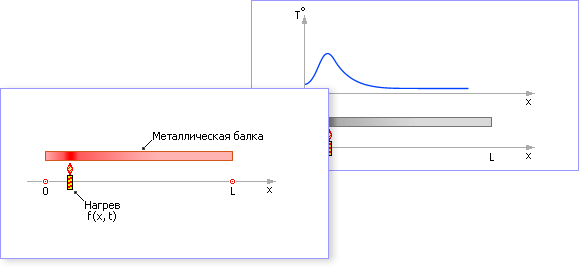
Уравнение диффузии описывает распространение (растекание) со временем по протяженному телу некоторой субстанции, например, тепла или концентрации. В одномерном случае тело представляется протяженным вдоль оси x.

На рис. 19.2 показан пример распределения вдоль оси x такого параметра как температура T. Из обычного опыта хорошо известно, что в каждый момент времени t температура T на разных участках тела x имеет разные значения, то есть меняется в зависимости от участка и времени. То есть должен существовать закон, по которому изменяется величина этого параметра T как функции от (x, t). Для температуры этот закон чаще всего задается уравнением диффузии.

Рис. 19.2. Пример применения уравнения диффузии к описанию процесса нагрева протяженного одномерного тела

Если изменяемый параметр (в общем случае) обозначить как y, время, в течение которого отслеживаются изменения параметра, обозначить как t, а ось, вдоль которой происходят изменения параметра, как x, то уравнение диффузии имеет вид:

и обычно дополняется условиями — значениями переменной y на краях и границах: на левом краю x = 0, на правом краю x = L, на границе — начальные условия (t = 0):

y (x, 0) = f ₁(x),
y (0, t) = f ₂(t),
y (L, t) = f ₃(t),
где f ₁(x), f ₂(t) и f ₃(t) — заданные функции.

На рис. 19.3 представлен схематически вид области, для которой определены граничные и начальные условия. Функции f ₁(x), f ₂(t), f ₃(t) и само уравнение диффузии предопределяют поведение функции y (x, t) внутри этой области, чей полный вид обычно надо определить. Если на схеме дополнительно построить ось y (см. рис. 19.4), то визуально на рисунке можно отобразить и сам вид функций. На рисунке четко видно, что в углах схемы значения задаваемых функций должно совпадать.

Рис. 19.3. Схема задания начальных и краевых условий для систем с распределенными параметрами в осях x, t (пример)

 

Рис. 19.4. Схема задания начальных и краевых условий для систем с распределенными параметрами в осях x, t, y (пример)

Коэффициент α имеет смысл коэффициента теплопроводности; f (x, t) имеет смысл функции, описывающей работу источников и стоков тепла.

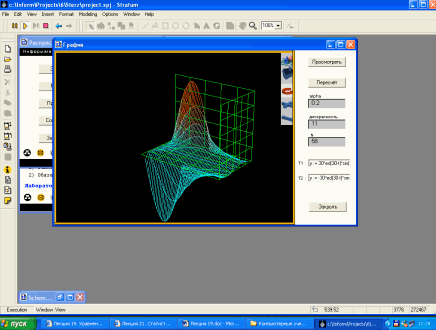
Величина y, описывающая распределение температуры, является функцией двух переменных — протяженности тела x и времени t: y (x, t). Графически функция представляется поверхностью (см. рис. 19.5) или набором изолиний (см. рис. 19.6), вид которых обычно требуется определить.

Рис. 19.5. Расчет распространения тепла в одномерном стержне со временем

 

Рис. 19.6. Распространение тепла по элементам двухмерной системы (расчет статической задачи, представленной на рис. 19.1). В отдельном окне видна оценка точности расчета в зависимости от количества итераций

Если заменить выражения производных их дискретным аналогом, то в разностном виде уравнение будет выглядеть так:

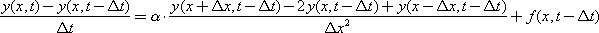
или, выражая неизвестное через известные величины:

или

В результате получена расчетная формула, реализуемая на цифровой вычислительной машине. Благодаря этой формуле можно рассчитать значение параметра y в любой точке (x, t).

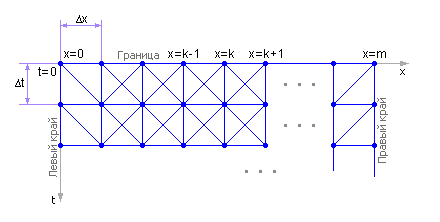
Назовем значение y (x, t) узлом расчета. Тогда схематично расчет выглядит как сетка узлов на поле, составленном из частей тела и отрезков времени (см. рис. 19.7). Сама формула расчета одного узла зависит от состояния трех узлов (левого y (x – Δ x, t – Δ t), правого y (x + Δ x, t – Δ t), собственного y (x, t – Δ t)) в предыдущий (t – Δ t) момент времени и напоминает треугольный шаблон. До начала расчета известны состояния всех узлов для t = 0. Применяя формулу последовательно ко всем узлам для следующего момента времени, можно определить температуру во всех узлах следующего временного слоя (t + Δ t). Кроме самого левого и самого правого узлов — их состояние вычислено быть не может, но оно задано краевыми условиями.

Рис. 19.7. Схема расчета одномерной динамической системы с распределенными параметрами методом конечных разностей с использованием явного шаблона

Если процедуру повторять, переходя от одной точки тела x к другой, и далее от одного временного слоя к другому, то по данной формуле можно вычислить значение температуры в любой части тела в любой момент времени. Таким образом, расчетом покрывается все поле (L x T) (см. рис. 19.7). Последовательное определение неизвестных значений в данном случае возможно, потому что шаблон имеет вид явного выражения — единственное неизвестное в формуле выражено через ранее вычисленные значения.

Заметим, что при больших значениях производных и больших значениях шагов расчет может дать неверные решения. Решения могут оказаться неточными или даже неустойчивыми (качественно неверными) (см. лекцию 10. «Численные методы интегрирования дифференциальных уравнений. Метод Эйлера»).

Условие устойчивости для треугольного шаблона при решении уравнения диффузии: Δ x /Δ t > α (см. подробнее рис. 19.12).

При моделировании возможно применение других разностных формул (шаблонов) (см. рис. 19.8). При выборе шаблона необходимо принимать во внимание: явный шаблон или нет, какую он обеспечивает точность и при каких значениях шагов он обеспечивает устойчивость расчета. Так, например, шаблон в виде прямоугольника — неявный: в одной расчетной формуле содержится сразу две неизвестные величины. Поэтому при использовании такого шаблона необходимо решать систему алгебраических уравнений размером (L · T).

Рис. 19.8. Схемы типовых шаблонов для решения уравнений с распределенными параметрами

На практике устойчивости, а далее — точности добиваются получением решений с использованием разных шаблонов и разных значений шага. Если значения искомой переменной, вычисленные с шагом h и с шагом h /2, отличаются в узлах с одинаковыми индексами не более чем на 1—5%, то вычисленное значение принимают за приближенное решение задачи. Иначе уменьшают шаг еще в два раза, и процедуру оценки повторяют. (Дополнительно см. лекцию «Умеем ли мы вычислять на компьютере?».)

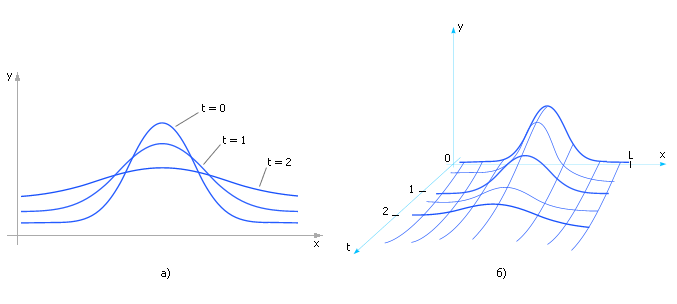
Свойства уравнения диффузии отражены на рис. 19.9 и заключаются в том, что при возникновении неоднородности в какой-то из частей тела со временем тепло за счет процессов теплообмена перетекает в соседние области. Температуры соседних областей выравниваются, усредняются. Темп процесса зависит от величины коэффициента теплопроводности.

Рис. 19.9. Характерный вид решения уравнения диффузии. На рисунке отражено изменение распределения параметра y вдоль оси x во времени. а) — в двух осях; б) — в трех осях

Если принять условие, что задача стационарная, то есть процессы протекают так долго, что все переходные процессы успели закончиться (производная по времени равна 0), то уравнение диффузии приобретает следующий вид (для случая двухмерного пространства — оси x и z) без источников и стоков:

∂² y /∂ x ² + ∂² y /∂ z ² = 0.

В разностном виде уравнение имеет вид:

(Y_{i + 1, j} – 2 · Y_{i , j} + Y_{i – 1, j} )/Δ x ² + (Y_{i , j – 1} – 2 · Y_{i , j} + Y_{i , j + 1})/Δ z ² = 0.

Если принять Δ x = Δ z, то уравнение примет вид:

4 · Y_{i , j} – Y_{i + 1, j} – Y_{i – 1, j} – Y_{i , j – 1} – Y_{i , j + 1} = 0.

Легко понять, что шаблон расчета уравнения неявный и имеет вид креста (чтобы рассчитать значение температуры в узле сетки, надо знать температуры его соседей слева, справа, сверху и снизу). Если стена дома имеет размеры 2 метра на 2 метра, а шаг Δ x = Δ z = 20 мм, то всего для расчета температурного режима стены придется решать систему из 10 000 линейных уравнений c 10 000 неизвестных Y_{i , j} :

4 · Y_{i , j} – Y_{i + 1, j} – Y_{i – 1, j} – Y_{i , j – 1} – Y_{i , j + 1} = 0, для i = 1÷100 и j = 1÷100,

к которым следует присоединить 400 штук краевых условий:
Y _{0, j} = f ₁(j);
Y _{101, j} = f ₂(j);
Y_{i , 0} = f ₃(i);
Y_{i , 101} = f ₄(i).

Вид решения уравнения показан на рис. 19.6.

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: