|
Формально-математический способ
|
|
|
|
Если реализовать модель на формальном языке, то запись будет выглядеть так, как показано ниже. Напомним, что данная нотация использует язык уравнений.
|
Уточненный метод Эйлера
Метод Эйлера для расчета дифференциальных уравнений имеет небольшую точность расчета. Как было показано ранее (см. Лекцию 10. Численные методы интегрирования дифференциальных уравнений. Метод Эйлера), точность расчета у него зависит от размера шага линейно, зависимость точности от шага — первой степени. То есть, чтобы увеличить точность в 10 раз, надо уменьшить шаг в 10 раз. На практике интересуются более совершенными методами. Вопрос стоит так: можно ли увеличить точность на порядок, но при этом сэкономить на количестве вычислений? Да, такие методы есть. Модифицированный метод Эйлера имеет точность второго порядка. В методе Эйлера производная берется в начале шага и по ней прогнозируется движение системы на конец шага, считая, что во время шага производная неизменна. То есть в течение всего шага производная считается той, какой она была в самом начале шага. Это основной источник неточности.
Улучшение метода состоит в том, что берется производная не в начале шага, а как промежуточное или среднее на разных участках одного шага. В разных вариантах метода вычисляют несколько производных в разных частях шага и усредняют их. Конечно, в этом случае число вычислений увеличивается, — но не в десятки раз, — а вот точность возрастает на порядок, в этом и состоит выигрыш.
Пусть, как и прежде (см. Лекцию 10. Численные методы интегрирования дифференциальных уравнений. Метод Эйлера), требуется решить уравнение y' = f (x, y, t). Идея уточненного метода Эйлера состоит в том, что производную вычисляют не в i -ой точке, а между двумя соседними точками: i и i + 1. Данная процедура состоит из следующих шагов:
|
|
|
- в точке i вычисляют значение производной:
f (xi, yi, t); - делают пол-шага и вычисляют значение функции на середине отрезка:
yi + 1/2 = yi + f (xi, yi, t) · Δ t /2; - в точке i + 1/2 вычисляют производную:
f (xi + 1/2, yi + 1/2, t + Δ t /2); - делается полный шаг из точки i в точку i + 1 по значению уточненной производной:
yi + 1 = yi + f (xi + 1/2, yi + 1/2, t + Δ t /2) · Δ t; - значение t увеличивается: t:= t + Δ t. Вся процедура повторяется сначала.
Данный метод обладает точностью Ο 2(h), то есть на порядок выше, чем метод Эйлера, при увеличении числа вычислений всего в 2 раза.
На рис. 14.1 показано, какой будет ошибка ε (расхождение между реальным и вычисленным теоретическим значением), если шаг делается по значению производной, вычисленной в точке i, как это делается в методе Эйлера. Эта ошибка может быть достаточно велика!
| |
| Рис. 14.1. Движение реальной и расчетной системы по методу Эйлера и расхождение между ними (ошибка) |
На рис. 14.2 показано, как по значению производной, вычисленной в точке i, делается полшага до точки t + Δ t /2 (направление производной показано линией A). И в точке t + Δ t /2 вычисляют новую производную. Касательная в точке t + Δ t /2 будет другой — линия B. Ее наклон равен производной в точке t + Δ t /2.
| |
| Рис. 14.2. Уточнение значения производной внутри шага расчета |
Далее переносят линию B обратно в точку t. Это соответствует тому, что из точки t снова делается, — но уже полный, — шаг Δ t до точки t + Δ t по направлению, соответствующему линии C (рис. 14.3). Линия C параллельна B. То есть значение производной в точке t берется искусственно равным производной в точке t + Δ t /2. Ошибка расчета (см. ε 1) во многих случаях при этом уменьшается.
|
|
|
| |
| Рис. 14.3. Движение реальной системы и системы, рассчитанной модифицированным методом Эйлера, и расхождение между ними (ошибка). На рисунке для сравнения показан результат, вычисленный по методу Эйлера |
Существует другой вариант модифицированного метода Эйлера, когда производную для того, чтобы сделать шаг из точки i, берут не в i -ой точке и не в i + 1/2, а как среднее арифметическое двух производных: производной в точке i (направление производной показано на рис. 14.4 линией A) и производной в точке i + 1 (направление производной показано линией B). Направление «средней» производной показано линией C.
| |
| Рис. 14.4. Расчет движения системы по среднему значению производной на шаге |
Метод Рунге-Кутты
Метод Рунге-Кутты используют для расчета стандартных моделей достаточно часто, так как при небольшом объеме вычислений он обладает точностью метода Ο 4(h).
Для построения разностной схемы интегрирования воспользуемся разложением функции

в ряд Тейлора:

Заменим вторую производную в этом разложении выражением

где
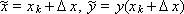
Причем Δ x подбирается из условия достижения наибольшей точности записанного выражения. Для дальнейших выкладок произведем замену величины «y с тильдой» разложением в ряд Тейлора:

Для исходного уравнения (1) построим вычислительную схему:

которую преобразуем к виду:

Введем следующие обозначения:

Эти обозначения позволяют записать предыдущее выражение в форме:

Очевидно, что все введенные коэффициенты зависят от величины Δ x и могут быть определены через коэффициент α, который в этом случае играет роль параметра:

Окончательно схема Рунге-Кутты принимает вид:

Та же схема в форме разностного аналога уравнения (1):
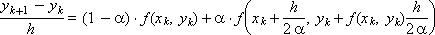
При α = 0 получаем как частный случай уже известную схему Эйлера:

При α = 1:

При α = 1 проведение расчетов на очередном шаге интегрирования можно рассматривать как последовательность нижеследующих операций.
1. Вычисляется выражение, представляющее собой полушаг интегрирования по схеме Эйлера, то есть определяется приближенное значение искомой функции в точке xk + h /2:

2. Для той же промежуточной точки находится приближенное значение производной:

3. Определяется уточненное значение функции в конечной точке всего шага, причем по схеме Эйлера с вычисленным на предыдущем шаге значением производной:
|
|
|

Геометрические построения (см. рис. 15.1) показывают, что получаемое в такой последовательности решение лежит «ближе» к истинному, чем вычисляемое по схеме Эйлера, то есть следует ожидать более высокой точности решения, получаемого методом Рунге-Кутты. Ранее мы назвали эту схему «модифицированным методом Эйлера».
| |
| Рис. 15.1. Иллюстрация расчета на шаге методом Рунге-Кутты при значении параметра α = 1 |
Теперь рассмотрим схему при α = 0.5 (геометрическая интерпретация результата приведена на рис. 15.2).

1. Выполняется полный шаг метода Эйлера с целью определения приближенного значения искомой функции на конце отрезка интегрирования:

2. Для этой же точки вычисляется приближенное значение производной:
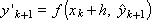
3. Находится среднее значение двух производных, определенных на концах отрезка:

4. Вычисляется значение искомой функции в конечной точке всего шага по схеме Эйлера с усредненным значением производной:

| |
| Рис. 15.2. Иллюстрация расчета на шаге методом Рунге-Кутты при значении параметра α = 0.5 |
Иногда получающееся выражение называют схемой (методом) Эйлера-Коши. Геометрически понятно, что получаемый указанным способом результат также должен быть «ближе» к истинному решению, чем получаемый по схеме Эйлера.
Пример. Решить уравнение d y /d x = – y, y (0) = 1 методом Рунге-Кутты.
Поскольку правая часть дифференциального уравнения имеет вид: f (x, y) = – y, схема метода при α = 0.5 представляется следующим образом:



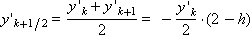

Построим последовательность значений искомой функции:




…

Pезультаты получаемого численного решения для значения аргумента x = 10 при различных шагах интегрирования приведены в табл. 15.1. Три верные значащие цифры получены для шага h = 0.01.
| Таблица 15.1. Результаты численного решения yn методом Рунге-Кутты второго порядка дифференциального уравнения y ' = – y с начальным условием y (0) = 1 | |||||||||||||||||||||
|
Оценим погрешность аппроксимации уравнения (1) разностной схемой метода Рунге-Кутты. Подставляем точное решение в разностный аналог исходного дифференциального уравнения и вычисляем невязку:
|
|
|

Подставим разложения функций


в полученное выражение:

Учитывая уравнение (1), а также выражение для производной

окончательно получаем, что ψ k = Ο (h 2), то есть метод Рунге-Кутты, независимо от значения параметра α, имеет второй порядок аппроксимации.
|
|
|