Формальная математическая запись
Приведем ниже вариант формальной математической записи для случая открытой системы тел со слабым нагревателем.
| dX1(t)/dt = K21 · (X2(t) – X1(t)) + K31 · (X3(t) – X1(t)) dX2(t)/dt = K12 · (X1(t) – X2(t)) + K32 · (X3(t) – X2(t)) + K42 · (X4(t) – X2(t)) + K52 · (X5(t) – X2(t)) dX3(t)/dt = 0 dX4(t)/dt = 0 dX5(t)/dt = (K · U(t) – X5(t))/L + K25 · (X2(t) – X5(t)) X1(0) = a X2(0) = b X3(0) = c X4(0) = d X5(0) = h U(t) = f(t) K12 = 0.2; K21 = 0.2; K31 = 0.1; K32 = 0.05; K42 = 0.1; K52 = 0.4; K25 = 0.4; K = 1; L = 1 Tk = 4
| | |
При реализации на математической машине среды Stratum эта запись будет дополнена элементами (функциями) ввода и вывода информации и командами управления (например, «стоп»), а часть элементов будет спрятана (например, при задании начальных условий).
Иногда (когда это удобно) начальные условия могут быть помещены внутрь уравнений. Для этого в следующей записи мы воспользуемся дельта-функцией Дирака (см. лекцию 31).
| dX1(t)/dt = K21 · (X2(t) – X1(t)) + K31 · (X3(t) – X1(t)) + a · delta(t) dX2(t)/dt = K12 · (X1(t) – X2(t)) + K32 · (X3(t) – X2(t)) + K42 · (X4(t) – X2(t)) + K52 · (X5(t) – X2(t)) + b · delta(t) dX3(t)/dt = c · delta(t) dX4(t)/dt = d · delta(t) dX5(t)/dt = (K · U(t) – X5(t))/L + K25 · (X2(t) – X5(t)) + h · delta(t) U(t):= f(t) K12:= 0.2; K21:= 0.2; K31:= 0.1; K32:= 0.05; K42:= 0.1; K52:= 0.4; K25:= 0.4; K:= 1; L:= 1; Tk:= 4 t:= t + Δt osc2d(T, X1) stop(T > Tk)
| | |
Напомним, что osc2d(T, X 1) — функция, рисующая на экране точку с координатами T и X 1 для каждого момента времени. Выше данная функция приведена условно: в действительности надо использовать несколько функций для настройки окон, масштаба изображения, цвета, толщины, стиля линии и тому подобного. Подробно реализацию двухмерного осциллографа в среде «Stratum-2000» вы можете посмотреть в тексте имиджа OSCSpace2D.
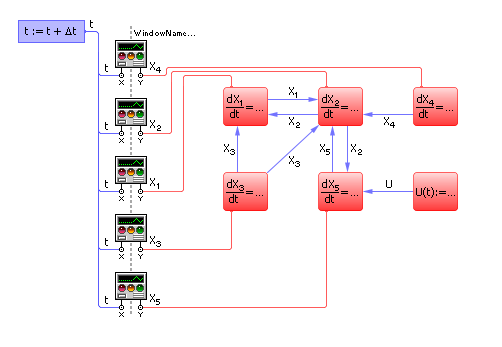
Приведенный выше вариант формальной математической записи подразумевает, что весь код заключен в рамках одного элемента (имиджа, если использовать термины среды «Stratum-2000»). Будет гораздо более наглядно, если распределить код по отдельным элементам, связав их между собой связями (см. рис. 11.9) — в этом случае структура проекта останется обозримой; кроме того, если потребуется изменить что-то в одном из блоков, то такой подход позволит не менять код в остальных блоках. Еще один плюс такого подхода — отдельные «кирпичики» схемы могут быть применены неоднократно в готовом виде в виде копии имиджа.
|
| Рис. 11.9. Схема проекта в среде Stratum-2000, реализующего полную модель теплопроводности системы тел с элементами интерфейса
|
Алгоритмическая реализация
В случае реализации на алгоритмической машине следует воспользоваться алфавитом алгоритмов: блоками начала и конца алгоритма, ввода-вывода информации, задания начальных условий, вычислительными блоками, блоками условия, конструкциями цикла. На рис. 11.10 представлена блок-схема алгоритма, имитирующего теплообмен между телами.
|
| Рис. 11.10. Блок-схема алгоритма, имитирующего теплообмен между телами
|
Заметьте, что для реализации нам понадобились следующие инструменты:
- устройства ввода информации (для задания параметров модели, параметров метода расчета, задания начальных условий процесса);
- устройство вывода информации;
- вычислительные блоки для реализации математических формул;
- цикл для имитации течения времени.
В теле цикла присутствуют:
- счетчик времени;
- условие выхода из цикла для контроля за временем моделирования;
- блок задания внешних воздействий;
- блок расчета приращений;
- блок расчета нового состояния системы;
- блок вывода текущих состояний.
В той или иной мере вышеназванные блоки обязательно присутствуют в каждом алгоритме данного типа.