 |
1. Классификация и механизм возникновения
|
|
|
|
Задание
1. Запустить программу расчета, ввести характеристики заданного преподавателем обрабатываемого материала (HD = HB·1, 5; Е; m), параметры режима УЗО (A, f, D), выполнить расчет пять раз для значений углов Q0, равных –60°, –30°, 0°, 30°, 60°, сохраняя результаты расчета в файле под своим именем.
2. Запустить файловую оболочку « Volcov Comander », найти файл с полученными результатами и вызвать его на просмотр (клавиша F3).
3. Открыть файл «grafics. xls» из программы MS Excel, ввести в таблицы полученные расчетные значения, построить графики
hmax = f (Fct), Fmax = f (Fct), dotp = f (Fct); для режима с максимальным значением hmax – графики F = f(t) и h(t) = f(t).
4. Рассчитать предельные значения величины упрочненного слоя при Fct min и при Fct max.
5. Рассчитать предельные значения параметра шероховатости поверхности при Fct min и при Fct max.
6. Сделать выводы по полученным результатам.
Содержание отчета
1. Краткая характеристика технологии обработки.
2. Описание модели и алгоритма расчета.
3. Входные данные.
4. Результаты расчета.
5. Графики.
6. Оценочные расчеты предельных параметров.
7. Выводы.
Контрольные вопросы
1. В чем заключается ультразвуковая обработка по схеме УЗО?
2. Где применяется модель УЗО, ее достоинства.
3. Что составляет основу модели УЗО?
4. Что является входными данными модели?
5. Что является выходными данными модели?
6. В чем заключаются особенности определения Fct в модели УЗО?
7. Какие характеристики поверхностного слоя можно оценить с помощью модели?
Лабораторная работа № 2
МОДЕЛИРОВАНИЕ напряженно-деформированного состояния деталей
при ультразвуковом поверхностном пластическом деформировании
Цель работы: познакомиться с работой модели напряженно-деформированного состояния при ультразвуковом пластическом деформировании по схеме УЗО, исследовать напряженные состояния деталей различных размеров после УЗО, проанализировать резуль-таты.
|
|
|
Долговечность деталей, работающих в условиях знакопеременного нагружения, усталостного износа, высоких динамических усилий, во многом определяется благоприятным распределением остаточных напряжений.
Остаточные напряжения возникают в деталях в большинстве технологических операций и по своей величине могут превышать напряжения, создаваемые внешними нагрузками в условиях эксплуатации. Релаксация остаточных напряжений может вызывать коробления деталей, негативно влияющие на точность формы и расположение их поверхностей.
1. Классификация и механизм возникновения
остаточных напряжений при ультразвуковом
пластическом деформировании
Образование остаточных напряжений связано в основном с неоднородным распределением деформаций по объему детали. При обработке деталей методами поверхностного пластического деформирования (ППД) возникновение остаточных напряжений обусловлено деформацией поверхностных слоев материала.
По классификации Н. Н. Давиденкова, остаточные напряжения делятся на напряжения первого, второго и третьего рода. Напряжения первого рода (макронапряжения) уравновешиваются в объеме всего тела. Напряжения второго рода (микронапряжения) уравновешиваются в объеме отдельных зерен. Напряжения третьего рода (субмикронапряжения) локализуются в объеме кристаллической решетки и представляют собой статические искажения решетки, т. е. смещения атомов на доли ангстрема из узлов кристаллической решетки.
Основное влияние на механические свойства поверхностного слоя и выносливость деталей оказывают остаточные напряжения первого рода. Поэтому в дальнейшем будем рассматривать только их.
|
|
|
При ультразвуковом пластическом деформировании образование остаточных напряжений и деформаций происходит в результате прохождения элементарного объема материала через очаг деформации, создаваемый упругопластическим контактом рабочей части инструмента с поверхностью детали (см. рис. 2, 4, 5 в лабораторной работе № 1).
Схематично процесс образования остаточных напряжений при УЗО представлен на рис. 9. Во время контакта элементарные объемы материала, попадающие в очаг деформации, испытывают напряжения, превышающие предел текучести, приводящие к упругопластической деформации материала, пластическая составляющая которой остается после снятия нагрузки. В то же время в элементарных объемах материала, лежащих ниже очага деформации, возникают напряжения, не превышающие предела текучести, создающие упругие деформации. После снятия нагрузки упругодеформированные объемы стремятся возвратиться в исходное положение, чему препятствуют пластическидеформированные объемы, бывшие в очаге деформации. В результате в последних возникают остаточные сжимающие напряжения.
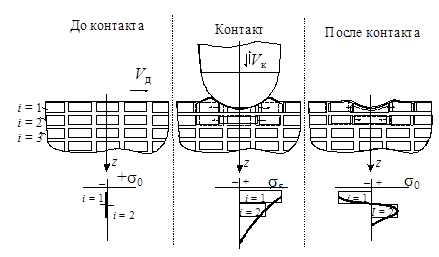
Рис. 9. Схема образования остаточных напряжений
в поверхностном слое при УЗО
2. Описание модели формирования напряженно-деформированного состояния при УЗО
Учитывая экспоненциальный характер изменения интенсивности деформации по глубине очага деформации, представим процесс УЗО схемой плоского изгиба прямого многослойного бруса (рис. 10). Воспользуемся допущением, что при изгибе продольные волокна не надавливают друг на друга, тогда можно считать, что слои испытывают простое растяжение (сжатие) и подчиняются закону Гука для линейного напряженного состояния. Для схемы на рис. 10 линейная деформация ez будет главной наибольшей деформацией, и в этом случае ее значение определяет интенсивность деформации в точке (ei =
= |e1| = |ez|). Наибольшее главное напряжение s1 при растяжении также направлено по линии действия растягивающей силы. В расчетных слоях на рис. 10 главные напряжения s1i направлены вдоль оси 0Z, и представляют собой нормальные напряжения szi, которые могут быть определены методом расчленения тела по формулам:
|
|
|
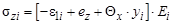 ; (4)
; (4)
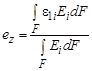 ;
; 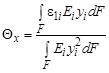 ,
,
где e1i – наибольшая главная деформация расчетного слоя (|e1i| = ei);
еz – относительная осевая деформация (еz < 0 если упрочненный слой лежит на вогнутой поверхности детали; еz > 0 если упрочненный слой лежит на выпуклой поверхности детали); Qx – относительный угол поворота поперечных сечений; yi – ордината центра расчетного слоя; Еi – модуль упругости материала слоя.
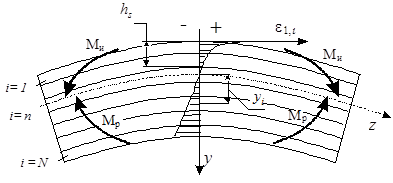
Рис. 10. Расчетная схема деформации при УЗО
В соответствии с методом расчлененного тела, деталь разбивается на расчетные слои таким образом, чтобы можно было принять в пределах каждого слоя деформации и напряжения постоянными на текущем этапе вычислений (см. рис. 10).
Применение стержневой аппроксимации позволяет поэтапно определять напряжения в расчетных слоях методом проб и итераций по формулам (4).
Расчеты в модели напряженно-деформированного состояния при УЗО проводятся по следующему алгоритму:
1. Определяется глубина очага деформации и максимальное значение интенсивности деформации для заданного режима УЗО.
2. Поперечное сечение детали разбивается по высоте на n слоев с площадью поперечного сечения i-го слоя, равной Fi.
3. Процесс внедрения деформатора на максимальную глубину разбивается по времени на 100 этапов, при этом принимаем, что значения глубины очага деформации и интенсивности деформации равномерно возрастают от 0 перед обработкой до максимальных значений на 100-м этапе.
4. Определяются деформации каждого слоя на текущем этапе расчета: в слоях, пересекающих очаг деформации – по экспоненциальному закону, в слоях за пределами очага деформации – по линейному закону из условия равновесия моментов внутренних сил.
5. Вычисляются изменения деформаций в каждом слое по сравнению с предыдущим (k – 1) этапом.
6. Предполагая, что все слои испытывают упругие деформации, определяются напряжения в каждом слое по формулам (4).
7. Определяются значения пределов текучести в каждом слое.
8. Вычисляются допустимые напряжения на k-м этапе:
|
|
|
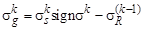 .
.
9. Определяется слой, в котором наиболее вероятно достижение пластической деформации по условию:
ni = | σ g i/ σ i |.
10. В слое, в котором наступила пластическая деформация, принимается: σ i = σ gi.
11. Пересчитываются напряжения в оставшихся слоях по форму-ле (4).
12. Определяется следующий слой, где возможна пластическая деформация (пункты 7–11). Итерационный процесс продолжается до тех пор, пока во всех слоях не будет выполнено условие ni ³ 1.
13. Определяются результирующие напряжения для k-го этапа: σ R(k) = σ R(k–1) + σ i(k).
Таким образом, входными данными расчета (рис. 11) являются механические свойства обрабатываемого материала (предел текучести, модуль нормальной упругости), толщина детали (S), число расчетных слоев (N), параметры очага деформации (глубина очага деформации (hs), максимальная интенсивность деформации (ε i, 0)).
Выходными данными расчета (рис. 11) являются распределение результирующих напряжений (σ zRi) и деформаций (Di) по слоям после ультразвукового деформирования, а также значение относительной осевой остаточной деформации (ez) детали в целом.
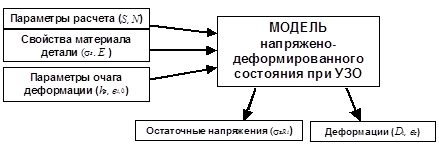
Рис. 11. Входные и выходные данные модели напряженно-
деформированного состояния при УЗО
|
|
|


