 |
2. Описание математической модели
|
|
|
|
2. Описание математической модели
Деформации и напряжения для полей температур могут быть определены методом расчленения тела, предложенным В. В. Абрамовым для стальных деталей. Этот метод позволяет решать задачи сложного напряженно-деформированного состояния, характерного для поверхностного упрочнения, при этом используется сравнительно простой математический аппарат упругопластического расчета методами сопротивления материалов. Так, расчет деформаций и напряжений, возникающих в реальных деталях при их нагреве и охлаждении, может быть сведен к расчету эквивалентной стержневой системы. При этом обеспечивается достаточная для технологических расчетов точность.
В соответствии с методом расчлененного тела, деталь разбивается на расчетные слои таким образом, чтобы можно было принять в пределах каждого слоя температуру, деформации и напряжения постоянными на текущем этапе вычислений (рис. 16).
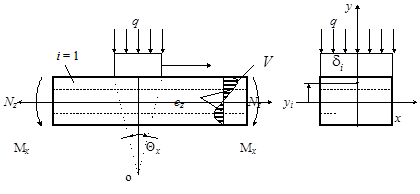Рис. 16. Расчетная схема для определения деформаций и напряжений
при поверхностном нагреве
Применение стержневой аппроксимации позволяет поэтапно определять напряжения в расчетных слоях методом проб и итераций по формуле:
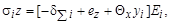(6)
где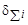 
= 
+ 
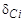– суммарная деформация расчетного слоя, равная сумме температурных и структурных деформаций; Еi – модуль упругости материала слоя при текущей температуре; еz – относительная осевая деформация (еz < 0, если упрочненный слой лежит на вогнутой поверхности детали, еz > 0 – в противном случае); Qx – относительный угол поворота поперечных сечений; yi – ордината центра расчетного слоя.
Расчеты в модели напряженно-деформированного состояния при поверхностном термоупрочнении проводится по следующему алгоритму.
|
|
|
1. Поперечное сечение детали разбивается по высоте на n слоев с площадью поперечного сечения i-го слоя, равной Fi.
2. Определяются температуры в каждом из расчетных слоев и суммарные температурные и структурные деформации каждого слоя при текущем значении температуры.
3. Вычисляются изменения деформаций в каждом слое по сравнению с предыдущим (k – 1) этапом.
4. Предполагая, что все слои испытывают упругие деформации, можно определить напряжения в каждом слое по формуле (6).
5. Определяются значения пределов текучести.
6. Вычисляются допустимые напряжения на k-м этапе:
.
7. Определяется слой, в котором наиболее вероятно достижение пластической деформации по условию:
ni = | 
gi / i|.
8. В слое, где наступила пластическая деформация, принимается i = gi.
9. Пересчитываются напряжения в оставшихся слоях по фор-
муле (6).
10. Определяется следующий слой, где возможна пластическая деформация (пункты 7–9). Итерационный процесс продолжается до тех пор, пока во всех слоях не будет выполнено условие ni > = 1.
11. Определяются результирующие напряжения для k–го этапа:
Таким образом, входными данными (рис. 17) расчета являются температурное поле [T(x, y) и шаг временной сетки (St)], создаваемое в детали при поверхностной закалке и механические свойства обрабатываемого материала (предел текучести ( s), модуль упругости (E)).
Выходными данными расчета (рис. 17) являются распределение результирующих напряжений ( zRi) и деформаций (Di) по слоям после поверхностного термоупрочнения, а также значение относительной осевой остаточной деформации (ez) детали в целом. Напряжения и деформации, соответствующие последнему (999) этапу расчета, являются остаточными, они сохраняются после обработки.
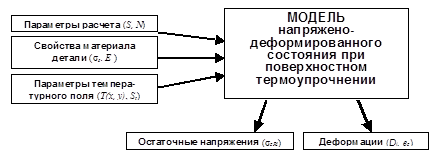
Рис. 17. Входные и выходные данные модели напряженно-деформированного
|
|
|
состояния при поверхностном термоупрочнении
Задание
1. Скопировать температурное поле, полученное в лабораторной работе № 3, из файла TEST. REZ в файл POLE. DAT.
2. Запустить программу расчета, выбрать вариант расчета № 7 (ввод поля из файла), ввести толщину образца, шаг временной сетки (0, 15 с), предел текучести и модуль упругости материала.
3. Рассчитать изменение температур, деформаций, результирующих напряжений в расчетных слоях № 1 и № 5 детали и остаточную осевую деформацию (еz) по этапам расчета k, сохраняя результаты в файл.
4. Открыть файл «grafics_4. xls» из программы MS Excel, ввести в таблицы полученные расчетные значения, построить T = f (k, i);
D = f (k, i); R = f (k, i); ez = f (k), где k – номер этапа; i – номер расчетного слоя, сохранить файл под новым именем.
5. Сделать выводы о конечном состоянии детали после поверхностного термоупрочнения.
|
|
|
