Начала математического анализа

Л.В. ЛИМАНОВА,

Л.А. Муратова

Высшая математика

В примерах и задачах

(для заочного факультета)

 

Самара

Самарский государственный технический университет

 

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

 

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

 

К а ф е д р а «Высшая математика и прикладная информатика»

 

 

Л.В. ЛИМАНОВА, Л.А. Муратова

 

 

Высшая математика

В примерах и задачах

(для заочного факультета)

 

 

Самара

Самарский государственный технический университет

Печатается по решению редакционно-издательского совета СамГТУ

 

УДК 517.531, 519.2

Л 58

 

Лиманова Л.В.

Л 58 Высшая математика в примерах и задачах (для заочного факультета): Учеб. пособ. по специальным разделам высшей математики / Л.В. Лиманова, Л.А. Муратова. – Самара: Самар. гос. техн. ун-т, 2010. – 86 с: ил.11.

 

Представлены типовые задачи с подробными решениями из следующих разделов курса высшей математики: «Линейная алгебра и аналитическая геометрия», «Дифференциальное исчисление», «Интегральное исчисление», «Ряды», «Дифференциальные уравнения», «Теория функций комплексной переменной», «Операционное исчисление», «Теория вероятностей». Пособие содержит тренировочные задания и может быть использовано при подготовке к контрольным работам и экзаменам по высшей математике.

Предназначено для студентов заочного факультета СамГТУ.

 

 

 

Рецензент канд. физ.-мат. наук, доц. Павлова Г.А.

 

 

УДК 517.531, 519.2

Л 58

 

© Л.В. Лиманова, Л.А. Муратова, 2010

© Самарский государственный

технический университет, 2010

 

 

Пособие содержит три главы, соответствующие трем семестрам курса высшей математики, изучаемой на заочном факультете СамГТУ.

В соответствии с программой здесь представлены следующие разделы: линейная алгебра, аналитическая геометрия, дифференциальное и интегральное исчисления, ряды, дифференциальные уравнения, теория функций комплексной переменной, операционное исчисление, теория вероятностей.

Работа состоит из набора типовых задач из указанных разделов с подробными решениями и необходимым теоретическим материалом. Кроме того, в приложении представлены тренировочные тесты с ответами для самоконтроля знаний.

Материал данной работы рекомендуется использовать для подготовки к контрольным работам и экзаменам по высшей математике на заочном факультете.

 

 

ГЛАВА 1

ЛИНЕЙНАЯ АЛГЕБРА,

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ,

НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА

Рассматриваются задачи по темам: теория определителей, действия с матрицами, решение систем линейных уравнений методом Гаусса.

ЛИНЕЙНАЯ АЛГЕБРА

 

Задача 1. Вычислить определитель .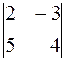

Решение. Определитель второго порядка 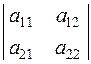равен разности между произведениями элементов главной диагонали ( и ) и побочной ( и ), то есть

.

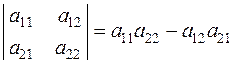Поэтому .

 

Задача 2. Вычислить определитель .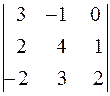

Решение. Рассмотрим два способа вычисления определителя третьего порядка.

Способ первый: используем формулу

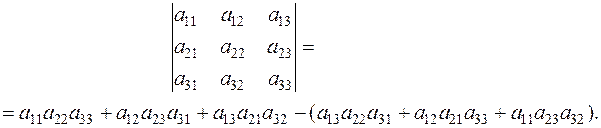
При этом полезна следующая схема. Первые три слагаемых – это произведения элементов, попавших на главную диагональ и в вершины двух треугольников (рис.1). Три слагаемых в скобках – это произведения элементов, попавших на побочную диагональ и в вершины двух других треугольников (рис.2).

 

 

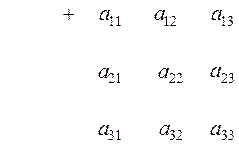
Рис. 1 Рис. 2

Получаем

.

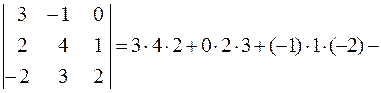
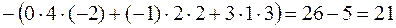Способ второй – разложение определителя по элементам строки или столбца. Например, для любой строки i имеет место формула:

 

Здесь 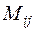- минор элемента 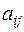- определитель второго порядка, получающийся в результате вычеркивания i -той строки и j -того столбца (то есть строки и столбца, на пересечении которых стоит элемент 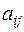). Аналогичная формула справедлива и для любого столбца.

Раскладывая заданный определитель по элементам первой строки, получим

 

 

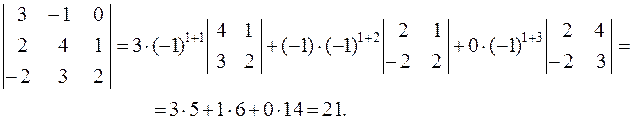
Задача 3. Умножить матрицу 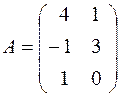на матрицу 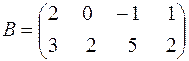и найти сумму элементов третьей строки результирующей матрицы.

Решение. Известно, что матрицу A размера (m − число строк, n − число столбцов) можно умножить на матрицу B размера 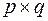, если n = p, причем в результате получится матрица 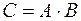размера :

 

 

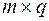Элемент c_ij (расположен на пересечении i- й строки и j -го столбца) результирующей матрицы C вычисляется по формуле

,

то есть равен сумме произведений элементов строки i матрицы A на соответствующие элементы столбца j матрицы B.

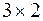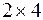В данной задаче матрицы A и B имеют размер и соответственно, и, значит, перемножаемы (n=p= 2), а результирующая матрица C будет иметь размер .

Найдем c ₁₁, для чего умножим поэлементно первую строку матрицы A на первый столбец матрицы B и результаты сложим:

.

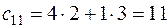Вычислим c ₁₂, умножив первую строку матрицы A на второй столбец матрицы B и сложив результаты:

.

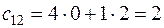Аналогично, находим остальные элементы

, ,

, ,

, ,

, ,

, .

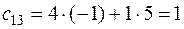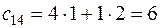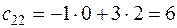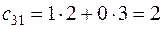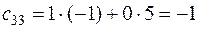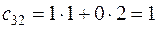Итак,

.

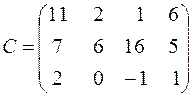При этом сумма элементов третьей строки матрицы C равна

.

 

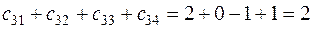Задача 4. Решить систему уравнений, приняв в качестве базисных переменных y и z:

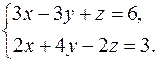
Решение. Решаем систему методом Гаусса. Запишем расширенную матрицу системы – матрицу из коэффициентов при неизвестных и свободных членов

~

Среди коэффициентов при неизвестных в первом уравнении есть удобная для дальнейших вычислений 1, ей соответствует переменная z. Назовем z базисной переменной. Исключим базисную переменную z из 2-го уравнения, для чего умножим 1-е уравнение на 2 и сложим со вторым. Получим эквивалентную исходной систему уравнений с матрицей

~

Учитывая тот факт, что в каждом уравнении выбирается одна базисная единица и по условию задачи другой базисной переменной должен быть y, получим базисную единицу во втором уравнении, разделив его на (-2):

~

Исключим у из первого уравнения. Для этого умножим второе уравнение на 3 и сложим с первым:

.

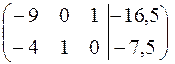Запишем систему уравнений, соответствующую последней матрице

Выразив базисные переменные у и z через свободную переменную х, получим общее решение системы уравнений

 

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

 

Рассматриваются задачи по темам: скалярное, векторное и смешанное произведения, уравнения прямой и плоскости.

 

Задача 5. Найти длину вектора .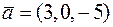

Решение. Длину вектора , или его модуль можно вычислить по формуле

.

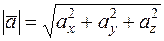Имеем .

 

Задача 6. Векторы и образуют угол . Зная, что 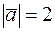, , найти скалярное произведение векторов .

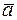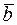Решение. Согласно определению скалярное произведение векторов и равно

.

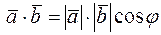Поэтому получим

.

 

Задача 7. Векторы 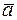и 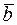образуют угол 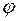. Известно, что 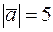, , а скалярное произведение векторов 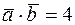. Найти .

Решение. Выразим из формулы скалярного произведения (см. задачу 6)

.

 

Задача 8. Вычислить скалярное произведение векторов и .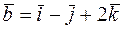

Решение. Используем формулу скалярного произведения векторов 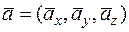и , согласно которой

.

Так как 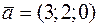, , 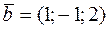то

.

 

Задача 9. Вычислить скалярное произведение 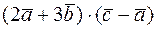, если известно, что , , .

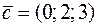Решение. Найдем векторы 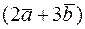и :

,

.

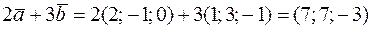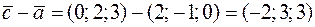Согласно формуле скалярного произведения (см. задачу 8) получим

.

 

Задача 10. Найти , при котором ортогональны векторы и .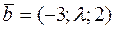

Решение. Условием ортогональности векторов 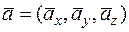и является равенство нулю их скалярного произведения

.

Имеем ,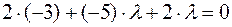

или , откуда .

 

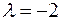Задача 11. Найти векторное произведение векторов .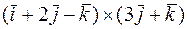

Решение. Вычисляем векторное произведение векторов 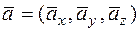и 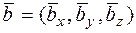по формуле

.

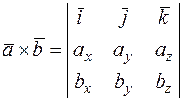Получаем

.

 

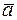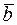Задача 12. Векторы и образуют угол . Зная, что 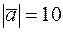, , 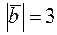найти модуль векторного произведения векторов .

Решение. В соответствии с определением векторного произведения имеет место формула

.

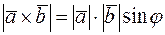Подставляя исходные данные, получим

.

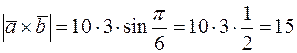Задача 13. Известно, что 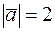, 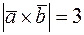и векторы 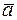и 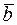образуют угол 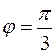. Найти .

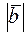Решение. Используя формулу модуля векторного произведения (см. задачу 12), найдем

.

С учетом исходных данных получим

.

Задача 14. Даны три вектора 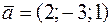, , 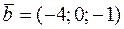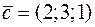. Найти:

1) смешанное произведение векторов ;

2) объем параллелепипеда, построенного на векторах , , ;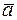

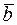3) объем треугольной пирамиды, построенной на векторах , , .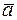

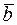Решение. 1) Смешанное произведение векторов 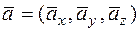, , 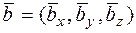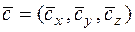вычисляется по формуле

.

Поэтому получаем

.

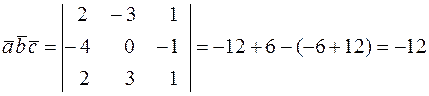2) Объем параллелепипеда, построенного на векторах 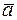, , 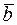, выражается через смешанное произведение и равен

.

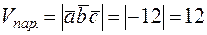3) Объем треугольной пирамиды, построенной на векторах 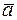, , 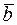, составляет 1/6 объема параллелепипеда, построенного на тех же векторах (рис.3), т.е.

.

 

Задача 15. Определить , при котором компланарны векторы , , .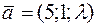

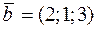Решение. Векторы называются компланарными, если они параллельны одной плоскости. Условием компланарности трех векторов является равенство нулю их смешанного произведения:

.

Приравнивая к нулю смешанное произведение векторов (см. задачу 14), получим уравнение для определения

.

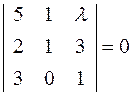Отсюда 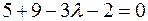, значит .

 

Задача 16. Составить уравнение плоскости, проходящей через три заданные точки А (1; 1; 1), В (1; 2; 3), С (2; 1; −1).

Решение. Воспользуемся уравнением плоскости, проходящей через три точки :

.

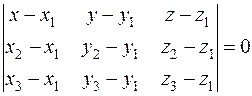Получим

,

,

,

,

.

 

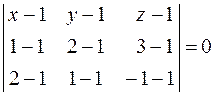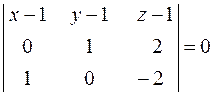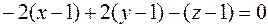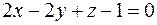Задача 17. Составить уравнение плоскости, проходящей через точку М (4; −1; 0) перпендикулярно вектору .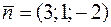

Решение. Уравнение плоскости, проходящей через точку 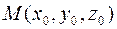перпендикулярно вектору 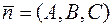имеет вид

.

Подставив заданные значения, получим

, или

.

 

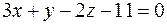Задача 18. Составить уравнение плоскости, проходящей через точку М (2; 0; −3) параллельно плоскости .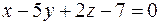

Решение. В уравнении плоскости вида

,

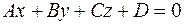где − координаты нормального вектора 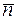– вектора, перпендикулярного к плоскости.

Таким образом, плоскость 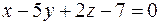имеет нормаль .

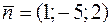Поскольку эта плоскость параллельна искомой, вектор 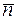будет нормалью и к искомой плоскости. Осталось воспользоваться уравнением плоскости, проходящей через данную точку перпендикулярно данному вектору (см. задачу 17). Получим

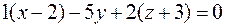, или

.

 

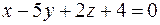Задача 19. Найти А и В, при которых плоскость 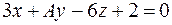параллельна плоскости .

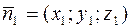Решение. Нормальные векторы заданных плоскостей (см. задачу 18) соответственно равны и . Так как плоскости параллельны, их нормали коллинеарны, а условием коллинеарности векторов и 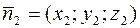является пропорциональность их координат:

.

Поэтому получим

.

Отсюда следует, что А = 7,5, В = −4.

 

Задача 20. Составить канонические и параметрические уравнения прямой, проходящей через точку М (−2; 7; 0) параллельно вектору .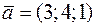

Решение. Канонические уравнения прямой, проходящей через точку 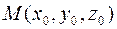параллельно вектору , имеют вид

.

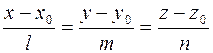Параметрические уравнения прямой можно получить, приравняв эти отношения к t

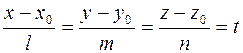
и выразив х, y и z через t:

.

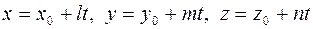Заметим, что вектор 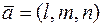называют направляющим вектором прямой.

С учетом исходных данных задачи получаем канонические уравнения

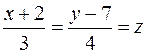
и параметрические уравнения искомой прямой

.

 

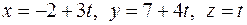Задача 21. Составить уравнения прямой, проходящей через точку М (4; 1; 5) параллельно прямой .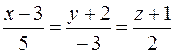

Решение. Прямая 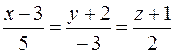параллельна своему направляющему вектору 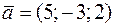. Но тогда вектор 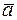параллелен и искомой прямой. Воспользовавшись уравнением прямой, проходящей через данную точку параллельно данному вектору (см. задачу 20), получим

.

 

Задача 22. Найти А и В, при которых параллельны прямые и .

Решение. Если прямые параллельны, то их направляющие векторы 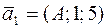и 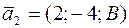коллинеарны, значит, координаты направляющих векторов пропорциональны (см. задачу 19):

.

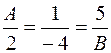Отсюда следует, что А = −0,5, В = −20.

 

Задача 23. Определить , при котором перпендикулярны две прямые 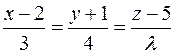и .

Решение. Так как прямые перпендикулярны, их направляющие векторы 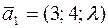и также перпендикулярны, но тогда скалярное произведение этих векторов равно нулю (см. задачу 10)

,

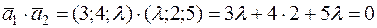откуда .

 

Задача 24. Составить уравнение прямой, проходящей через две точки М ₁(2; −5; 1) и М ₂(3; 4; −2).

Решение. Воспользуемся уравнением прямой, проходящей через две заданные точк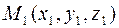и и :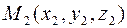

.

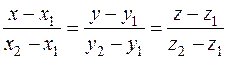Получим

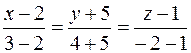, или

.

 

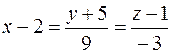Задача 25. Составить уравнение плоскости, проходящей через точку М (1; −3; 0) перпендикулярно прямой .

Решение. Так как прямая перпендикулярна плоскости, направляющий вектор этой прямой также перпендикулярен плоскости.

Согласно уравнению плоскости, проходящей через точку М перпендикулярно вектору 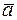(см. задачу 17), получим

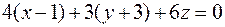, или

.

Задача 26. Составить уравнение прямой, проходящей через точку М (2; 7; −1) перпендикулярно плоскости .

Решение. Так как прямая перпендикулярна плоскости, нормальный вектор этой плоскости параллелен прямой. В соответствии с уравнением прямой, проходящей через точку М параллельно данному вектору 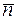(см. задачу 20), имеем

.

 

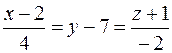НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА

 

Рассматриваются следующие задачи: вычисление пределов, дифференцирование функций одной и нескольких переменных, приложения дифференциального исчисления к исследованию функций.

 

Задача 27. Вычислить .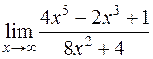

Решение. При 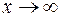числитель и знаменатель дроби неограниченно возрастают. В этом случае говорят, что имеет место неопределенность 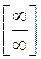. Выносим за скобки в числителе и знаменателе переменную в старшей степени и после сокращения получаем:

.

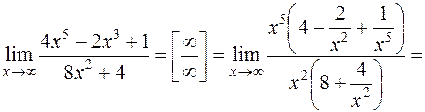
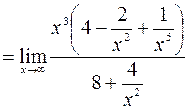При величины , , 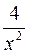стремятся к 0, 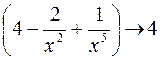, весь числитель стремится к 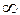, а знаменатель . Поэтому вся дробь стремится к .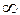

Таким образом,

 

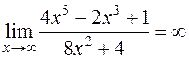
Задача 28. Вычислить .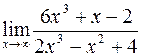

Решение. При числитель и знаменатель стремятся к . Это неопределенность вида 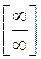. Раскрываем ее (см. задачу 27):

.

 

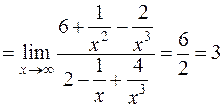Задача 29. Вычислить .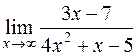

Решение. Поскольку числитель и знаменатель при 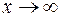стремятся к 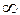, имеем неопределенность 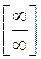. Раскрываем ее (см. задачу 27):

.

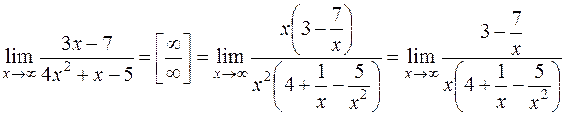Так как при 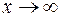числитель стремится к 3, а знаменатель − к 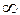, то вся дробь стремится к 0 и

.

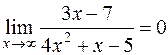Замечание. Полученные в задачах 27-29 результаты можно обобщить следующим образом:

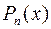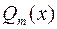Здесь и - многочлены степеней n и m соответственно, причем

, .

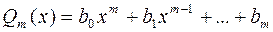Это правило позволяет сразу получить результат, минуя вычисления, одним лишь сравнением старших степеней многочленов числителя и знаменателя (в задаче 27: 5>2, значит, предел равен ; в задаче 28: 3 = 3, значит, предел равен ; в задаче 29: 1 < 2, значит, предел равен 0).

 

Задача 30. Вычислить .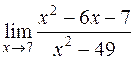

Решение. При 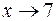числитель и знаменатель дроби стремятся к 0. Это неопределенность вида 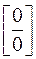. Разложив числитель и знаменатель на множители и выполнив сокращение на множитель (х − 7) (из-за которого и возникла неопределенность), получим

.

 

Задача 31. Вычислить .

Решение. Так как при 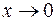выражение 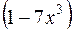стремится к 1, а показатель степени 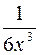− к бесконечности, имеем неопределенность 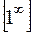. Раскрываем ее с помощью второго замечательного предела

.

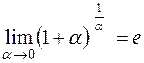Считая 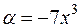, достраиваем выражение до второго замечательного предела и получаем

.

 

Задача 32. Вычислить .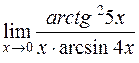

Решение. Поскольку при числитель и знаменатель дроби стремятся к 0, имеем неопределенность 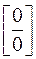. Воспользовавшись формулами таблицы эквивалентности [приложение 4] для бесконечно малой величины ():

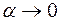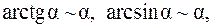
получим при :

Заменяя числитель и знаменатель на эквивалентные бесконечно малые величины, найдем

.

 

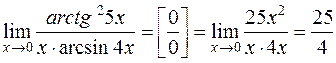Задача 33. Вычислить .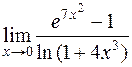

Решение. Имеем неопределенность 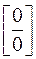. Согласно формулам таблицы эквивалентности [приложение 4] для бесконечно малой величины ()

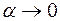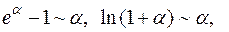
поэтому при : .

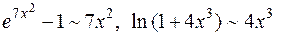Тогда

.

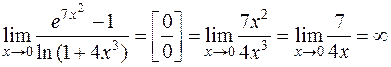Задача 34. Найти 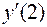, если .

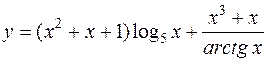Решение. Применяя формулы дифференцирования произведения и частного [приложение 4]:

,

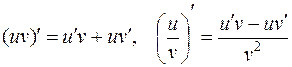имеем

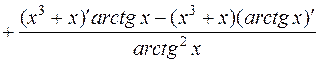
и далее, с учетом формул дифференцирования элементарных функций (2),(5), (13) [приложение 4]

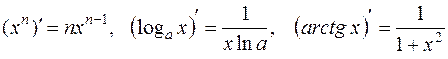
получим

.

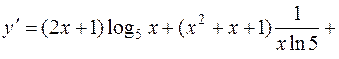
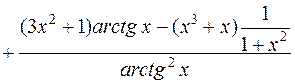Подставим в производную х = 2:

.

 

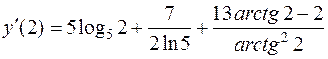Задача 35. Для функци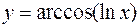и найти .

Решение. Применим правило дифференцирования сложной функции: если , , то .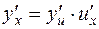

В данном случае 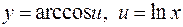. Согласно формулам (12), (6) [приложение 4]

.

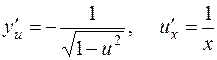Тогда

.

 

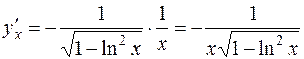Задача 36. Для функци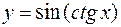и найти .

Решение. По правилу дифференцирования сложной функции , где , имеем .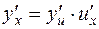

Так как , применяем формулы (7), (10) [приложение 4]:

.

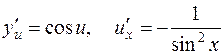Окончательно,

.

 

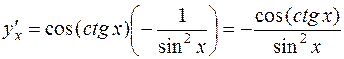Задача 37. Дана функция 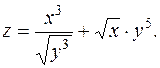Найти ее частные производные и 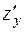в точке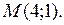

Решение. Преобразуем данную функцию к виду

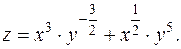
Вычислим частную производную 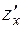, используя формулу дифференцирования (2) [приложение 4]

и считая у константой:

Подставив вместо х и у координаты точки 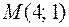, получим

Найдем 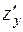, считая х константой:

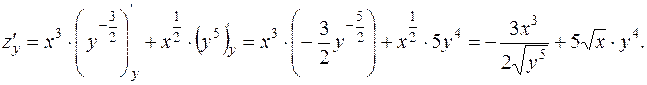
Подставляя координаты точки 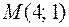, получим

 

Задача 38. Найти интервалы возрастания и убывания функции .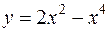

Решение. Функция y = f(x) возрастает, если 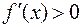, и убывает, если 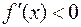. Найдем :

.

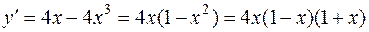Определим знаки первой производной и промежутки монотонности функции у

x		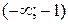−1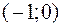
	+		−		+		−
y

Итак, функция возрастает на интервалах и убывает на интервалах .

 

Задача 39. Найти интервалы выпуклости и вогнутости функции