 |
Операционное исчисление, теория вероятностей»
|
|
|
|
| № | Задания | Варианты ответов | |||||||||||||
| 1. | Вычислить 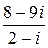
| 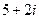
| 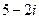
| 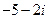
| 
| 
| |||||||||
| 2. | Представить в показательной форме число 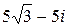
| 
| 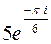
| 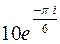
| 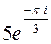
| 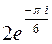
| |||||||||
| 3. | Вычислить 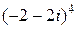
| 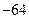
| 
| 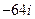
| 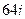
| 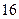
| |||||||||
| 4. | Решить уравнение 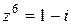
| 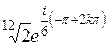 , , 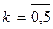
| 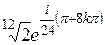 , ,
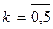
| 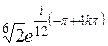 , ,
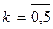
| 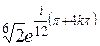 , ,
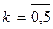
| 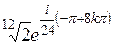 , ,
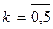
| |||||||||
| 5. | Вычислить 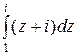
| 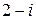
| 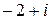
| 
| 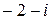
| 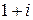
| |||||||||
| 6. | Найти изображение для оригинала 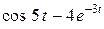
| 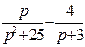
| 
| 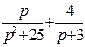
| 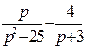
| 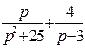
| |||||||||
| 7. | Найти изображение для оригинала 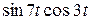
| 
| 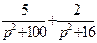
| 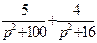
| 
| 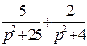
| |||||||||
| 8. | Найти изображение для оригинала 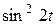
| 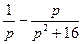
| 
| 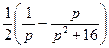
| 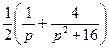
| 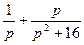
| |||||||||
| 9. | Найти оригинал для изображения 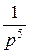
| 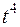
| 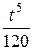
| 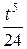
| 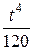
| 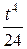
| |||||||||
| 10. | Найти оригинал для изображения 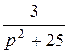
| 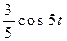
| 
| 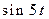
| 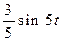
| 
| |||||||||
| 11. | Найти изображение свертки функции 
| 
| 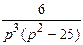
| 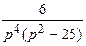
| 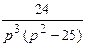
| 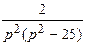
| |||||||||
| 12. | Решить дифференциальное уравнение

| 
| 
| 
| 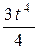
| 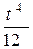
| |||||||||
| 13. | Устройство содержит 4 независимо работающих элемента с вероятностями отказа 0,9; 0,4; 0,2; 0,5. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент. | 0,976 | 0,024 | 0,964 | 0,97 | 0,98 | |||||||||
| 14. | Из 10 стрелков 5 попадают в цель с вероятностью 0,4; 2 – с вероятностью 0,8; 3 – с вероятностью 0,6. Найти вероятность того, что наудачу выбранный стрелок попадет в цель. | 0,48 | 0,18 | 0,54 | 0,64 | 0,72 | |||||||||
| 15. | Дискретная случайная величина Х задана законом распределения. Найти D(X), если М(Х) = 2,9.
| 18,9 | 2,89 | 0,89 | 1,09 | 1,89 | |||||||||
| 16. | Дискретная случайная величина задана рядом распределения. Найти D(X).
| 6,76 | 4,28 | 3,75 | 5,12 | 2,44 | |||||||||
| 17. | Дискретная случайная величина Х задана рядом распределения. Найти
| ||||||||||||||
| 18. | Задана плотность распределения непрерывной случайной
величины Х: 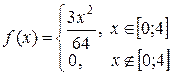 . Найти . Найти 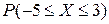 . .
| 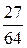
| 
| 
| 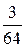
| 
| |||||||||
| 19. | Задана плотность распределения непрерывной случайной
величины Х: 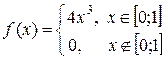 . Найти М (Х). . Найти М (Х).
| 
| 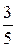
| 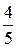
| |||||||||||
| 20. | Найти дисперсию случайной величины Х – числа появлений события А в 18 независимых испытаниях, если вероятности появления события в каждом испытании одинаковы, а М (Х) = 8. | 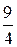
| 
| 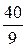
| 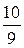
| 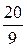
| |||||||||
| 21. | Случайная величина Х – число появлений события А в n испытаниях распределена по биномиальному закону с М (Х) = 10, D (X) = 7. Найти вероятность появления события А в каждом испытании. | 0,3 | 0,2 | 0,35 | 0,4 | 0,43 | |||||||||
| 22. | Детали, выпускаемые цехом, по размеру диаметра распределяются по нормальному закону с параметрами: М (Х) = 0,5 см, D (X) =0,36 см2. Деталь считается годной, если ее диаметр не менее 0,464 и не более 0,536 см. Определить, какой процент деталей будет забракован. | 4,78% | 95,22% | 97,61% | 2,39% | 90,27% | |||||||||
| 23. | Дальность полета снаряда распределена нормально с математическим ожиданием 800 м и средним квадратическим отклонением 40 м. Определить интервал, в который согласно правилу 3 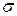 попадет снаряд с вероятностью 0,9973. попадет снаряд с вероятностью 0,9973.
| (720, 880) | (780, 820) | (760, 840) | (680, 920) | (640, 960) | |||||||||
|
|
|
Правильные ответы
| № задания | |||||||||||||||||||||||
| Ответ |
Приложение 4
Таблица эквивалентности бесконечно малых
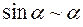
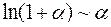
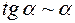
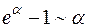


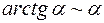

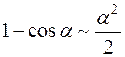 (формулы справедливы при
(формулы справедливы при 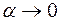 )
)
ТАБЛИЦА ПРОИЗВОДНЫХ
ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
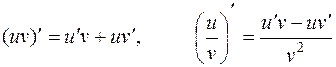
| 1. | 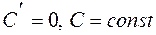
| 8. | 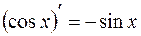
|
| 2. | 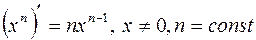
| 9. | 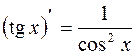
|
| 3. | 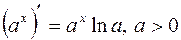
| 10. | 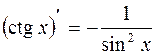
|
| 4. | 
| 11. | 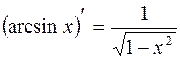
|
| 5. | 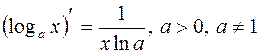
| 12. | 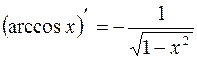
|
| 6. | 
| 13. | 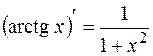
|
| 7. | 
| 14. | 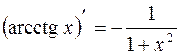
|
Приложение 5
ТАБЛИЦА интегралов
ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
| 1. | 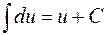
| 10. | 
|
| 2. | 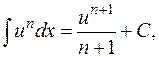 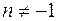
| 11. | 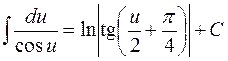
|
| 3. | 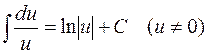
| 12. | 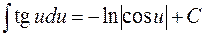
|
| 4. | 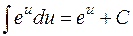
| 13. | 
|
| 5. | 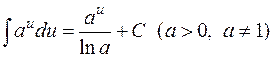
| 14. | 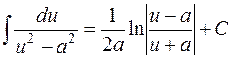
|
| 6. | 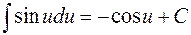
| 15. | 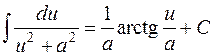
|
| 7. | 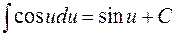
| 16. | 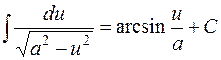
|
| 8. | 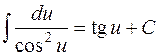
| 17. | 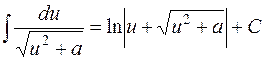
|
| 9. | 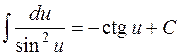
| ||
Формула интегрирования по частям: 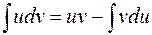 Формула Ньютона–Лейбница:
Формула Ньютона–Лейбница: 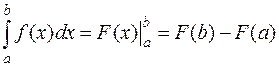
|
Некоторые тригонометрические формулы
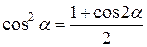 ;
; 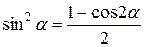 ;
; 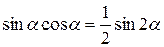 ;
;
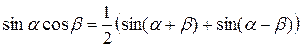 ;
;
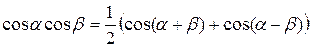 ;
;
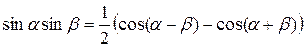 .
.
Ряды
Необходимый признак сходимости ряда: Если ряд 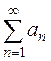 сходится, то
сходится, то 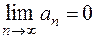 (если же
(если же 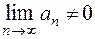 , то ряд расходится).
, то ряд расходится).
Радикальный признак Коши: Если для положительного ряда 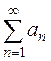 существует предел
существует предел  , то
, то
|
|
|
1) при b < 1 ряд сходится;
2) при b > 1 ряд расходится;
3) при b =1 рассматриваемый признак не дает ответа на вопрос о сходимости ряда.
Признак Даламбера: Если для положительного ряда 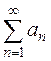 существует предел
существует предел 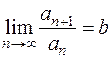 , то
, то
1) при b < 1 ряд сходится;
2) при b > 1 ряд расходится;
3) при b =1 рассматриваемый признак не дает ответа на вопрос о сходимости ряда.
Предельный признак сравнения: Если существует конечный и отличный от нуля предел 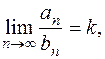 то положительные ряды
то положительные ряды 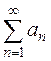 и
и 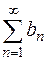 одинаковы в смысле сходимости.
одинаковы в смысле сходимости.
Обобщенный гармонический ряд 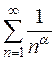
1) сходится при 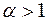 ;
;
2) расходится при 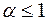 (здесь
(здесь  – действительное число).
– действительное число).
Признак Лейбница для знакочередующихся рядов: Ряд 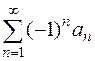 сходится, если выполняются два условия:
сходится, если выполняются два условия:
1) 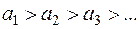 ; 2)
; 2) 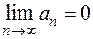 .
.
Радиус сходимости R степенного ряда 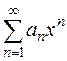
 ,
, 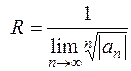 .
.
Дифференциальные уравнения
Линейное дифференциальное уравнение первого порядка
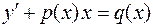
решается методом Бернулли с помощью подстановки
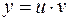 ,
, 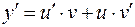 .
.
|
|
|



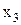 , если М (Х) = 1,7.
, если М (Х) = 1,7.