 |
Дифференциальные уравнения
|
|
|
|
Рассматриваются дифференциальные уравнения первого порядка (с разделяющимися переменными, однородные, линейные), однородные дифференциальные уравнения высших порядков с постоянными коэффициентами, задача Коши.
Задача 66. Найти общее решение дифференциального уравнения
.
Решение. Уравнение, содержащее переменную, функцию этой переменной, а также производные этой функции, называется дифференциальным. Решить дифференциальное уравнение – значит найти функцию у (х), обращающую уравнение в тождество.
В данном уравнении можно разделить переменные, то есть с помощью преобразований сделать так, чтобы в одной части было выражение, зависящее только от х, а в другой – только от у. Такие уравнения называются дифференциальными уравнениями с разделяющимися переменными.
Перепишем уравнение, используя другое обозначение для производной: 
. Получим
.
Разделим переменные, умножив уравнение на выражение 
. Это приведет к равенству
.
Проинтегрируем обе части полученного уравнения
,
вычислим интегралы с помощью формул интегрирования (4) и (2) [приложение 5]
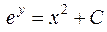
и выразим у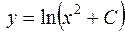 
.
Получившееся выражение называется общим решением дифференциального уравнения.
Задача 67. Найти общее решение дифференциального уравнения
.
Решение. Данное дифференциальное уравнение также относится к уравнениям с разделяющимися переменными и решается аналогично задаче 66. Перепишем уравнение в виде
.
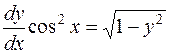Разделим переменные, умножив обе части уравнения на 
:
.
В результате вычисления интегралов
по формулам интегрирования (16) и (8) [приложение 5] получим
.
Тогда общее решение дифференциального уравнения будет иметь вид
.
Задача 68. Найти общее решение дифференциального уравнения
|
|
|
.
Решение. Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям первого порядка вида
.
Такое уравнение можно решать методом Бернулли с помощью подстановки
,
где u (x) и v (x) – две неизвестные функции. Подставляя в исходное уравнение
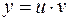и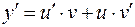 
,
получим
, или 
.
Так как одна из неизвестных функций может быть выбрана произвольно (поскольку лишь произведение uv должно удовлетворять исходному уравнению), возьмем в качестве v одно из частных решений уравнения
.
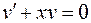При этом исходное дифференциальное уравнение примет вид
.
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные
,
, 
.
Интегрируя, находим
,
, или 
(формулы интегрирования (3), (2) [приложение 5]).
Взяв в качестве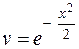 
, преобразуем уравнение 
:
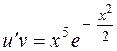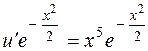, откуда 
.
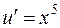Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и
, 
,
, 
(формулы интегрирования (1), (2) [приложение 5]).
Возвращаясь к функции у, получим общее решение исходного дифференциального уравнения
.
Задача 69. Найти общий интеграл дифференциального уравнения
Решение. Данное уравнение относится к однородным дифференциальным уравнениям первого порядка вида 
и решается заменой 
(здесь 
– новая функция), приводящей его к уравнению с разделяющимися переменными. Выполняя замену, получим
, 
Исходное уравнение примет вид
,
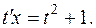
Разделяем переменные и интегрируем
, 
,
.
Согласно формулам интегрирования (15), (3) [приложение 5] имеем
,
Выполнив обратную замену, получаем решение исходного уравнения, записанное в неявном виде, то есть общий интеграл дифференциального уравнения
.
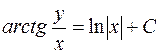Задача 70. Найти общее решение уравнения 
.
Решение. Данное дифференциальное уравнение относится к однородным линейным дифференциальным уравнениям второго порядка с постоянными коэффициентами
|
|
|
.
Этому уравнению соответствует так называемое характеристическое уравнение
,
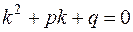от корней k 1 и k 2 которого зависит вид общего решения исходного дифференциального уравнения. При этом
1) если k 1и k 2– действительны и различны (дискриминант D > 0, 
), общее решение дифференциального уравнения имеет вид
,
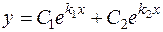то есть каждому корню 
соответствует слагаемое вида 
;
2) если k 1и k 2 –действительные и равные (дискриминант D = 0, k 1= k 2 = k), общее решение дифференциального уравнения имеет вид
, или 
;
3) если k 1и k 2 – комплексные (дискриминант D < 0,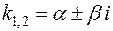 
) общее решение дифференциального уравнения в этом случае будет иметь вид
.
Составляя характеристическое уравнение для заданного дифференциального уравнения , получим
.
Оно имеет два различных действительных корня k 1= 1 и k 2 = 2 (случай 1). Поэтому общее решение будет записано в виде
.
Задача 71. Найти общее решение уравнения 
.
Решение. Согласно теории, изложенной в задаче 70, составим характеристическое уравнение
.
Оно имеет два равных корня k 1= k 2 = 3 (случай 2). Поэтому общее решение есть
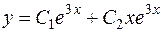, или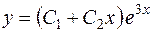 
.
Задача 72. Найти общее решение уравнения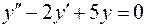 
.
Решение. Согласно теории, изложенной в задаче 70, составим характеристическое уравнение
.
Дискриминант этого уравнения отрицательный (случай 3)
.
Это означает, что уравнение имеет комплексные корни
,
где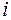 
– мнимая единица, такая, что 
.
Так как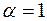 
, 
, общим решением будет
.
Задача 73. Найти общее решение уравнения 
.
Решение. Согласно теории, изложенной в задаче 70, составим характеристическое уравнение
,
откуда получаем: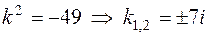 
(корни комплексные – случай 3). Здесь 
, 
, значит, общее решение имеет вид
.
Задача 74. Найти общее решение дифференциального уравнения
.
Решение. Данное уравнение является линейным однородным дифференциальным уравнением третьего порядка с постоянными коэффициентами и решается аналогично уравнениям второго порядка (см. задачу 70). Его характеристическое уравнение
, или
, откуда
.
Паре корней 
соответствует решение
Корню 
соответствует решение
.
Общее решение исходного уравнения есть сумма полученных решений
.
Задача 75. Найти частное решение дифференциального уравнения 
, удовлетворяющее условиям: 
, 
.
|
|
|
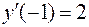Решение. Дифференциальное уравнение вида
решается n –кратным последовательным интегрированием:
,
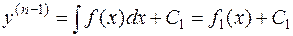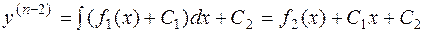и т.д.
В данном случае 
, поэтомуинтегрируем два раза. При этом получим (формула интегрирования (2) [приложение 5])
.
Подставив начальное условие 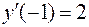, найдем константу С 1:
, 
.
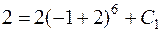Тогда уравнение примет вид
.
Еще раз проинтегрируем:
.
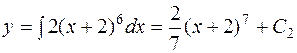Подставив начальное условие , найдем константу С 2:
, 
.
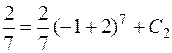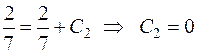Значит, частное решение исходного дифференциального уравнения имеет вид
.
Задача 76. Найти частное решение уравнения 
, удовлетворяющее условиям: 
, 
.
Решение. Данное дифференциальное уравнение решается аналогично задаче 75. Проинтегрировав первый раз, получим
(формула интегрирования (4) [приложение 5]).
Подставив начальное условие , найдем константу С 1
, 
.
Уравнение примет вид
.
Еще раз проинтегрируем, получим
.
Подставив начальное условие , найдем константу 
:
, 
.
Итак, частное решение дифференциального уравнения имеет вид
.
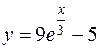ГЛАВА 3
|
|
|
