 |
Дифференциальные уравнения
|
|
|
|
Интегралы
Рассматриваются следующие задачи: вычисление неопределенного интеграла, определенного интеграла, вычисление площадей плоских фигур.
Задача 40. Вычислить интеграл 
.
Решение. Воспользуемся основными свойствами неопределенного интеграла (интеграл от суммы равен сумме интегралов, а постоянный множитель можно выносить за знак интеграла) и применим формулы (2), (3) и (1) из таблицы интегралов [приложение 5]:
.
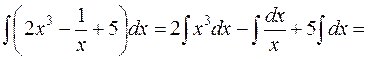
Задача 41. Вычислить интеграл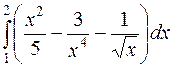 
.
Решение. Данный интеграл является определенным. Для его вычисления необходимо воспользоваться формулой Ньютона–Лейбница [приложение 5]
.
Тогда в соответствии с формулой (2) [приложение 5] имеем
.
Задача 42. Вычислить интеграл 
.
Решение. Интеграл можно свести к табличному (7) [приложение 5], если сделать замену переменной, приняв 3 х = t. Дифференцируя обе части равенства, получим
, или 
.
Так как интеграл определенный, необходимо также изменить пределы интегрирования. При этом получим
= 
.
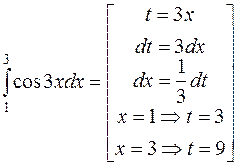Замечание. Задачу можно было решить, используя правило: если
, то 
.
В данном случае так как
, то 
,
Поэтому 
.
Задача 43. Вычислить интеграл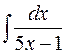 
.
Решение. Интеграл можно свести к табличному (3) [приложение 5], если выполнить замену: t = 5 х – 1. Тогда
.
Задача 44. Вычислить интеграл 
.
Решение. Интеграл можно свести к табличному (2) [приложение 5], если сделать замену переменной: t = 2 х + 7.
Но можно использовать замечание к задаче 42. В этом случае поскольку 
, имеем
.
Задача 45. Вычислить интеграл 
.
Решение. Интеграл можно свести к табличному (9) [приложение 5] с помощью замены t = х / 5:
.
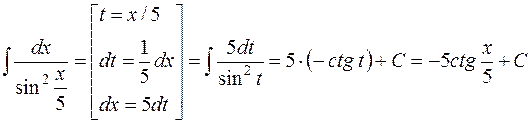Задача 46. Вычислить интеграл 
.
Решение. Интеграл можно свести к табличному (4) [приложение 5] заменой t = 6 х. Так как интеграл определенный, изменяем и пределы интегрирования:
|
|
|
= 
.
Задача 47. Вычислить интеграл 
.
Решение. Интеграл относится к группе интегралов: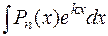 
, 
, 
, где Pn (x) – многочлен степени п. Вычисление таких интегралов выполняется интегрированием по частям [приложение 5]
Если за и принять многочлен Pn (x), то в результате применения формулы интегрирования по частям интеграл упростится (уменьшится степень многочлена).
Обозначим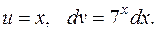 
Найдем 
:
(формула интегрирования (5) [приложение 5]). Тогда
.
Задача 48. Вычислить интеграл 
.
Решение. Этот интеграл относится к группе интегралов вида 
, 
, 
, 
(Pn (x) – многочлен степени п) и вычисляется по формуле интегрирования по частям [приложение 5].
В результате применения этой формулы исходный интеграл упростится, если за и принимать функции 
.
Итак, положим
Тогда
.
Получаем
.
Задача 49. Вычислить интеграл 
.
Решение. Для определенного интеграла также применима формула интегрирования по частям
Положим 
, 
(см. задачу 47). Тогда
и 
(формула интегрирования (6) [приложение 5]).
Итак,
.
Задача 50. Вычислить интеграл 
.
Решение. Это интеграл вида 
с чётными m и n (в данном случае 
) и вычисляется с помощью формул тригонометрии [приложение 5].
Воспользуемся формулой понижения степени [приложение 5]
,
получим
(формулы интегрирования (1), (7) [приложение 5]).
Задача 51. Вычислить 
.
Решение. Применяя тригонометрическую формулу [приложение 5]
,
получим
(формула интегрирования (6) [приложение 5]).
Задача 52. Вычислить площадь области D, ограниченной линиями 
, y = x – 1, x = 0, x = 2.
Решение. Площадь области D, ограниченной линиями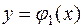 
, 
, x = а, x = b (рис. 4), вычисляется по формуле
.
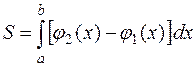Построим заданную область D (рис. 5). Слева область ограничена прямой 
, справа – прямой 
, снизу – прямой 
, сверху – параболой .
Подставляя все данные в формулу, найдем площадь области D:
|
|
|
(кв. ед.)
Задача 53. Вычислить площадь области D, ограниченной линиями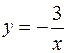 
, y = 0, x = 1, x = 3.
Решение. Построим заданную область D (рис. 6), ограниченную слева – прямой 
, справа – прямой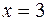 
, снизу – параболой 
, сверху – прямой 
.
Подставляя все данные в формулу площади (см. задачу 52), получим
(кв. ед.)
Ряды
Рассматриваются задачи о сходимости положительных, знакопеременных и функциональных рядов.
Задача 54. Исследовать на сходимость ряд 
.
Решение. Необходимый признак сходимости ряда гласит [приложение 5 – РЯДЫ]: Если ряд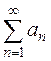 
сходится, то 
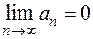(если же 
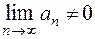, то ряд расходится).
Здесь 
. Рассмотрим предел
.
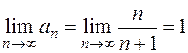Предел не равен нулю, следовательно, ряд расходится.
Задача 55. Исследовать на сходимость ряд 
.
Решение. Используем радикальный признак Коши [приложение 5 – РЯДЫ]: Если для положительного ряда 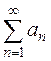существует предел
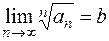, то
1) при b < 1 ряд сходится;
2) при b > 1 ряд расходится;
3) при b =1 рассматриваемый признак не дает ответа на вопрос о сходимости ряда.
Найдем предел
.
Найденный предел 
. Следовательно, данный ряд расходится.
Задача 56. Исследовать на сходимость ряд 
.
Решение. Используем признак Даламбера [приложение 5 – РЯДЫ]: Если для положительного ряда 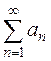существует предел
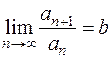, то
1) при b < 1 ряд сходится;
2) при b > 1 ряд расходится;
3) при b =1 рассматриваемый признак не дает ответа на вопрос о сходимости ряда.
Здесь 
, 
, тогда имеем
.
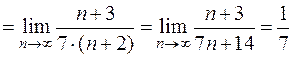Найденный предел 
. Следовательно, данный ряд сходится.
Задача 57. Исследовать на сходимость ряд 
.
Решение. Применяем признак Даламбера (см. задачу 56). Здесь 
, 
, поэтому
Найденный предел 
. Следовательно, ряд расходится.
Задача 58. Исследовать на сходимость ряд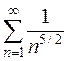 
.
Решение. Ряд 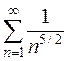– это обобщенный гармонический ряд вида 
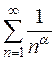, где 
– действительное число. Известно, что такой ряд [приложение 5 – РЯДЫ]
1) сходится при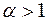 
;
2) расходится при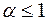 
.
Так как в исходном примере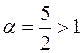 
, то ряд сходится.
Задача 59. Исследовать на сходимость ряд 
.
Решение. При исследовании сходимости ряда можно воспользоваться предельным признаком сравнения положительных рядов [приложение 5 – РЯДЫ]: Если существует конечный и отличный от нуля предел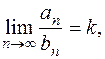 
то положительные ряды 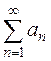и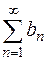 
одинаковы в смысле сходимости.
Для сравнения возьмем обобщенный гармонический ряд 
. Он сходится (см. задачу 58). Применяя предельный признак сравнения, получим
|
|
|
.
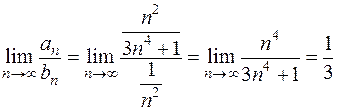Так как предел 
конечен и отличен от нуля, то ряд 
также сходится.
Задача 60. Исследовать на сходимость ряд 
.
Решение. Этот ряд относится к знакочередующимся рядам вида
,
где 
(n = 1, 2, 3…).
Cогласно признаку Лейбница [приложение 5 – РЯДЫ] такой ряд сходится, если выполняются два условия:
1) 
; 2) .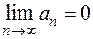
Для данного ряда имеем: 
.
Условия теоремы выполнены:
1) 
; 2) 
.
Следовательно, ряд сходится.
Рассматриваемый ряд является частным случаем знакопеременного (с произвольным чередованием знаков) ряда. Сходимость знакопеременного ряда может быть абсолютной или условной в зависимости от того, сходится или расходится соответствующий ряд из абсолютных величин членов знакопеременного ряда.
Пусть 
– знакопеременный ряд. Если сходится ряд 
, составленный из модулей, то ряд называется абсолютно сходящим ся. Может оказаться, что ряд расходится, а ряд сходится. В этом случае ряд называется условно сходящимся.
Итак, рассмотрим ряд, составленный из абсолютных величин членов данного ряда
= 
.
Он положительный. Исследуем его на сходимость по признаку Даламбера [приложение 5 – РЯДЫ].
Так как 
, получим
.
Тогда ряд 
сходится, следовательно, ряд 
сходится абсолютно.
Задача 61. Исследовать на сходимость ряд 
.
Решение. Для данного ряда выполняются условия признака Лейбница [приложение 5 – РЯДЫ]:
1) 
2) 
.
Значит, ряд сходится. Исследуя ряд на абсолютную сходимость (см. задачу 60), составим ряд из модулей
.
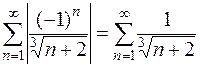Для сравнения возьмем обобщенный гармонический расходящийся ряд 
и воспользуемся предельным признаком сравнения [приложение 5 – РЯДЫ]:
.
Так как предел конечен и отличен от нуля, то ряды
и
ведут себя одинаково в смысле сходимости, т.е. ряд тоже расходится. Итак, ряд 
расходится, следовательно, ряд 
сходится условно.
Задача 62. Исследовать на сходимость ряд 
.
Решение. Если ряд сходится, то 
(см. задачу 54). Но 
(этот предел не существует), поэтому ряд расходится.
Задача 63. Исследовать на сходимость ряд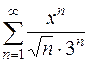 
.
|
|
|
Решение. Ряд вида
,
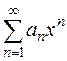где а 0, а 1, а 2, …, аn, …–постоянные вещественные числа, называется степенным рядом. Степенной ряд – это частный случай функционального ряда 
, то есть ряда, члены которого есть функции, зависящие от х.
Для каждого степенного ряда существует положительное число R такое, что этот ряд абсолютно сходится, если 
и расходится, если 
. Число R называется радиусом сходимости рассматриваемого ряда, а интервал (– R, R) – интервалом сходимости этого ряда.
На концах интервала сходимости (в точках х = – R и х = R) степенной ряд может сходиться или расходиться. Это выясняется отдельно для каждого числового ряда, получающегося из степенного ряда в результате подстановки в него указанных значений.
Радиус сходимости R степенного ряда можно определить с помощью признака Даламбера или радикального признака Коши по формулам [приложение 5 – РЯДЫ]:
, 
.
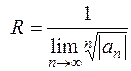Найдем радиус сходимости для заданного ряда по первой формуле. Так как
, 
,
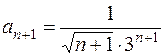получим
.
Следовательно, R = 3. Поэтому данный ряд абсолютно сходится в интервале (– 3; 3) и расходится вне отрезка [– 3; 3].
Исследуем сходимость ряда в точках х = 3 и х = – 3.
При х = 3 исходный ряд принимает вид
.
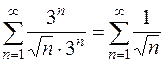Это обобщенный гармонический расходящийся ряд (
) [приложение 5 – РЯДЫ]. Итак, при х = 3 заданный ряд расходится.
При х = – 3 получаем знакочередующийся ряд
.
Рассмотрим для него выполнение условий теоремы Лейбница [приложение 5 – РЯДЫ]
1) 
; 2) 
.
Условия выполняются, значит, ряд 
сходится.
Следовательно, область сходимости исходного ряда [– 3; 3).
Задача 64. Исследовать на сходимость ряд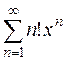 
.
Решение. Этот ряд степенной. Будем искать радиус сходимости ряда по формуле
(см. задачу 63).
Так как 
, 
, то
.
Это означает, что областью сходимости ряда может быть только одна точка х = 0. Действительно, при х = 0 получим нулевой сходящийся ряд
0 + 0 + 0 + ….
Итак, ряд 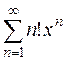сходится в одной точке х = 0.
Задача 65. Исследовать на сходимость ряд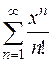 
.
Решение. В соответствии с теорией, изложенной в задаче 63, будем искать радиус сходимости ряда по формуле
.
Так как 
, 
, то
.
Следовательно, 
. Значит, ряд сходится при любых х и область сходимости ряда 
.
|
|
|
