Рис. 1. Схема течения в диффузоре: I - зона ускорения, II - частичное торможение в диффузоре с кажущимся охлаждением и восстановлением давления до атмосферного, III – течение при постоянном давлении с обратным притоком тепла.

Рис. 1. Схема течения в диффузоре: I - зона ускорения, II - частичное торможение в диффузоре с кажущимся охлаждением и восстановлением давления до атмосферного, III – течение при постоянном давлении с обратным притоком тепла.

В условиях отсутствия вязкости теоретически полное давление в диффузорах может восстанавливаться до начального давления покоя - иными словами, в отсутствие трения газ можно бесконечно качать из одного резервуара в другой путём ускорения и торможения потока, при этом давления в резервуарах могут быть одинаковыми. В случае наличия вязкости и отсутствия теплопроводности давление в диффузоре не может восстановиться в полной мере, и газ может течь бесконечно только в том случае, если давление во втором резервуаре будет ниже, чем в первом. Это суждение полностью вкладывается в рамках принятых теоретических представлении. Согласно уравнению производства энтропии, как для закрытых, так и для открытых систем наличие вязкости всегда приводит к росту энтропии вдоль течения ( 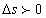), а следовательно, давление торможения потока 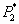(не говоря уже о статическом давлении ) на выходе из диффузора (в сечении 2-2 рис. 1. ) всегда ниже исходного ( ):

(1)

Таким образом, при традиционно малой теплопроводности газа учёт вязкости в задачах гидро-аэродинамики всегда даёт результат, который не нарушает гармонию классической науки. Но что будет, если свойства распределены обратно? Давайте представим, что вязкость нашего газа пренебрежимо мала, а теплопроводность - высока. Несмотря на то, что в природе такие газы еще не найдены, такой теоретический эксперимент имеет весьма интересный характер: оказывается, что генерация полезной энергии из равновесного пространства затрудняется только из-за того, что не имеется соответствующих веществ, а основным препятствием является высокая вязкость при сравнительно низкой теплопроводности газов. И даже если никогда не удастся найти подходящие рабочие вещества, теоретический результат такого численного эксперимента является поразительным и весьма важным, так как он в корне разрушает второй закон и теорему Карно о том, что предельная эффективность преобразования тепловой энергии не зависит от тепловых свойств, поэтому якобы не имеет смысл искать оптимальные вещества.

Чтобы доказать обратное, мы предлагаем рассмотреть и оптимизировать простейший процесс ускорения и торможения в диффузоре газа с высокой теплопроводностью. К примеру, положим, что мы имеем газ с параметрами воздуха, но при коэффициенте теплопроводности 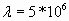w/m*K. Для моделирования течения такого газа в уравнениях сохранения массы, энергии и количества движения необходимо учесть наличие существенного теплового потока - тогда они имеют вид:

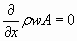(2)

(3)

 (4)

Здесь - площадь поперечного сечения потока. Данную систему можно преобразовать с учетом известного термодинамического тождества и зависимости между параметрами состояния:

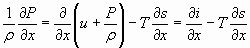 (5)

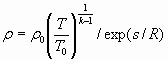. (6)

Тогда исходная система принимает вид:

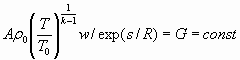(7)

 (8)

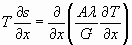 (9)

Таким образом, мы имеем три уравнения при четырех неизвестных при этом площадь сечения потока можно отнести к граничным условиям: задавая изменение площади сечения потока вдоль координаты , данные три уравнения позволяют однозначно определить три основных параметра потока. Однако, для облегчения поиска оптимального решения мы применяем несколько иной подход - задаём характер зависимости энтропии от температуры и ищем такой характер изменения площади , который обеспечивает такое течение. В таких условиях из исходной системы выпадает энтропия, а система (7-9) однозначно определяет тройку параметров . С учетом отмеченного, мы ищем желаемый для нас термодинамический процесс ускорения и торможения потока, когда его расход составляет kg/s.

Ускорение потока. При рассмотрении процесса ускорения потока в соплах в условиях низкой теплопроводности газа считают, что энтропия, как минимум, не уменьшается - данный процесс в координатах выражают вертикальной или отклоненной в сторону роста энтропии линией. При сильной теплопроводности возникновение продольных потоков тепла и перераспределение энергии радикально меняет картину. Ускорение газа с сильной теплопроводностью может происходить с разными режимами изменения параметров течения, в зависимости от формы суживающегося канала (сопла), и главная особенность такого ускорения заключается в снижении энтропии.

С точки зрения точного аналитического решения исходной системы, заслуживает внимание процесс ускорения с постоянной теплоёмкостью - к примеру, можно рассмотреть течение с изохорным ускорением , что целесообразно и с точки зрения поиска оптимального решения. В таком случае в исходной системе (7-9) можно полагать существование следующей зависимости энтропии от температуры:

. (10)

В таких условиях система решается аналитически, и легко находится характер изменения всех параметров в зависимости от продольной координаты - в частности, связь между температурой и продольной координатой имеет вид:

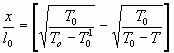 (11)

где - начальная температура газа перед ускорением, - температура в начальном сечении суживающегося канала,

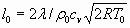(12)

Решение системы даётся в таблице 1. Ускорение при происходит в канале длиной несколько сотен метров, что обусловлено высокой теплопроводностью и, соответственно, высоким значением линейного масштаба .

Таблица 1.

	D	T	P	s	w	ρ w	-gradT	q	qA/G
0. 0	0. 2096			-2. 497	23. 96	28. 99	0. 00416
203. 1	0. 1593			-7. 518	41. 5	50. 2	0. 02163
310. 6	0. 1247			-20. 22	67. 76	81. 98	0. 09418
347. 2	0. 1104			-33. 16	86. 38	104. 5	0. 1951
367. 2	0. 1018			-46. 34	101. 6		0. 3179
380. 3	0. 09573			-59. 76	114. 9		0. 4591
389. 7	0. 09114			-73. 43	126. 8		0. 6167
396. 9	0. 08747			-87. 38	137. 6	166. 5	0. 7891
402. 6	0. 08444			-101. 6	147. 7	178. 7	0. 975
407. 2	0. 08187			-116. 1	157. 1		1. 174
411. 2	0. 07965			-130. 9		200. 8	1. 384
414. 5	0. 0777			-146	174. 4		1. 606
417. 4	0. 07597			-161. 5	182. 5	220. 7	1. 839
420. 0	0. 07441			-177. 3	190. 2	230. 1	2. 081
422. 2	0. 073			-193. 4	197. 6		2. 334
424. 3	0. 07172			-209. 9	204. 7	247. 7	2. 596
425. 4	0. 071			-220	208. 9	252. 7	2. 758

Данные в таблице имеют следующие размерности:

x - расстояние от начального сечения – м,

D - диаметр потока – м,

P - давление потока – Па,

w - скорость - м/с,

gradT - градиент температуры - K/м,

q - удельный тепловой поток - ,

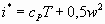- энтальпия торможения - .

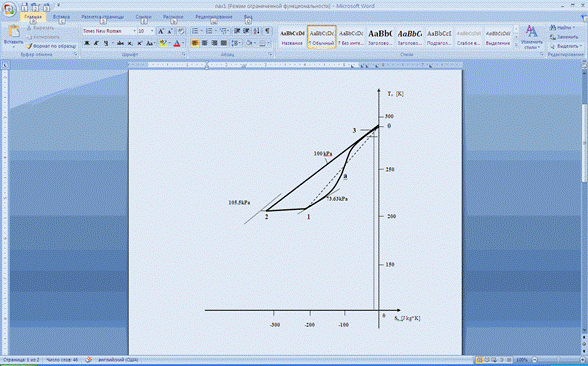
В 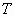- координатах процесс изохорного ускорения выражается прерывистой линией 0-1 (рис. 2).

Предложенное выше решение заслуживает внимание в том смысле, что оно является точным и наглядно показывает снижение энтропии в теплоизолированном течении из-за возникновения нарастающего продольного потока тепла 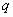. Вместе с тем, получение таких параметров потока в граничном сечении 1-1 (точка 1 на рис. 2. ) можно обеспечить в условиях весьма различных процессов. Рассмотрим любой процесс ускорения покоящегося потока. Решая уравнение (9) для произвольного процесса ускорения теплопроводного газа, получим:

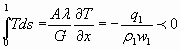. (13)

где и - удельные поток массы и тепла в сечении 1-1 в ускоренном потоке. Таким образом, если при ускорении в различных условиях в результате получается течение, которое характеризуются одинаковыми удельными потоками массы и тепла, то эти различные процессы будут характеризоваться одинаковым значением интеграла 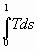. При этом, как видно, данный интеграл имеет строго отрицательное значение, из чего следует важное заключение:

Если маловязкий газ обладает высокой теплопроводностью, то его ускорение (истечение из большого объема или поступление из резервуара в канал) всегда приведёт к снижению энтропии - в терминах В. Шаубергера такой процесс можно назвать имплозией. Допустим, в конце процесса ускорения на входе диффузора мы имеем тепловой поток и удельный поток массы 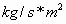при температуре и энтропии 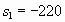J/kg*K, в таком случае данные параметры могут быть достигнуты после любого процесса ускорения, для которого справедливо условие:

.

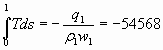
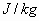Следовательно, такой режим не требует в обязательном порядке применения длинного канала - поток может ускоряться и в другом режиме или суживающемся канале произвольной конфигурации.

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: