Рис.2. диаграмма термодинамического цикла «странного» диффузора: 0-1- ускорение теплопроводного газа в длинном сопле при постоянной теплоемкости. 0-а-1 – ускорение потока вблизи входного сечения. 1-2-частичное торможение в диффузоре с кажущимся охлаждение

Рис. 2. диаграмма термодинамического цикла «странного» диффузора: 0-1- ускорение теплопроводного газа в длинном сопле при постоянной теплоемкости. 0-а-1 – ускорение потока вблизи входного сечения. 1-2-частичное торможение в диффузоре с кажущимся охлаждением и восстановлением давления до атмосферного. 2-3-процесс обратного притока тепла в открытом пространстве. 3-0 – нагрев отработанного воздуха из окружающей атмосферы.

Процесс ускорения в условиях пространственного течения, как это обычно имеет место вблизи входного сечения различных установок (область I вблизи сечения 1-1 на рис. 1), может решаться только численно. Не затрачивая усилия на решение такой пространственной задачи, из условия (13) мы уже знаем, что такому процессу будет соответствовать линия типа 0-a-1 на рис. 2, площадь под которой совпадает с площадью под прерывистой линией 0-1. Таким образом, после ускорения различным способом (с применением монотонно суживающегося канала или без него) на входе в диффузор мы можем иметь режим течения:

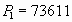K, Pa, 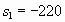J/kg*K, m/s, . (14)

Течение в диффузоре, торможение. Рассмотрим теперь процесс течения в диффузоре (область II на рис. 1). Граничные условия на входе известны из (14). Для расчёта процесса торможения и размеров подходящего диффузора вновь зададим оптимальную зависимость энтропии от температуры (линия 1-2 на рис. 2):

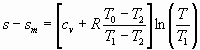, (15)

где K – температура потока на выходе из диффузора (падение температуры задаём произвольно). Интегрирование исходной системы уравнениё для процесса торможения осуществляется с применением численных методов - в таблице 2 даётся результаты расчёта всех параметров. Легко можно убедиться, что численные данные потока в любом сечении удовлетворяют всем требованиям законов сохранения массы, энергии и импульса. Тепловой поток направлен вдоль течения в сторону падения температуры. «Странность» предложенного решения заключается в том, что оно допускает снижение энтропии вдоль изолированного потока (как нарушение принципа перманентного роста энтропии), а процесс полного торможения приводит к повышению давления потока до Pa - таким образом, применение диффузора позволяет нагнетать газ из объёма с давлением 100000Pa (или из атмосферы) в объём с более высоким давлением.

Теперь рассмотрим участок диффузора длиной 0. 6267м - как видно из предложенного решения (таблица 2), на данном расстоянии от входа статическое давление потока равно атмосферному, а следовательно, такой диффузор может бесконечно качать газ между объемами с одинаковым давлением. Вместе с тем, на выходе из диффузора будет довольно высокая скорость ( ) и кинетическая энергия потока.

Посмотрим, что происходит в открытом пространстве, в которое диффузор выбрасывает газ с напором и тепловой поток .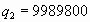

Таблица 2.

	D	T	P	s	w	ρ w	-gradT	q	qA/G
0. 0	0. 071			-220	208. 9	252. 7	2. 758
0. 0717	0. 07157	211. 8		-231. 2	198. 1	248. 7	2. 833
0. 1421	0. 07236	211. 6		-242. 5	186. 8	243. 3	2. 887
0. 2116	0. 07345	211. 4		-253. 7	174. 7	236. 1	2. 914
0. 2807	0. 07494	211. 2		-265	161. 8	226. 8	2. 908
0. 3501	0. 077			-276. 3	147. 7	214. 9	2. 857
0. 4213	0. 07993	210. 8		-287. 6	132. 1	199. 4	2. 746
0. 4961	0. 08431	210. 6		-298. 9	114. 4	179. 2	2. 554
0. 5787	0. 09159	210. 4		-310. 3	93. 4	151. 9	2. 236
0. 6267	0. 0977	210. 3		-316	80. 55	133. 47	1. 998
0. 6792	0. 1069	210. 2		-321. 5	66. 05	111. 43	1. 694
0. 906		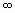		-332. 9

Нагрев газа при постоянном давлении и получение полезной энергии. Диффузор длиной 0. 6267 м выбрасывает в окружающее пространство (с давлением 100000 Pa и температурой 288 K) газ с температурой =210, 3 K - естественно, что такая струя будет нагреваться. При этом нагрев может осуществляться до температуры окружающего пространства как за счёт тепла окружающей среды, так и за счёт потока тепла из диффузора 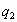. После получения тепла 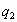температура струи поднимется (область III на рис. 1 и линия 2-3 на рис. 2) до значения:

=210, 3 + 9989800*0, 007493/(1*1005) = 284, 8 K (16)

При этом, согласно уравнениям движения, в пространстве с одинаковым давлением газ не меняет скорость и в сечении 3-3 струя будет иметь заметную кинетическую энергию - если данная энергия не будет использована, то по мере торможения потока температура восстановится полностью до 288 K. Однако кинетическая энергия потока в свободном пространстве может быть использована в виде механической энергии, в таком случае отработанный газ будет иметь температуру 284, 8 K, т. е. газ будет холоднее, чем в начале процесса. Теоретически максимальная энергия, которую может дать наш конкретный диффузор, равняется:

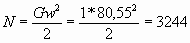
(17)

Естественно, что при наличии вязкости и потерь данная мощность будет ниже, но мы получили настолько заметную энергию, что трение не сможет значительно снизить столь существенный эффект.

Приведенный нами наглядный пример показывает, как подтверждение справедливости предложенной нами Ge - теоремы [3], что налицо явное противоречие в науке. Решение данного конфликта законов возможно только путем отказа от существующих в классической науке представлений, так как теория Карно является результатом простой, грубой схематизации процессов в замкнутой системе «источник тепла - рабочее тело – охладитель». Если учесть, что, помимо теплоёмкости, реальные вещества имеют и другие механизмы внутренней аккумуляции и циркуляции энергии, то становится очевидным, что теоретически нет необходимости применять внешний охладитель - в этом заключается основная ошибка теории Карно. Как мы показали, тепловые установки в действительности могут работать в другой системе: «источник тепла - рабочее тело». По нашему мнению, данная часть классической термодинамики основывается на глубоко замаскированной ложной циклической логике (говоря иначе, на алогичности): если внимательно проанализировать предложенные в термодинамике суждения, то обнаруживается, что при доказательстве теоремы Карно обязательно используется второй закон, а при доказательстве второго закона - применяют принцип Карно (или, попросту говоря, основываются на чисто “априорных“ соображениях, как это делается в формулировке Клаузиуса о стремлении тепла в сторону уменьшения температуры). Мы показали, что теплопроводное вещество при целенаправленном, обдуманном вмешательстве человека может самостоятельно двигаться к области высокого давления - значит, при всём уважении к Клаузиусу, при специальных условиях и тепло может двигаться в сторону высокой температуры путём создания соответствующих устройств, не потребляющих энергию - в историческом контексте, первым простейшим устройством такого характера была бы сортирующая перегородка Максвелла, имеющая свойства односторонней проводимости быстрых молекул без всяких датчиков и дополнительных устройств (как это необоснованно и настойчиво требуют противники Максвелла). Предложенный нами диффузор также без всяких дополнительных энергопотребляющих устройств является ещё одним и, к счастью, не единственным доказательством того, что идея гениального шотландца была отвергнута напрасно, и в этом состоит судьбоносная ошибка нашей цивилизации, решившей обеспечивать развитие нашей планеты беспощадным истреблением природных ресурсов.