Рис.1. Диаграмма цикла с чередованием эндотермического (0-1) и экзотермического (2-3) процессов.

Рис. 1. Диаграмма цикла с чередованием эндотермического (0-1) и экзотермического (2-3) процессов.

При исчезновении тепла постоянство температуры будет соблюдаться в случае одновременного сжатия газа (линия 0-1). Учитывая, что в таком процессе теплоёмкость, в принципе, может меняться, работа сжатия, которая тратится в данном процессе, согласно (13), имеет вид:

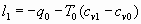. (15)

В дальнейшем газ сжимается изолированно, до температуры T_max, без всяких внешних и внутренних источников. Работа сжатия имеет вид:

. (16)

При температуре T_max осуществляется обратный химический или другой процесс, при котором вновь выделяется потребленное тепло. Работа процесса имеет вид:

. (17)

В результате изоэнтропного расширения температура вновь падает (точка 4) и совершается работа:

. (18)

Если просуммировать все затраты механической энергии до состояния 4, то получим простую формулу:

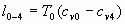. (19)

Но в точке 4, после совершения обратного процесса химический состав среды восстановлен и, при одинаковой температуреT₀, теплоёмкости тоже одинаковы, поэтому имеем:

. (20)

Вместе с тем, как видно, в точке 4 газ имеет избыточное давление, поэтому при возвращении в исходное состояние он может совершать работу в условиях постоянной температуры:

. (21)

Причём из уравнения энергии (13) следует, что данная работа совершается за счёт притока тепла извне:

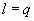. (22)

.

Рис. 2. Диаграмма цикла с чередованием процессов имплозии (линия 0-1) и выделения тепла (линия 1-2).

Если уравнение (9) умножить на температуру и проинтегрировать по замкнутому контуру, то можно убедиться, что площадь диаграммы циклов в координатах T-s’ выражает работу, поэтому имеем:

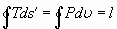. (23)

Следовательно, процессы с внутренними превращениями удобнее выразить в T-s’ координатах.

Таким образом, любой цикл с чередованием внутренних процессов поглощения и выделения тепла будет демонстрировать аналогичный результат (Рис. 2), и это подтверждает, что такие процессы дают возможность генерации энергии из тепла. Нет сомнения, что данный цикл оставался без внимания из-за противоречия с принципом Карно и со вторым законом термодинамики: согласно данному закону, представленные на рис. 1 и на рис. 2 циклы попросту не могут существовать. Следуя второму закону термодинамики, если в системе физических тел совершается химическая реакция с поглощением тепла при определенной температуре, то обратная реакция с выделением тепла должна протекать только при более низкой температуре. Насколько нам известно, справедливость такого принципа не доказана и не может быть доказана, так как в реальности обнаруживаются противоположные эффекты.

Рис. 3. Диаграмма цикла генерации водорода и кислорода путем распада воды.

Теперь, на основе проведённого выше анализа, рассмотрим следующий цикл (Рис. 3). Допустим, в точке 0 мы имеем 1 килограмм воды, в обычных условиях P₁　 =　 10⁵ Па, T₀　 =　 298K. Из данного состояния в адиабатном процессе 0-1 давление можно снизить до P₁　 =　 0. 02*10⁵ Па. При таком давлении температура кипения воды падает до 17, 2°C. В таком состоянии возникают пары воды в виде пузырьков, и будем иметь смесь воды и пара со степенью сухости x₁ =　 0, 0434. В условиях низкого давления и температуры жидкость может вскипеть полностью (x =　 1), если происходит подвод соответствующей энергии (линия 1-2). При отмеченных параметрах состояния удельная теплота парообразования составляет r = 2460 кдж/кг.

Естественно, если внутри воды имеются условия для активации вакуума, то в качестве такого источника для кипения может послужить и энергия вакуума, но паро-жидкостная смесь вполне может нагреваться и за счет тепла окружающей среды - путём теплообмена с окружающим пространством. Тогда в правой части уравнения (10) будет фигурировать только последний член, а из уравнения (9) следует, что

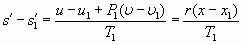, (24)

Если в процессе теплообмена 1 кг смеси получит 2353 кдж тепла, то жидкость полностью испарится (процесс 1-2). Далее, при имеющихся значениях давления и температуры можно осуществить эндотермический процесс разложения воды на водород и кислород. Эндотермический процесс распада требует дополнительную энергию, однако, если отсутствует внешний приток тепла, то определённая часть воды может разлагаться за счёт тепла конденсации другой части. Для расчёта данного процесса следует учесть, что удельное тепло, которое требуется для энергетического обеспечения процесса распада воды, равняется Δ H=15878 кдж/кг - следовательно, для получения 0, 1341 кг смеси кислорода и водорода нужно иметь 2130 кдж. Такое количество энергии может выделить 0, 8659 кг сухого водяного пара при конденсации - таким образом, в процессе 2-3 основная часть пара (0, 8659 кг) может превратиться в жидкость с выделением 2130 кдж. тепла, а остальная часть пара (0, 1341 кг), за счёт данной энергии, можеть распадаться с выделением кислорода и водорода, в результате чего в точке 3 будем иметь 119, 2 гр кислорода, 14, 9 гр водорода и 865, 9 гр. воды в жидком состоянии. Иными словами, в точке 3 мы вновь будем иметь газожидкостную смесь со степенью сухости x₃=0, 1341, но с той разницей, что вместо пузырьков водяного пара мы будем иметь пузырьки горючей смеси.

Эндотермический процесс разложения воды 2-3 является обратным процессом взрыва - для обозначения подобных процессов Виктор Шаубергер ввёл понятие имплозии. Мы предлагаем назвать таким термином любой теплоизолированный процесс, в котором происходит уменьшение энтропии. Линия 2-3 выражает имплозию в терминах Шаубергера - это является процессом кажущегося охлаждения, когда тепло уходит не в окружающую среду а “прячется” внутри молекул в результате химических превращении. Для такого процесса уравнение (10) даёт:

. (25)

Или, с учётом известного значения теплового эффекта химической реакции (энтальпии) :

. (26)

В точке 3 смесь вновь будет иметь низкое давления и температуру. При адиабатном сжатии до исходного атмосферного давления (процесс 3-4) температура смеси воды и пара могла бы подняться до 85 градусов Цельсия, но пары кислорода и водорода не могут конденсироваться, так как они имеют более низкие температуры кипения, чем вода. В результате адиабатного сжатия температура смеси газов повысится, а температура воды останется в пределах 17, 2°C. После теплообмена с пузырьками пара гремучего газа температура жидкости повысится, но незначительно (точка 5).

Таким образом, 1 килограмм воды после снижения и повышения давления может выделить в окружающую атмосферу 14, 9 гр водорода и 119, 2 гр кислорода (данное количество может меняться в зависимости от минимального давления), а при сжигании данной смеси может выделяться тепло в количестве 2130 кдж. Допустим, что мы имеем тепловой двигатель, который (в худшем случае) превращает в механическую работу только 1/3 данной энергии, в таком случае мы получим 710 кдж механической работы. А теперь посмотрим, каковы расходы для осуществления отмеченного цикла 012350: данная работа меньше площади цикла 012340 - нетрудно подсчитать, что lp = 28, 3 кдж, следовательно, полезная механическая энергия более чем в 20 раз больше, чем затраченная. Таким образом, мы показали на примере разложения воды, что путём внутренней циркуляции энергии с использованием химических процессов можно генерировать полезную энергию из тепла окружающей среды. Данный цикл позволяет обосновать реальность работы «странных» тепловых насосов Григса или Потапова: например, если смесь води и пара сжимается не до атмосферного давления, а значительно сильнее, то пузырьки гремучего газа могут взрываться внутри воды, выделяя огромное количество тепла - в частности, выделяемое 1 кг воды количество гремучего газа достаточно для того, чтобы довести до кипения 6-7 кг. Воды, чем и объясняются странные показатели указанных тепловых насосов.

　

⇐ Предыдущая11121314151617181920Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: