 |
Формирование понятия «задача»
|
|
|
|
В настоящее время в школьной практике господствует обучение решению задач на основе введения ранней их типизации. Эта тенденция еще усилилась с ведением новых программ благодаря определенной алгебраизации курса.
Такой путь обучения дает результаты в том смысле, что ученик быстро справляется с задачей, если он может определить тип, к которому она относится. Однако этот путь препятствует самостоятельному мышлению школьников. Они оказываются беспомощными, когда встречаются с необычной задачей, если даже по трудности она не превосходит тех, которые решались раньше.
Вместе с тем детей совсем почти не обучают правильной работе с текстом задачи. Им сообщают термины: «условие», «вопрос», «данные числа» и «неизвестное число», но их смысл и взаимосвязь не раскрываются. Между тем проникновение в характер связей между частями задачи – первый шаг к проникновению в ее смысл.
Чтобы успешно работать с текстом, ученик должен иметь ясное понятие задачи, из каких частей она состоит и какую информацию несет в себе каждая часть. Он должен уметь найти условие и вопрос задачи, как бы они ни располагались в тексте и в какой бы форме не были даны. Должен также находить данные, содержащиеся в тексте, и понимать, что является искомым.
Вопросам решения арифметических задач в начальных классах посвящено значительное количество статей и книг. В них рассматриваются различные вопросы методики обучения школьников решению задач. Есть работы, в которых освещаются те или иные стороны психологии решения задач.
Нельзя не отметить крайней бедности фактического материала, добытого путем экспериментального исследования. Характерно преобладание методических указаний учителю без сравнения с другими методическими подходами и обоснования фактами, раскрывающими процесс овладения решением арифметических (математических) задач. Это особенно заметно в методических пособиях, изданных к новым программам для начальных классов. Так, например, в книге «Методика преподавания математики в начальных классах» даны рекомендации, относящиеся к первому этапу обучения – решению простых задач. В дальнейшем выдвигаются требования к методике работы над составными задачами, а также применительно к другим вопросам методики. Привлекает внимание подчеркивание необходимости постоянных упражнений для понимания и овладения умениями решения задачи.
|
|
|
Имеются попытки объединения методики и психологии обучения арифметике. К ним относится, в частности, книга «Вопросы методики и психологии обучения арифметике в начальных классах». В главе, посвященной решению задач, авторы специально останавливаются на анализе умения решать задачи. Здесь есть попытка сформулировать правила, которыми должны руководствоваться школьники при решении задач. На разных этапах обучения по мере усложнения решаемых задач на первый план выступает та или иная операция (или их совокупность), которая нуждается в специальной «отработке». О необходимости «отработки» при формировании умения решать задачи упоминается и в другом контексте. Эти требования перекликаются с утверждениями о необходимости постоянных упражнений для формирования умения решать задачи, содержащимися в «Методических указаниях», о которых говорилось выше. В ряде зарубежных публикаций значительное место уделяется мыслительным процессам при решении арифметических задач. Это имеет место, например, в книге Д. Пойа 176. В работе Л. Еленьской раздел «Формирование математического мышления» написан целиком на материале решения арифметических задач в начальных классах. В этом разделе рассматриваются трудности в решении задач, составление задач, типы задач, исправление ошибок. По мнению автора, учителя рассуждают с детьми главным образом при составлении задач, а не при их решении.
|
|
|
В упомянутых работах, а также в других книгах и статьях, с которыми мы ознакомились (см. список литературы в конце данной книги), пет исследования, где изучалось бы формирование у младших школьников понятия об арифметической задаче. Имеются исследования формирования понятия о типе задачи (подразумеваются типовые задачи). Упомянем здесь о содержательном исследовании 3. И. Калмыковой.
Наше исследование имеет своей целью выяснить, как происходит усвоение понятия «задача» учащимися экспериментальных и обычных классов.
В качестве критерия усвоения нами было взято применение полученных теоретических знаний о задаче в ее решении.
В соответствии с программой начальных классов179 нами были выделены четыре признака задачи: наличие условия, вопроса, данных и искомого. Разработаны тексты заданий и инструкция к ним. Поскольку исследование рассчитано на школьников I, II и III классов, задания различны по степени трудности.
Задание 1
1.Для букета сорвали 7 ромашек и 8 колокольчиков. Сколько Всего цветов сорвали для букета?
2.В корзинке лежало '15 огурцов. 9 огурцов вынули.
3. Миша нашел 4 белых гриба и 10 подберезовиков. Сколько подберезовиков нашел Миша?
4.4 + 6. Сколько получится?
5.Ученики первого класса должны сделать 19 игрушек. Они уже сделали 11 игрушек. Сколько игрушек им еще осталось сделать?
6.На столе лежали ложки, вилки и ножи. Сколько всего на столе ложек, вилок и ножей?
Задание 2
1.Когда от мотка ленты отрезали 9 м, в нем осталось 17 м. Сколько метров ленты было в мотке?
2.Мама принесла 3 кг яблок, 1 кг она положила в вазу.
3.У портного было 9 м сатина. Из 7 м он сшил сарафаны. Найди остаток сатина.
4.Сколько флажков сделали ребята к празднику 1 Мая?
5.В саду посадили 19 яблонь и 23 вишни. Сколько посадили в саду яблонь?
6.Магазин продал в первый день 11 коробок карандашей. Сколько коробок карандашей продал магазин в два дня, если во второй день он продал 17 коробок?
Задание 3
1.В бидоне было 14 л молока. Сколько литров молока отлили из бидона, если в нем осталось 5 л?
|
|
|
2.Маша взяла в библиотеке книгу, в которой было 47 страниц. В первый день она прочла 10 страниц, а во второй – на 3 страницы больше.
3.В зал принесли 72 стула и расставили их в 8 рядов. Сколько стульев расставили в зале?
4.Отряд пионеров отправился в поход. В первый день пионеры прошли 15 км, во второй – 17 км. Найди расстояние, которое прошли пионеры в два дня.
5.У учительницы были тетради в Линейку и в клетку. Она раз
дала их ученикам. Сколько тетрадей получил каждый ученик?
6.Сколько денег заплатили за мишку и куклу, если мишка стоил 2 руб., а кукла в 3 раза дороже?
Задание 4
1.Три звена вместе собрали 58 кг семян. Сколько семян собрало третье звено, если первое собрало 15 кг, а второе на 4 кг больше?
2.Из двух городов навстречу друг другу вышли два автомобиля. Первый шел со скоростью 40 км/ч. Скорость второго на 6 км больше. Через 8 ч они встретились.
3.Школьники посадили в три дня 390 деревьев. В первый день они посадили 120 деревьев, во второй – на 5 деревьев больше, чем в первый. Сколько деревьев посадили школьники в три дня?
4. Периметр прямоугольника 74 см. Вычисли площадь прямо угольника, если его основание равно 26 см.
5. Сколько тонн свеклы собрали, если ее собирали с разных участков?
6. Какое расстояние проехал путешественник, если он сначала ехал 3 ч на лодке со скоростью 8 км/ч, а затем 4 ч на пароходе со старостью 27 км/ч?
Задание 5
1. Сколько израсходовали ткани на пошив 17 платьев, 29 блузок и 13 пальто, если на каждую блузку пошло 190 см ткани, на платье – в два раза больше ткани, чем на блузку, а на пальто – на 30 см меньше, чем на платье?
2. Из Москвы во Владивосток вылетел самолет. Первые 3 ч он летел со скоростью 950 км/ч, а остальной путь – со скоростью 1000 км/ч. Определи скорость, с которой летел самолет в первый час пути, если расстояние от Москвы до Владивостока около 8000 км?
3. В одной рукописи было 240 страниц, в другой – 3120 страниц, а в третьей – 480 страниц. Сколько потребовалось дней, чтобы при одной и той же производительности труда перепечатать все три рукописи, если третью рукопись перепечатывали на 4 дня дольше, чем вторую?
|
|
|
4. Чтобы сплавить по реке бревна, их связывают в плоты. В мае сплавили 86 плотов, а в июле – 98 таких же плотов, и оказалось, что в июле сплавили на 28&0 бревен больше, чем в мае.
5. Диванную подушку обшили шнуром. Вдоль ребра шнур пришивали гладко, а в каждом уголке сделали петлю. Сколько пошло шнура на обшивку подушки?
6. Найди длину каждого из двух кусков телеграфного провода, если их длина вместе равна 16 м, и один кусок весит 1 кг 240 г, а другой – 1 кг 440 г.
Каждое задание содержит шесть текстов. Некоторые из них являются задачами, остальные не представляют собой задач, так как в них отсутствует один или два необходимых признака. Каждое следующее задание сложнее предыдущего. Усложнение текстов, являющихся задачами, происходит за счет увеличения объема и усложнения структуры. Усложнение структуры текста достигается, во-первых, перенесением части условия или всего условия в предложение, содержащее вопрос задачи, и во-вторых, выражением вопроса при помощи повествовательного предложения.
Усложнение текстов, не являющихся задачами, происходит в основном за счет увеличения объема. Исключением являются тексты, не содержащие искомого. В них большую роль играет расположение числа и формального вопроса, в котором предлагается найти это число. Так, в первом задании вопрос следует непосредственно за числом, в каждом следующем дистанция увеличивается и уже в четвертом задании достигает 16 слов.
Каждое задание выполняли все ученики класса. Работа проводилась следующим образом: экспериментатор читал вслух каждый текст задания, ученики должны были внимательно прослушать его, обдумать и поставить на листе бумаги знак плюс (-}-), если это задача, и знак минус (–), если это не задача.
Затем из каждого класса по рекомендации учителя отбиралось 18 учеников для индивидуальной беседы. Из них 6 хорошо успевающих, 6 среднеуспевающих и 6 слабоуспевающих. Цель беседы – установить, на основании каких признаков выполнено задание. Беседа проводилась таким образом: экспериментатор еще раз читал ученику каждый текст, предлагал подумать и сказать, задача это или не задача, а затем рассказать, почему ученик так думает. Никаких дополнительных, наводящих вопросов, никому из учеников не задавалось.
Задания давались в экспериментальном классе в конце первого года обучения, в начале и конце второго года обучения и в начале третьего года обучения (школа № 125 Москвы, 1967–1969 гг.).
Количественные результаты анализа работ по допущенным ошибкам представлены в таблице 3318° (по предварительным опытам).
|
|
|
Таблица 33
Рассмотрим, как происходило качественное изменение ответов учеников во время индивидуальных бесед. Для оценки нами были выделены две основные линии: полнота обоснования и широта охвата признаков.
Для прослеживания первой линии нами были проанализированы ответы, являющиеся доказательством того, что данный текст – задача. Такой выбор объясняется тем, что для полного ответа в такой ситуации необходимо привлечение всех известных школьникам основных признаков.
В таблице 34 представлены данные, характеризующие полноту обоснования текстов задач в том же классе школы № 125.
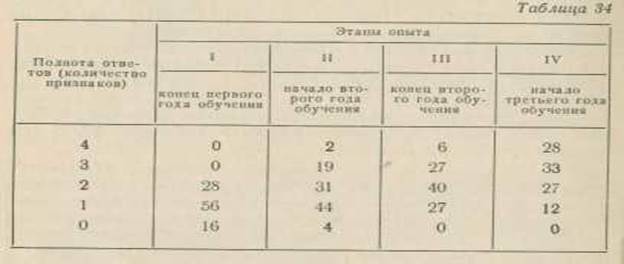
Анализ приведенных данных говорит о том, что в этом классе происходит непрерывный процесс углубления понятия «задача», не прекращающийся и в период летних каникул, что подтверждается сравнением результатов по годам обучения.
Обратимся ко второй линии, характеризующей качественные сдвиги в ответах школьников, – к широте охвата признаков. Под широтой охвата признаков мы понимаем количество различных признаков, привлеченных учеником во всех ответах на данном этапе. Этот показатель может совпадать с показателем полноты обоснования, а может быть и шире этого показателя.
В таблице 35 приведены данные о широте охвата признаков.
Как видно из данных, приведенных в таблицах 33, 34, 35, ученики этого класса довольно успешно овладевали понятием «задача». На каждом следующем этапе
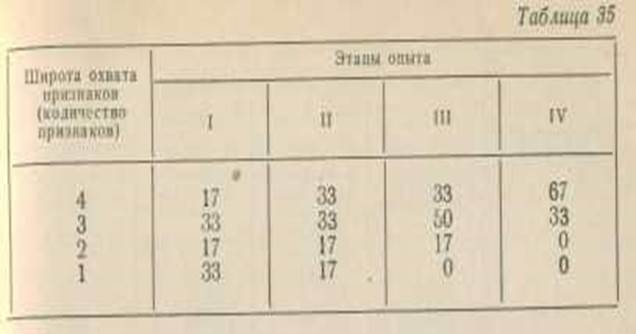
опыта все показатели овладения понятием возрастают и к началу третьего года обучения достигают высокого уровня.
Особенно это относится к количеству правильно выполненных работ (70% всех работ выполнены безошибочно) и широте охвата признаков (67% учеников в своих ответах верно использовали все четыре основных признака).
Несколько хуже обстоит дело с полнотой обоснования. Только 28% ответов содержат все четыре признака и 33% – три признака. Это свидетельствует о том, что дети еще не умеют всесторонне рассматривать предложенный текст.
Основные опыты проводились в 1969–1971 гг. в экспериментальном классе школы № 3 г. Тулы, школы № 2 г. Шатуры Московской области и в обычном классе школы № 589 Москвы.
Рассмотрим, как протекал процесс усвоения интересующего нас понятия в каждом из взятых для изучения трех классов.
Обратимся, к экспериментальному классу школы №3 г. Тулы. В нем есть большая группа учеников, значительно продвинутых в общем развитии. Однако есть и очень слабые ученики.
В первый год обучения класс работал по программе, утвержденной Министерством просвещения РСФСР, но под руководством и по методическим указаниям лаборатории проблем обучения и развития учащихся. Учительница работала ранее в экспериментальном классе лаборатории.
Количественные результаты анализа работ в этом классе представлены в таблице 36.
Для индивидуальных бесед были выделены учителем 18 школьников (6 сильных, 6 средних и 6 слабых по успеваемости).
Анализ ответов этих учеников дал по полноте обоснования следующие результаты (табл. 37).
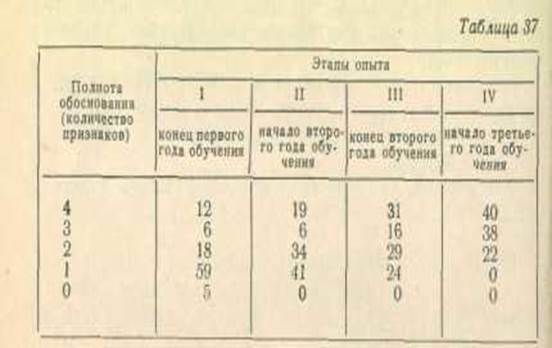
Данные о широте охвата признаков представлены в таблице 38.
Сопоставление таблиц 36, 37, 38 позволяет сказать, что процесс усвоения понятия «задача» протекает у учеников этого класса очень интенсивно и уже к концу второго года обучения подавляющее большинство их поднимаются на самые высокие ступени овладения этим понятием.
Для проверки упомянутого заключения классу было предложено дополнительное задание, которое содержало одну неарифметическую задачу: «Сколько всего квадратов изображено на этом чертеже?» (рис. 7). Ребятам было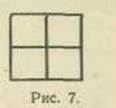 
предложено установить, задача это или не задача, и обосновать свой ответ. 78% всех опрошенных учеников (18 человек) дали правильный ответ: «Это задача». Все эти ученики верно нашли в ней условие, что представляло значительную трудность, так как оно выражено не в словесной форме, а с помощью чертежа.
Перейдем к экспериментальному классу школы № 2 г. Шатуры Московской области. Класс средний, много слабых учеников. С первого дня учительница работала по программам, учебникам и методическим указаниям лаборатории проблем обучения и развития. Учительница и раньше работала с лабораторией.
Результаты этого класса по всем трем линиям анализа представлены в таблицах.
Сопоставление данных, представленных в таблицах 36а, 36б, З6в, дает основание для следующих выводов: на первом этапе класс стоял на низком уровне усвоения понятия и первый год работы не дал ощутимых результатов. По всем линиям анализа показатели повысились лишь незначительно. Однако к третьему этапу произошел скачок, а к четвертому этапу класс показал чрезвычайно высокие результаты: 84% всех работ выполнены безошибочно.
Рассмотрим, какой путь прошли ученики обычного класса школы № 589 Москвы (см. табл. 37а, б, в).
Класс средний, работал под руководством учительницы с большим педагогическим стажем.
Сравним результаты, полученные в этих трех классах. В них есть некоторые общие черты. На первом году обучения во всех трех классах количество правильно выполненных работ невелико. Ко второму этапу результаты во всех классах улучшаются. Особенно это относится к экспериментальному классу тульской школы, а также обычному классу московской школы.
Наглядное представление о результатах выполнения работ дают графики на рисунке 8.
Графики показывают изменение числа правильно выполненных работ в двух из исследуемых классов, наиболее близких по исходным данным.
Как видим, начиная с конца второго года обучения результаты в экспериментальном и обычном классах; резко различны: если в экспериментальном классе количество правильно выполненных работ постоянно возрастает, то в обычном классе происходят резкие колебания от этапа к этапу при общей тенденции к снижению. результатов. Так, количество правильно выполненных работ в конце второго года обучения оказывается меньше, чем в конце первого года.
Сравним результаты первого и четвертого этапов в обычном и в каждом экспериментальном классе. На первом этапе число верно выполненных работ в тульском экспериментальном классе было в 2,5 раза выше, чем в обычном, а на четвертом этапе их становится уже в 5 раз больше. Но особенно разительные результаты даетсравнение с шатурским экспериментальным классом: на первом этапе правильно выполненных работ в этом классе было почти в 2 раза меньше, чем в обычном, а на четвертом этапе их стало в 6,5 раз больше.
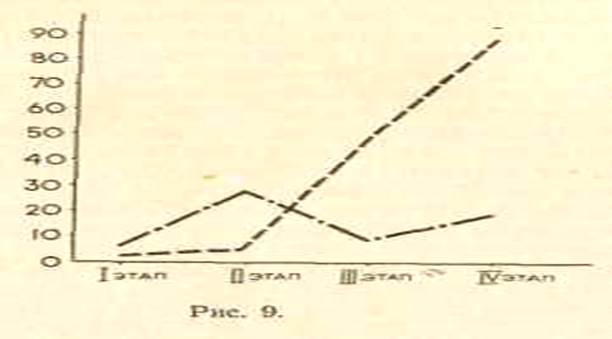
Серьезное внимание привлекает вопрос о характере ошибок, допущенных учениками. Анализ работ школьников I класса показал, что наибольшие затруднения вызвал текст, не имеющий искомого. Это естественно, так как данный текст по своей внешней конструкции неотличим от задачи. Дети же на этом этапе в основной своей массе опираются на формальное, внешнее сходство с задачами, которые они решали в классе.
Исходя из этого, можно предположить, что уменьшение количества ошибок в текстах, не имеющих искомого, говорит о более глубоком овладении материалом. На рис. 9 (см. с. 322) представлены графики, отражающие число учеников, правильно ответивших на вопрос о таких текстах.
Изменения, происходящие при выполнении этой части заданий, аналогичны общей тенденции изменений, происходящих при выполнении заданий полностью. Это позволяет предположить, что основой их является все более глубокое проникновение в смысл явления, а следовательно, и все более полное усвоение.
Перейдем к сравнению изменений, происшедших в качественных показателях.
И в одном и другом экспериментальном классе происходит непрерывное нарастание количества полных ответов, хотя нарастает оно по-разному.
Так, в тульском классе этот процесс протекает плавно, без заметных скачков. Что же касается шатурского класса, то на начальных этапах исследования наблюдается замедленное развитие процесса, а затем, от II к IIIклассу, происходит резкий скачок, и этот класс в дальнейшем идет впереди класса из школы г. Тулы.
Что касается обычного класса, то и на третьем году обучения не было получено ни одного ответа, опирающегося на все основные признаки, и только в 16% ответов были использованы 3 признака.
Обратимся к сравнению последнего показателя усвоения понятия «задача» – к широте охвата признаков.
Все оказанное выше говорит о том, что наблюдается резкое отставание учеников обычного класса от учеников экспериментальных классов и, чем больший срок проходит от начала знакомства с задачами, тем больше становится разрыв. Если школьники экспериментальных классов за два года обучения в подавляющем большинстве овладели данным понятием, то ученики обычного класса за этот же срок не продвинулись или почти совсем не продвинулись в овладении понятием «задача».
Поскольку ни в обычном, ни в экспериментальных классах учителя никакой специальной работы по отработке понятия «задача» не проводили, остается допустить, что различные результаты, к которым пришли ученики этих классов, следует отнести за счет глубокого своеобразия экспериментальной дидактической системы по сравнению с традиционной методикой.
В начале III четверти 1973/74 учебного года исследование было продолжено в восьми классах (4 – экспериментальных и 4 – обычных ). Его предметом стало составление задач школьниками вторых экспериментальных и обычных классов, а также решение составленных ими задач. Изучение осуществлено в виде письменных работ, которые проводились на 4 уровнях, следовавших друг за другом в порядке снижения требований, предъявляемых к школьникам. Формулировки заданий следующие.
/ уровень. «Даны числа: 48; 3; 12. Подумай и запиши задачу об игрушках так, чтобы она решалась в три действия и чтобы для ее решения нужно было использовать только данные числа в том порядке, в каком они записаны». Таким образом, при составлении задачи ученики должны были выполнить четыре условия: 1) выдержать заданную фабулу и 2) количество действий, 3) использовать только данные числа, 4) использовать их в предписанном порядке.
// уровень отличался от I тем, что снято было требование сохранения порядка использования чисел. Все остальные требования сохранялись.
/// уровень. Было снято требование о количестве действий. Остальные требования сохранялись, в том числе и требование о порядке использования чисел.
IV уровень. Были сняты два требования: о количестве действий, о порядке использования чисел.
После того как ученики составили задачу, им предлагалось ее решить.
Работа выполнялась в классе в учебные часы. Ученики сидели по одному за партой, поэтому состав класса делился на две группы и на работу уходило 2 урока. Задание было записано на доске. Помимо этого экспериментатор давал дополнительные разъяснения; обращал внимание детей на все требования к задаче, пояснял, что нужно записать задачу подробно, а не кратко (т. е. дать ее полный текст, а не краткую схему).
Собранные работы экспериментатор проверял и на другой день давал работу на более низком уровне тем, кто не справился с предыдущим.
Всего работу писали 244 ученика: 122 школьника экспериментальных классов и 122 – обычных классов.
На I уровне верно составили задачу в экспериментальных классах 55 учеников, что составило 45% всех учащихся, выполнявших работу, а в обычных классах – 12 учеников, или 10% всех учащихся. Из них верно решили составленные задачи в экспериментальных классах 49 учеников, или 89% всех школьников, справившихся с первой частью работы. В обычных классах верно решили свои задачи 9 учеников, или 75% всех справившихся на этом уровне с первой частью задания.
Привлекает внимание значительный перевес экспериментальных классов над обычными по количеству школьников, правильно составивших задачу на наиболее сложном уровне требований, предъявляемых к учащимся. Соответственно на последующих, все более простых уровнях упомянутое различие сначала нивелируется (на II уровне – 32% и 26%), а далее соотношение становится обратным (III уровень – 13% и 30%; IV уровень – 7% и 11%). Совсем не сумели составить задачу 3% учеников экспериментальных классов и 27% – обычных.
Различия между учениками экспериментальных и обычных классов ясно выступают в характере ошибок, допущенных при составлении задач. Подавляющее большинство (84%) ошибок в экспериментальных классах представляет собой несоблюдение отдельных требований (количество действий, порядок использования чисел), а также пропуски и неточности в текстах задач. Пример: «Было 48 машинок легковых, а грузовых на 3 больше, а хлебных на 21 меньше. Сколько машинок было всего?» Ход рассуждения верный, выдержаны все четыре требования, однако пропущены слова, точно определяющие пары сравниваемых величин («..чем легковых»; «...чем грузовых»). В случаях несоблюдения отдельных требований ход рассуждения также верен.
Следующие ошибки характерны для учеников обычных классов: 1) «В магазине было 48 мячей – в 3 раза больше, чем кукол, а кукол было 21 штука. Сколько всего игрушек в магазине?» 2) «В магазине всего 48 игрушек. Из них 21 кукла и 3 машины. Сколько изготовят машин за один месяц?»
Наиболее отчетливо прогресс, достигнутый школьниками экспериментальных классов, отображен в фактических данных, касающихся составления задач при предъявлении требований I уровня. Уже само по себе количественное соотношение школьников экспериментальных и обычных классов, правильно составивших задачи, свидетельствует о том, что первые выдерживают в комплексе все четыре требования. Следовательно, структура задачи для школьников экспериментальных классов ясна. Более того, их деятельность идет в строго определенном русле, не отклоняясь от него.
Ученики экспериментальных классов, которые не входят в приведенную нами цифру (45%), допустили ошибки при составлении задачи. Однако, как об этом сказано выше, большинство ошибок заключается в неточностях и несоблюдении отдельных требований.
По добытым фактам можно судить о процессе составления задач. Правильное составление задачи, особенно на I уровне, означает наличие в сознании школьника схемы ее решения. Эта схема должна быть «вывернута наизнанку», чтобы в результате ученик мог прийти к тексту составленной задачи.
Отмеченные качества школьников экспериментальных классов, как правило, отсутствуют у учеников классов обычных. Об этом ясно говорят и количественные данные (10%) верно составленных задач на I уровне, и характер допущенных ошибок (см. выше). Антиципация (предвосхищение) задачи, которая должна быть составлена, отсутствует. Вместо рассуждения здесь – применение закрепившихся в сознании штампов (если 48, а затем 3, то мячей в 3 раза больше, чем кукол). Осмысленные связи между частями текста задачи отсутствуют: вслед за утверждением, что мячей в 3 раза больше, чем кукол (а мячей – 48), говорится, что «кукол было 21 штука». Но если уже. известно, что кукол – 21, то зачем нужно предложение, что 48 мячей в 3 раза больше, чем количество кукол? И дальше – штамп: если в магазине разные игрушки, надо поставить вопрос: «Сколько всего игрушек в магазине?»
Подтверждением проведенного анализа составления задач школьниками экспериментальных и обычных классов служит сопоставление количества учеников, решивших ими же составленные задачи. Почти все школьники экспериментальных классов (90%) правильно решают ими же составленные задачи, а в обычных классах – лишь половина учеников (53%).
Итак, у школьников экспериментальных классов составление задачи представляет собой четкую структуру, где накопленный ими опыт решения задач гибок и податлив, адекватен выполнению нового задания. У учеников обычных классов составление задачи представляет собой механическое соединение закрепившихся в сознании элементов, и это соединение не соответствует выполнению предложенного задания.
Глава XVI
ЗНАНИЯ О ПРИРОДЕ
Овладение понятиями, умение отделить существенное в понятии от несущественного, умение соотнести понятия между собой должно способствовать лучшему пониманию закономерностей и зависимостей в окружающем мире.
Понятия как итог научного исследования раскрывают и обобщают существенные признаки вещей и явлений.
Вопрос о том, как происходит усвоение естествоведческих знаний школьниками начальных классов, какими понятиями и представлениями они владеют, рассматривался как в педагогической, так и в психологической литературе (М. Н. Скаткин, В. А. Горбачева, Э. И. Зал-кинд, Т. В. Косма, А. В. Скрипченко, П. Р. Чамата, М. С. Петербургская, М. К. Пискунова, А. Ф. Герасименко, Е. М. Кудрявцева, П. А. Завитаев, А. М. Низова, Л. И. Грехова и др.).
Наше исследование, представленное в данной главе, состоит из двух частей. Первая посвящена выявлению и пониманию школьниками некоторых взаимосвязей в природе, вторая – оперированию перекрещивающихся понятий.
Перейдем к первой части исследования. Чтобы вскрыть, как школьники обнаруживают связь между особенностями строения животных и их образом жизни, мы использовали следующую методику. Детям в индивидуальной беседе давалось для рассматривания цветное изображение орла-белохвоста на однотонном фоне, без пейзажа. Изучение этой птицы не входит в учебную программу, так что вероятность знакомства с ней очень мала. Задача опыта заключалась в выяснении того, насколько дети умеют при рассмотрении объекта выделять характерные особенности его внешнего вида и на этом основании делать заключение об образе жизни данного животного.
Мы предлагали школьникам три варианта вопросов, которые отличались друг от друга по степени сложности. Вопросы I варианта содержали лишь общее руководство к действию, II вариант определял направление анализа, а III вариант содержал готовую схему рассмотрения. Варианты предъявлялись детям в последовательном порядке. Сначала предлагался I вариант. Если ребенок испытывал затруднение, ему задавались по мере надобности дополнительные вопросы, соответственно по II либо III вариантам.
Ниже приводим упомянутые варианты.
/ вариант. Рассмотри внимательно эту птицу и сделай заключение о ее образе жизни.
// вариант. Рассмотри внимательно эту птицу.
1.Опиши ее внешнее строение и на основании его сделай заклю
чение о том, чем питается эта птица, где живет.
2.Почему так думаешь?
/// вариант. Рассмотри внимательно эту птицу и сделай заключение о ее образе жизни.
1. Рассмотри, какого она цвета, какое строение имеет голова,
клюв, ноги, какова величина и форма тела.
2.Как ты думаешь, чем она должна питаться (мясом других жи
вотных, зерном, насекомыми)? Какие признаки на это указывают?
3.Где она должна жить? Каюие признаки на это указывают?
Наши опыты проводились в I, II и III экспериментальных классах школ № 3, 125, 544 Москвы и школы № 2 г. Шатуры Московской области, в I, II и III обычных классах школ № 144, 589, 683 Москвы.
Из каждого класса мы брали группу учеников, в которую входили разные по успеваемости дети (сильные, средние, слабые). Всего в наших опытах участвовало 114 учеников экспериментальных классов (по 38 учеников из каждой параллели) и столько же (114) учеников обычных классов.
Материал, полученный в результате исследования, позволил выявить некоторые особенности в нахождении взаимосвязей школьниками, обучающимися по разным педагогическим системам.
Чтобы пояснить, как проходили опыты, приведем некоторые протоколы.
Ученику экспериментального класса Мише Д. (средний по успеваемости школьник) дается изображение птицы. Ученик Миша Д
Сопоставим количественные данные, полученные в экспериментальных и обычных классах на первом, втором и третьем годах обучения. Одним из показателей усвоения школьниками данного материала является понимание ими вопроса экспериментатора. В таблице 39 мы приводим количество школьников, которые смогли понять задание при предъявлении им разных вариантов вопросов
Таблица 39
Количественные данные, приведенные в данной таблице, показывают, что большинство учеников экспериментальных классов приступают к ответу при.предъявлении I или II варианта вопросов. Притом количество учеников, справившихся с заданием при предъявлении им
I варианта вопросов, увеличилось от 3 человек в первых классах до 28 человек в третьих. Руководствуясь этим вариантом, дети не только смогли детально рассмотреть изображение птицы, но и легко установили связь между ее внешним строением и образом жизни.
Количество учеников, которые смогли приступить к выполнению задания только после предъявления им III варианта вопросов, сократилось от 10 учеников в первых классах до 3 человек во вторых, а в третьих классах ни одному ученику не понадобилось давать вариант, содержащий полную схему анализа.
Данные, полученные в обычных классах, показывают, что большинству учеников необходимо предъявить II и III варианты, чтобы они смогли понять задание и приступить к его выполнению. Количество учеников, приступивших к выполнению задания лишь после того, как экспериментатор задал им вопросы III варианта, в этих классах остается еще очень большим. Ученики обычных классов не могут понять, а следовательно, и выполнить задание при его формулировании в общем виде. Необходим ряд конкретных вопросов, раскрывающих ход выполнения задания.
Возможность выявления связи между внешним строением животного, средой обитания и питанием требует довольно тонкого анализа предъявленного объекта. Ученики должны выделить существенные особенности строения тела птицы и, основываясь на них, сделать заключение о том, где она живет и чем питается.
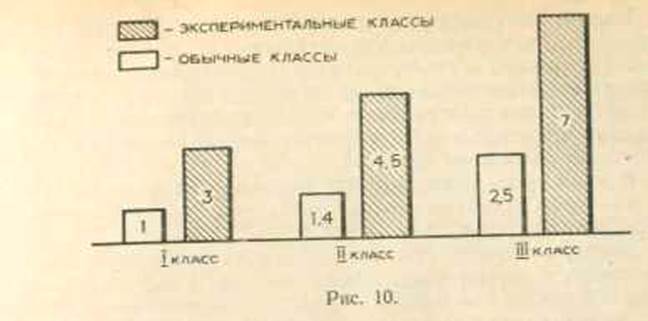
Анализ данных, полученных в индивидуальных беседах с детьми, показал, что ученики экспериментальных классов подмечают значительно больше важных свойств строения тела животного, чем ученики обычных классов. Количество существенных особенностей птицы (среднее арифметическое) представлено на рисунке 10.
Результаты, полученные в этом исследовании, позволяют сделать вывод, что ученики экспериментальных классов полученные знания могут переосмыслить и применить в нужной ситуации. Школьники ориентируются в
предъявленном материале, вскрывают существенные взаимосвязи.
Очень важно, что школьники экспериментальных классов свободно оперируют предъявленным материалом. Об этом свидетельствует, во-первых, характер высказываний учащихся, большое разнообразие суждений, отсутствие схем и, во-вторых, обнаруженная у школьников третьих экспериментальных классов возможность руководствоваться вопросом в общем виде. Такой вопрос давал большую свободу как для выявления связей, так и для их обоснования и доказательства.
Вторая часть нашего исследования была проведена в начале III четверти 1973/74 учебного года.
Выполнение заданий, предложенных школьникам, осложнялось тем, что содержанием являлись. перекрещивающиеся понятия. Задания такого вида позволяли глубже познать овладение естествоведческими знаниями в сравнительном плане – при разных системах обучения.
Исследование проведено в семи вторых классах: трех экспериментальных и четырех обычных. Экспериментальные классы были взяты в школе № 43 г. Рыбинска (учительницы С. А. Гусева и А. Д. Иванова) и один класс в школе № 2 г. Шатуры (учительница И. С. Стрижевская), обычные классы – в школе № 54 Москвы (два класса) и в школе № 345 Москвы (два класса).
Изучение осуществлялось путем письменной работы и индивидуальных бесед.
Работа включала названия животных, при систематизации которых должны учитываться следующие понятия: «домашнее животное», «дикое животное», «хищное животное», «травоядное животное».
За 2–3 дня до письменной работы проводился индивидуальный опрос учеников для выявления их знакомства с упомянутыми понятиями.
В день проведения работы на доске были написаны 10 названий животных: лось, слон, лев, кошка, коза, волк, лошадь, овца, лиса, собака.
Экспериментатор громко, четко читает названия этих животных и спрашивает, все ли животные знакомы ученикам. Если то или иное животное не знакомо кому-либо из учеников, давались соответствующие разъяснения.
Затем следовала инструкция для выполнения работы. Экспериментатор говорит, что надо разделить названия данных животных на 4 группы, так, чтобы каждое название входило только в одну группу. Школьникам предлагается внимательно прочитать названия животных, хорошенько подумать и решить, по каким признакам разделить данных животных на 4, и только на 4, группы. Дается указание, что на листочках надо расположить группы I и II в верхней части листа, а III и IV – под ними.
Как показало поведение школьников, инструкция была вполне им понятна.
Предложенное задание можно выполнить правильно при условии, если отнесение каждого животного к той или иной группе проводится с учетом двух признаков одновременно: 1) с точки зрения одомашнения и 2) с точки
|
|
|
