 |
Потоки событий. Простейший поток.
|
|
|
|
События, образующие поток, в общем случае могут быть различными, но мы будем рассматривать лишь поток однородных событий, различающихся только моментами появления. Такойпоток можно изобразить как последовательность точек t1, t2 , …, tк нa числовой оси (оси времени).
0 t1 t2 t3 t
События, образующие поток, сами по себе вероятностью не обладают: вероятностью обладают другие, производные от них события, например, такое: "на участок времени t попадают ровно два события".
Интенсивность потока - среднее число событий, приходящихся на единицу времени. Обозначение: λ.
Интенсивность потока может быть как постоянной (λ = const), так и переменной, зависящей от времени t. Поток событий называется стационарным, если вероятность появления того или иного числа событий за некоторое время t зависит только от величины t и не зависит от того; где на оси ot расположен этот отрезок времени. Вероятностные характеристики таких потоков не зависят от времени, в частности, интенсивность λ = const.
Поток событий называется потоком без последствия, если вероятность появления какого-либо числа событий в данный отрезок времени не зависит от того, сколько событий появилось в другие отрезки времени, не пересекающиеся с данным.
Поток событий называется ординарным, если вероятность появления двух или нескольких событий в малый отрезок времени мала по сравнению с вероятностью появления одного события, то есть события в потоке появляются практически по одному.
Потоки, являющиеся одновременно потоками стационарными, без последствий и ординарными, называются простейшими или стационарными пуассоновскими [9].
Если поток событий простейший, то вероятность Р т (t) того, что на любой интервал времени t попадёт т событий, определяется формулой:
|
|
|
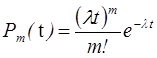, где λ≥0 и равно интенсивности потока.
Пример 28. Поток донесений, поступающих вштаб, внекоторых условиях практически является простейшим с интенсивностью λ=0,8 донесение в час. Найти вероятность того, что в течение 5 часов:
1) не поступит ни одного донесения;
2) поступит два донесения;
3) поступят, по крайней мере, два донесений.
Решение.
Исходные данные: λ=0,8; t =5. Требуется определить:P0, P2 и Р т ≥ 2.
По формуле (1) найдём:
;
;
.
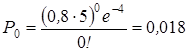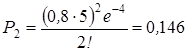Рт≥ 2=1-(Р 0+ Р 1)=1-(0,018+0,058)=0,924.
В подавляющем большинстве случаев, особенно в задачах прикладного характера, в теории массового обслуживания рассматриваются простейшие потоки. В дальнейшем, говоря о потоке событий, мы будем подразумевать простейший поток.
Граф состоянии. Размеченный граф состояний
При анализе случайных процессов с дискретными состояниями удобно пользоваться геометрической схемой - так называемым графом состояний: состояние системы изображается прямоугольником, в котором записаны обозначения состояний S1, S2, S3,,..., а возможные переходы из состояния в состояние - стрелками.
 |
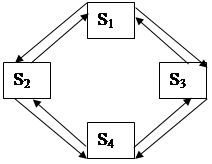Построим, например, граф состояний системы S, описанной в примере 27 пункта 3.1.2 (рисунок 16).
Рисунок 16
Стрелка, направленная из S1 в S2, означает переход в момент отказа первого узла.
Стрелка, направленная обратно из S2 в S1 - переход в момент окончания ремонта первого узла.
Остальные стрелки объясняются аналогично.
Предполагается, что узлы выходит из строя независимо друг oт друга, т.е. вероятность одновременного выхода двух узлов мала и ею пренебрегают. (Стрелка, ведущая из S1 в S4, отсутствует).
Пусть имеется некоторая система S с состояниями Sk (к =I,2,3,..., п), и переход системы из состояния S i в состояние S j происходит под действием простейших потоков событий (поток вызовов, поток отказов и т.д.). Итак, в системе происходит марковский процесс.
|
|
|
Обозначим λ i j - интенсивности потока событий, переводящих систему S из состояния S i в состояние S j.
 |
Проставим интенсивности потоков событий на графе состоянии. Получим так называемый размеченный граф состояний.
Рисунок 17
На рисунке 17 показан размеченный граф состояний для системы S с тремя состояниями S1, S2, S3.
Из состояния S1 в состояние S 2система переходит под действием простейшего потока событий интенсивностью λ12из S2 в S1 под действием потока событий интенсивностью λ21 и т.д.
Пример 29. Построим размеченный граф состояний для системы S примера 27 (пункт 3.1.2)
Напомним состояние системы:
S1 - оба узла исправны;
S 2- первый узелремонтируется, второй исправный;
S 3- второй узел ремонтируется, первый исправный;
S4- оба узла ремонтируются.
Граф состояний этой системы мы уже построили (см. рис. 17)
Пусть t1 и t2 — среднее время безотказной работы первого и второго узлов соответственно.
T1 и Т2 - среднее время ремонта первого и второго узлов.
Интенсивность потоков событий, переводящих систему из состояния в состояние, будем вычислять, предполагая, что среднее время ремонта не зависит от того, ремонтируется ли один узел или оба сразу (это будет именно так, если ремонтом каждого узла будет занят отдельный специалист).
 |
Найдем интенсивность всех потоков событий, переводящих систему из состояния в состояние.
S1- S2 - Этот переход совершается под действием потока отказов первого узла
 |
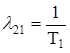S2 - S1 - Этот период совершается под действием потока окончания ремонта первого узла
S1 - S3 - поток отказов второго узла
 |
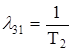S3 - S1 - поток окончания ремонта второго узла
S 2- S4- поток отказов второго узла 
,
S4 - S2 - поток окончания ремонта второго узла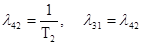 
S 3- S4- поток отказов второго узла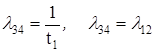 
,
S4 - S3 - поток окончания ремонта первого узла 
На рисунке 18 получили размеченный граф состояний системы S.
Имея в своём распоряжении размеченный граф состояний системы, легко построить математическую модель системы.
Уравнения Колмогорова длявероятностей состояния
Пусть рассматривается система S, имеющая п возможных состояний S1, S2, S3,...S п.
Вероятностью i - го состояния называется вероятность того, чтов момент t система будет находится в состоянии S i.
|
|
|
Обозначим: P i (t).
Для любого момента времени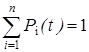 
.
Имея в своём распоряжении размеченный граф состояний, можно найти все вероятности P i (t) как функции от времени. Для этого составляются и решаются уравнения Колмогорова - особого вида дифференциальные уравнения, в которых неизвестными функциями являются вероятности состояний [5].
Составим, например, уравнение Колмогорова для системы, размеченный граф состояний которой приведён на рисунке 19.
 |
Рисунок 19
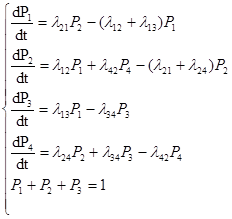(24)
Сформулируем общее правило составления уравнений Колмогорова.
Производная вероятности каждого i -го состояния системы равна сумме произведений вероятностей всех состояний, из которых идут стрелки в данное (i -е) состояние, на интенсивности соответствующих потоков минус произведение вероятности i -го состояния на суммарную интенсивность всех потоков, выводящих систему из данного состояния.
Составим уравнение Колмогорова для системы S, размеченный граф состояний которой приведён на рисунке 18, (система; состоящая из двух узлов, см. пункт 3.1.2.)
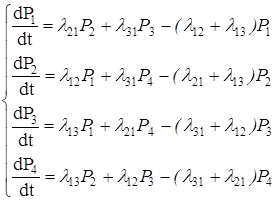. (25)
Чтобы решить уравнения Колмогорова и найти вероятности
состояний, надо задать начальные условия.
Например, уравнения (25) естественно решить при начальных условиях Р1(0)=1, Р2 (0)=Р3 (0)=Р4(0)=0 (т.е. считаем, что в начальный момент оба узла исправны).
Заметим, что одно из уравнений системы (любое) можно всегда отбросить, учитывая, что P1+P2+....+ Р п = 1.
Как решать уравнения Колмогорова?
Если число уравнений невелико (не более трёх), то их можно решать аналитически, как нормальную систему дифференциальных уравнений; при большем количестве уравнений систему решают с помощью ЭВМ. Решение этих уравнений даёт возможность найти вероятности состояний системы как функции от времени.
|
|
|
