Порядок розрахунків. Контрольні запитання.. Лабораторна робота № 3.2 „Вивчення методів вимірювання опору та визначення температури нитки лампи розжарювання”.

Порядок розрахунків.

1. Побудувати графічну залежності lnІ ( t ) за даними вимірювань та зробити висновки про характер розряду конденсатора через резистор.

2. Знайти середнє значення часу t ¢ з трьох вимірювань для кожного з конденсаторів (пункти 9 і 10).

3. Розрахувати за даними середніх значень t ¢ за допомогою формули (3. 60) ємності конденсаторів < С₁ >, < C₂ >, < C_пар >, < C_пос >.

4. Розрахувати теоретичні значення ємностей паралельно C ¢ і послідовно C ¢ ¢ з’єднаних конденсаторів за формулами:

          ,                                                             (3. 61)

                                                                          (3. 62)

та порівняти їх з раніш розрахованими < C_пар >, < C_пос >:

       ,                                                    (3. 63) 

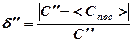       .                                                   (3. 64)

5. Розрахувати середньоквадратичні похибки вимірювання ємностей:

        ,                                                         (3. 65)

де 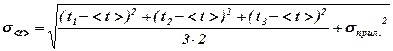                     (3. 66)

Контрольні запитання.

1. Сформулюйте закон збереження електричного заряду.

2. В чому полягає закон Кулона? Для яких зарядів він справедливий?

3. Що таке електричне поле? Назвіть його характеристики. Сформулюйте принцип суперпозиції.

4. Охарактеризуйте поведінку провідника в електричному полі. Що називають електроємністю ізольованого провідника? Від чого вона залежить?

5. Що розуміють під конденсатором? Визначте електроємність конденсатора. Які бувають конденсатори за формою обкладинок та як обчислюється їх електроємність?

6. Які бувають види з’єднань конденсаторів та які властивості напруги, заряду, електроємності при цих з’єднаннях?

7. Сформулюйте методику визначення ємності конденсатора в даній роботі.

8. Що також перевіряється в роботі?

 

Лабораторна робота № 3. 2 „Вивчення методів вимірювання опору та визначення температури нитки лампи розжарювання”.

Мета роботи: Ознайомлення з існуючими методами вимірювання опору, визначення температури розжареної нитки лампи за відомим значенням температурного коефіцієнта опору її нитки.

Існують різні методи вимірювання опору, з яких ми розглянемо і будемо використовувати в даній лабораторній роботі ось такі: мостовий (а) та амперметра і вольтметра(б).

а. Мостова схема постійного струму (рис. 3. 5) являє собою замкнений чотирикутник, побудований на опорах R_x, R₁, R₂, R₃ та з’єднаних між собою провідниками. В одну з діагоналей цієї схеми вмикають джерело струму, а в іншу – чутливий гальванометр (амперметр для вимірювання дуже малих струмів). Саме ця діагональ має назву моста.

При довільних значеннях опорів струм через гальванометр тече. Однак, при двох фіксованих значеннях опорів R₂ і R₃ завжди можна підібрати таке співвідношення між опорами R_x і R₁, щоб струм в гальванометрі був відсутній. Відсутність струму означає, що потенціали точок С та Д однакові.      

Нехай I₁, I₂, I₃, I₄ –сили струмів в плечах моста R_x, R₁, R₂, R₃. Коли струм через гальванометр дорівнює нулю, то в точках С та Д немає розгалуження струмів і тому I₁ = I₂, I₃ = I₄. Напруги між кінцями плечей моста дорівнюють:

                                             (3. 67)

Оскільки напруга між точками С та Д дорівнює нулю, то U_AC = U_AД і тоді

 

 R_x I₁ = R₁ I₃ .                                                                             (3. 68)

Аналогічно, U_СВ = U_ВД і тоді

                     R₂ I₂ = R₃ I₄                                                                  (3. 69)

Поділимо вираз (3. 68) на (3. 69), одержимо з урахуванням I₁ = I₂, I₃ = I₄ такий вираз:

           або                                               (3. 70)

б. Метод вольтметра і амперметра. Цей метод полягає в безпосередньому вимірюванні як величини струму, що протікає через опір, так і величини спаду напруги на опорі. При цьому можна записати згідно з законом Ома

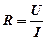                                                                                                   (3. 71)

Насправді, можливі дві схеми вимірювань напруги та сили струму (Рис. 3. 6 і 3. 7). В першій схемі амперметр вимірює силу струму через опір R, а вольтметр вимірює напругу на послідовно з’єднаних амперметрі та опорі.

Якщо опір амперметра R_a, то значення невідомого опору буде дорівнювати

                           (3. 72)

Очевидно, що у випадку R_a < < R другим доданком у дужках можна знехтувати і ми прийдемо до виразу (3. 71).

В другій схемі (рис. 3. 7) амперметр вимірює силу струму, що протікає через опір R, а вольтметр вимірює напругу на опорі.

В цьому випадку невідомий опір можна обчислити таким чином:

                             (3. 73)

Тут R_V – опір вольтметра. У випадку дуже великого значення опору вольтметра, тобто R_V > > R, другим доданком у дужках можна знехтувати, і ми знову ж таки прийдемо до виразу (3. 71).

Визначення температури розжареної нитки лампи розжарювання.

Як було вказано раніше, для не дуже великих температур опір металевих провідників залежить від температури за лінійним законом

                 .                                                         (3. 74)

Тут R₀ – опір провідника при температурі 0^оС. Застосуємо цю формулу для кімнатної температури t_к: , звідки 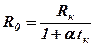. Виразимо температуру з формули (3. 74) і підставимо в неї опір R₀ з останнього виразу. Одержимо тоді:

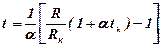                                                                 (3. 75)

Опір холодної нитки визначається мостовим способом. При цьому припускаємо, що величина струму, що протікає через нитку, дуже мала, і тому температура холодної нитки дорівнює температурі навколишнього середовища.

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: