 |
Контрольні запитання. Модуль 2. 3. Електрика.. 3.1. Електростатика.
|
|
|
|
Контрольні запитання.
Відповіді на контрольні запитання можна занести у протокол лабораторної роботи у Теоретичному вступі.
1. Що називають вектором кутового переміщення точки?
2. Як визначається вектор кутової швидкості? Як вона зв’язана з вектором лінійної швидкості?
3. Як знайти величину і напрямок тангенціального та нормального прискорень?
4. Що називають вектором кутового прискорення? З яким лінійним прискоренням зв’язане кутове прискорення?
5. Як визначаються момент імпульсу матеріальної точки відносно точки та осі обертання?
6. Що називають моментом інерції матеріальної точки? Який фізичний зміст цієї величини?
7. Дайте визначення моменту сили матеріальної точки відносно точки та осі обертання?
8. Запишіть основний закон динаміки (другий закон Ньютона) для обертального руху двома способами.
9. Як визначається кінетична енергія при обертальному русі?
10. Що називають абсолютно твердим тілом? Чому при розгляданні його обертального руху використовують кутові характеристики руху?
11. Як визначити момент інерції системи матеріальних точок та твердого тіла? Сформулюйте теорему Штейнера.
12. Що називають фізичним маятником? Запишіть диференціальне та інтегральне рівняння коливального руху маятника. За якою формулою обчислюється період коливань фізичного маятника?
13. Які складові вимірювальної установки? Що треба вимірювати в роботі безпосередньо і що розраховувати?
14. Як за допомогою теореми Штейнера записати вираз для моменту інерції довгого тонкого стержня у випадку, коли вісь обертання проходить крізь кінець стержня.
Модуль 2
3. Електрика.
3. 1. Електростатика.
|
|
|
В електростатиці вивчаються властивості і взаємодія нерухомих електричних зарядів. Носіями заряду є елементарні частинки, такі як електрони та протони. В природі існують два види електричних зарядів: позитивний та негативний. Існує у вільному стані найменший заряд – елементарний, значення якого дорівнює е = 1. 6× 10-19 Кл. Величина будь – якого заряду дорівнює цілому числу N елементарних зарядів, тобто можна записати: q = N e.
Заряди можуть виникати і зникати, але завжди парами. Таким чином, є справедливим закон збереження електричного заряду: сумарний заряд ізольованої системи залишається сталим. Дляопису заряджених тіл будемо користуватися декількома моделями, найпростіша з яких – точковий заряд. Поняття про точковий заряд аналогічне поняттю матеріальної точки в механіці. Точковий заряд – це заряджене тіло, розмірами якого можна знехтувати у порівнянні з відстанями від цього зарядженого тіла до інших заряджених тіл. Для точкових зарядів є справедливим закон Кулона: сила взаємодії двох точкових зарядів прямо пропорційна величині кожного з зарядів та обернено пропорційна квадрату відстані між ними. Напрям сили збігається з прямою, яка проходить через центри зарядів. Математичний запис цього закону:
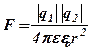. (3. 1)
де e - діелектрична проникність середовища,
e о = 8. 85× 10-12 Ф/м – електрична стала.
Взаємодія між нерухомими електричними зарядами здійснюється за допомогою електростатичного поля. Це форма існування матерії поряд з речовиною. Електростатичне поле виникає навколо будь – якого заряду, воно діє з деякою силою на інші заряди, які потрапляють в це поле.
Основна характеристика електростатичного поля – напруженість електростатичного поля. Напруженість електростатичного поля – це векторна фізична величина, яка дорівнює відношенню сили F, яка діє на позитивний пробний заряд qo, розташований в електричному полі, до величини цього пробного заряду.
|
|
|
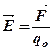(3. 2)
Розглянемо випадок точкового заряду. Легко довести, враховуючи закон Кулона та визначення напруженості поля, що напруженість поля точкового заряду визначається за формулою
(3. 3)
де q – величина точкового заряду,
r – відстань від точкового заряду до точки, де визначається напруженість поля.
Лінії напруженості електростатичного поля – це лінії, дотичні до яких збігаються з вектором напруженості в кожній точці поля. Ці лінії дозволяють легко зображати різні електростатичні поля. Важлива властивість цих ліній полягає в тому, що вони починаються на позитивних зарядах та закінчуються на негативних.
Для напруженості електростатичного поля є справедливим принцип суперпозиції. Він полягає в тому, що напруженість поля, утвореного довільною системою точкових зарядів, дорівнює векторній сумі напруженостей полів, які утворювали б в цій точці кожний заряд окремо.
Сили, які діють в електростатичному полі, є консервативними. Звідси випливає, що пробний заряд, який знаходиться в електростатичному полі, має потенціальну енергію. Згідно з загальним визначенням, потенціальна енергія пробного заряду, який знаходиться в деякій точці В поля, дорівнює роботі, що виконується силами поля по переміщенню пробного заряду з точки В в деяку фіксовану точку простору – точку відліку потенціальної енергії. Для систем зарядів в якості такої точки звичайно обирають нескінченно віддалену точку (∞ ). Таким чином, записуючи роботу по переміщенню заряду в електростатичному полі, враховуючи формулу (3. 2), маємо:
(3. 4)
Потенціальна енергія пробного заряду не може бути характеристикою поля, оскільки вона залежить від величини пробного заряду. Однак, згідно з (3. 4), ця залежність прямо пропорційна, тому відношення потенціальної енергії до величини пробного заряду вже не залежить від нього. Відношення потенціальної енергії пробного заряду, який знаходиться в деякій точці поля, до величини цього заряду називається потенціалом електростатичного поля в цій точці:
|
|
|
(3. 5)
З цього визначення випливає, що потенціал чисельно дорівнює потенціальній енергії одиничного позитивного заряду. Одиниця вимірювання потенціалу в системі СІ – вольт (В). 1В = 1 Дж /1 Кл.
Потенціал електростатичного поля – скалярна величина.
Виведемо формулу для потенціалу поля точкового заряду q. Потенціальну енергію пробного заряду, який знаходиться на відстані r від заряду q, знайдемо згідно з визначенням (3. 4). Для цього врахуємо формулу для напруженості поля точкового заряду (3. 3). Тоді одержимо:
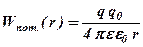. (3. 6)
Для потенціалу, як і для напруженості, виконується принцип суперпозиції, тобто потенціал в кожній точці поля, яке утворено системою зарядів, дорівнює сумі потенціалів полів, які утворювали б в цій точці заряди системи окремо:
. (3. 7)
Знаючи потенціал, можна обчислювати роботу, яка виконується силами поля при переміщенні пробного заряду з однієї точки простору В в іншу точку С:
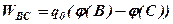(3. 8)
Таким чином, робота визначається різницею потенціалів в початковій та кінцевій точках шляху. З цієї формули випливає також фізичний зміст різниці потенціалів: вона чисельно дорівнює роботі сил електростатичного поля по переміщенню одиничного пробного заряду з початкової точки в кінцеву.
За своїми електричними властивостями усі тіла можна поділити на дві групи: провідники та діелектрики. Провідник в електростатиці – це тіло, в якому є багато вільних зарядів, тобто таких, які можуть вільно рухатись під дією сил електростатичного поля. В діелектриках таких вільних зарядів немає. Досліди приводять до наступного положення: якщо надати провіднику заряд або розташувати провідник в зовнішньому електростатичному полі (можна зробити обидві речі одночасно), то через малий проміжок часу (час релаксації) в провіднику встановиться рівноважний розподіл зарядів. Рівноважний розподіл зарядів на провідниках та їх електростатичне поле мають деякі властивості. Перш за все, оскільки після встановлення розподілу зарядів рух вільних зарядів в провіднику відсутній, то на ці заряди не діють сили. Отже, електростатичне поле всередині провідника відсутнє: Е = 0. Якщо провідник заряджений і зовнішнє поле відсутнє, то заряд розподіляється по провіднику так, що утворене ним поле відрізняється від нуля лише зовні провідника. Якщо ж нейтральний провідник розташований в зовнішньому електростатичному полі, то в ньому відбудеться перерозподіл зарядів (явище електростатичної індукції) таким чином, що поле індукованих зарядів компенсує зовнішнє поле всередині провідника. Далі, вектор напруженості на поверхні провідника перпендикулярний цій поверхні. В протилежному випадку, якщо б відрізнялись від нуля складові вектора напруженості уздовж поверхні провідника, то це приводило б до виникнення переміщення вільних зарядів уздовж поверхні. Оскільки поле всередині провідника відсутнє, робота по переміщенню пробного заряду всередині провідника дорівнює нулю, незалежно від положення початкової та кінцевої точок. Враховуючи, що ця робота пов’язана з різницею потенціалів (3. 8), робимо висновок, що потенціал усіх точок провідника однаковий. Існує зв’язок між поверхневою густиною заряду на поверхні провідника та напруженістю поля в цій самій точці:
|
|
|
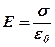(3. 9)
Розподіл зарядів суттєво залежить від форми поверхні провідника: поверхнева густина заряду максимальна на опуклих частинах поверхні з малим радіусом кривини і мала в западинах. Враховуючи формулу (3. 9), відповідним чином поводить себе поле.
Оскільки потенціал в усіх точках провідника однаковий, то можна говорити про потенціал провідника. Теорія та дослід вказують, що потенціал провідника j прямо пропорційний заряду провідника q:
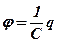(3. 10)
де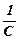 
- коефіцієнт пропорційності. Отже, відношення заряду до потенціалу є для даного провідника сталою величиною, яка називається електричною ємністю самотнього провідника:
(3. 11)
Ємність залежить від геометричних властивостей провідника – його розмірів та форми – та не залежить від матеріалу. Візьмемо приріст від обох частин формули (3. 11), одержимо:
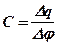(3. 12)
|
|
|
Звідси випливає фізичний зміст ємності: вона чисельно дорівнює заряду, який необхідно надати провіднику, щоб збільшити його потенціал на одиницю. Одиниця ємності в системі СІ носить назву “Фарад”: 1Ф=1Кл/1В.
Наприклад, для ємності ізольованої кулі, яка є провідником, можна одержати:
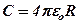(3. 13)
З цієї формули видно, що ємність в 1 фарад має куля радіуса 9× 109 м, що в 1500 разів більше, ніж радіус Землі. Тому на практиці користуються іншими одиницями – мікрофарадом (1 мкФ = 10-6 Ф) та пікофарадом (1 пФ = 10-12 Ф). Формула (3. 13) справедлива тільки для провідників сферичної форми, але її можна використовувати для якісних оцінок ємності несферичних тіл, розуміючи під R характерний розмір тіла.
В радіотехніці широко використовуються конденсатори – пристрої, які складаються з двох металевих обкладинок, розміри яких (наприклад, довжина пластини квадратної форми) суттєво більші, ніж відстані між ними. Якщо обкладинкам конденсатора надати заряди однакової абсолютної величини, але протилежного знаку, то електричне поле буде практично повністю зосереджене в просторі між обкладинками. В залежності від форми обкладинок розрізняють плоскі конденсатори (обкладинки – паралельні площини), циліндричні (обкладинки – коаксіальні циліндричні поверхні), сферичні (обкладинки – концентричні сфери).
Електричною ємністю конденсатора називають відношення величини заряду однієї з обкладинок до різниці потенціалів (напруги) між обкладинками:
(3. 14)
Наведемо формули, за якими можна обчислити ємності конденсаторів різних типів.
Для плоского конденсатора
, (3. 15)
де e - діелектрична проникність діелектрика, eо – електрична стала, S – площа кожної пластини, d - відстань між пластинами.
Для сферичного конденсатора
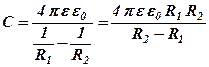, (3. 16)
де R1 та R2 – відповідно радіуси внутрішньої та зовнішньої сфер.
Для циліндричного конденсатора
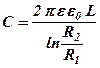, (3. 17)
де L – висота кожного з циліндрів, R1 та R2 – відповідно радіуси внутрішнього та зовнішнього циліндрів.
Конденсатори можна з’єднувати між собою, утворюючи батареї конденсаторів. Розглядають паралельне та послідовне з¢ єднання. При паралельному з’єднанні напруга на кожному конденсаторі однакова, заряд батареї конденсаторів дорівнює сумі зарядів на кожному конденсаторі, ємність батареї дорівнює сумі ємностей окремих конденсаторів, тобто:
, (3. 18)
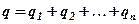, (3. 19)
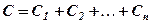(3. 20)
При послідовному з’єднанні заряди на усіх конденсаторах однакові, напруга батареї конденсаторів дорівнює сумі напруг на окремих конденсаторах, величина, обернена ємності батареї, дорівнює сумі обернених ємностей конденсаторів, тобто:
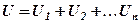, (3. 21)
, (3. 22)
(3. 23)
Комбінуючи конденсатори різними способами, можна змінювати ємність батареї конденсаторів в великих межах.
|
|
|
