 |
Контрольні запитання.. Лабораторна робота № 2.2 „Визначення моментів інерції тіл”.
|
|
|
|
Контрольні запитання.
Відповіді на контрольні запитання можна занести у протокол лабораторної роботи у Теоретичному вступі.
1. Що називають вектором кутового переміщення точки?
2. Як визначається вектор кутової швидкості? Як вона зв’язана з вектором лінійної швидкості?
3. Як знайти величину і напрямок тангенціального та нормального прискорень?
4. Що називають вектором кутового прискорення? З яким лінійним прискоренням зв’язане кутове прискорення?
5. Як визначаються момент імпульсу матеріальної точки відносно точки та осі обертання?
6. Що називають моментом інерції матеріальної точки? Який фізичний зміст цієї величини?
7. Дайте визначення моменту сили матеріальної точки відносно точки та осі обертання?
8. Запишіть основний закон динаміки (другий закон Ньютона) для обертального руху двома способами.
9. Як визначається кінетична енергія при обертальному русі?
10. Що називають абсолютно твердим тілом? Чому при розгляданні його обертального руху використовують кутові характеристики руху?
11. Як визначити момент інерції системи матеріальних точок та твердого тіла? Сформулюйте теорему Штейнера.
12. 
Які складові вимірювальної установки? Що треба вимірювати в роботі безпосередньо і що розраховувати?
13. Як в роботі перевіряють основний закон динаміки обертального руху, визначають момент інерції диска, момент сил тертя, підтверджують закон збереження енергії?
Лабораторна робота № 2. 2 „Визначення моментів інерції тіл”.
Мета роботи: вивчити коливальний процес на прикладі фізичного маятника, експериментально визначити його момент інерції, перевірити теорему Штейнера.
Теоретичні відомості та обґрунтування методики.
|
|
|
Під фізичним маятником розуміють будь - яке тверде тіло, здатне виконувати коливання навколо осі, яка не проходить через його центр мас.
Коливальний рух маятника можна розглядати як обертальний рух твердого тіла відносно осі, яка проходить через точку закріплення маятника перпендикулярно площині його коливань. Саме тому його рух можна описувати за допомогою рівняння динаміки обертального руху (2. 15), яке перепишемо з урахуванням визначення вектора кутового прискорення
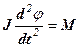(2. 2. 1)
де J – момент інерції маятника,
j - кут відхилення маятника від положення рівноваги,
M - момент сил, які діють на маятник (рис. 2. 9)
В даній роботі в якості фізичного маятника використовується однорідний стальний стержень довжиною ℓ . На кінці стержня закріплена опорна призма, гостре ребро якої є віссю котіння маятника. Таким чином відстань ОС = d від точки опори маятника до його центра мас дорівнює ℓ /2. Момент інерції довгого стержня відносно осі, що проходить через його центр мас, визначається як J0 = mℓ 2/12. Згідно з теоремою Штейнера (формула 2. 20) момент інерції цього ж стержня відносно осі, що проходить через його кінець, знайдемо так:
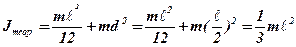(2. 2. 2)
Момент сили тяжіння, який діє на маятник,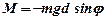 
. Якщо кут j малий, то sinj » j і тоді 
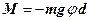. В установці маятник виконує декілька сотень коливань без помітного згасання. Тому моментом сили тертя в першому наближенні можна знехтувати. Підставляючи вираз для моменту сили в формулу (2. 2. 1), одержимо рівняння
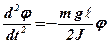(2. 2. 3)
З теорії диференціальних рівнянь відомо, що його розв’язанням є гармонічна функція φ = φ осоsω t, де 
- циклічна частота коливань. Вона зв’язана з періодом Т співвідношенням
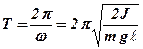(2. 2. 4)
|
|
|
Як випливає з співвідношення (9. 4), період коливань фізичного маятника визначаться його моментом інерції. Таким чином, визначаючи експериментально масу m , період коливань Т i довжину стержня l, можна визначити момент інерції фізичного маятника за формулою:
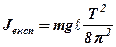(2. 2. 5)
Для підвищення точності розрахунків в роботі безпосередньо вимірюється час t, за який фізичний маятник здійснює N повних коливань.
Тоді період T буде дорівнювати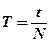 
і остаточно розрахункова формула експериментального визначення моменту інерції набуває вигляду
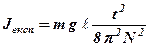(2. 2. 6)
З іншого боку, момент інерції довгого стержня відносно осі, яка проходить через його кінець, можна знайти за формулою (2. 2. 2).
Порядок вимірювання та розрахунків:
1. Підготувати таблицю для запису результатів вимірювань.
2. Визначити масу маятника m i також довжину стержня ℓ від його кінця до точки закріплення, внести до протоколу.
3. Виміряти час N повних коливань маятника i результати внести до таблиці. Вимірювання повторити 5 разів.
4. Обчислити середній час коливань i похибку вимірювань.
5. Розрахувати експериментальні значення моменту інерції маятника, середнє значення моменту інерції, його похибку.
6. Розрахувати теоретичне значення моменту інерції стержня, порівняти з середнім експериментальним значенням, зробити висновок.
|
|
|
