 |
3.2.1. Закони постійного струму.
|
|
|
|
1. Постійний струм може текти тільки в замкненому колі.
2. Сила струму через будь – який переріз провідника однакова (якщо не має розгалуження). В протилежному випадку відбувалось би накопичування зарядів.
3. Закон Ома для однорідної ділянки кола. Однорідною ділянкою кола будемо називати ділянку кола, в якій немає сторонніх сил. Сила струму на ділянці кола прямо пропорційна різниці потенціалів на кінцях ділянки:
(3. 34)
Величина R називається опором ділянки кола. Для однорідного провідника довжиною l та площею поперечного перерізу S справедлива формула для опору:
(3. 35)
Величина r має назву питомого опору. Величина, обернена питомому опору, називається питомою електропровідністю
(3. 36)
Для металевих провідників питомий опір збільшується лінійно з температурою t (в градусах Цельсія):
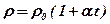(3. 37)
Величина a називається температурним коефіцієнтом опору, r0 – питомий опір при температурі 0 оС.
Для деяких провідників при низьких температурах відбувається явище надпровідності, коли опір стрибком зменшується до нуля. Це явище було відкрите для ртуті Камерлінгом – Оннесом в 1911 році. Температура переходу в надпровідний стан становила 4. 15 К. Для інших металів та сплавів температурі інші, але також низькі.
4. Закон Джоуля – Ленца. На ділянці кола безперервно відбувається виділення теплоти. Кількість теплоти, яка виділяється на ділянці кола, прямо пропорційна квадрату сили струму, опору провідника та часу протікання струму, тобто
|
|
|
(3. 38)
5. 
Закон Ома для неоднорідної ділянки кола. Якщо в колі існують сторонні сили, то таку ділянку будемо називати неоднорідною. Розглянемо таку ділянку, яка складається з опору R (зовнішнього опору) та джерела струму з ЕРС ε та внутрішнім опором r (рис. 3. 1).
Запишемо кількість теплоти, що виділяється на цій ділянці за час dt згідно з законом Джоуля – Ленца, а також врахуємо, що добуток сили струму на час протікання струму дає перенесений за цей час заряд:
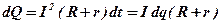(3. 39)
Згідно з законом збереження енергії ця теплота повинна дорівнювати роботі всіх сил по переміщенню заряду dq уздовж кола, тобто
(3. 40)
Прирівнюючи вирази (3. 39) і (3. 40), скорочуючи на заряд dq обидві частини рівності, для сили струму знайдемо:
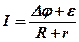(3. 40)
Це математичний вираз закону Ома для неоднорідної ділянки кола: сила струму на неоднорідній ділянці кола прямо пропорційна напрузі між кінцями кола (складається з різниці потенціалів та електрорушійної сили) та обернено пропорційна загальному опору ділянки кола (складається з зовнішніх та внутрішніх опорів).
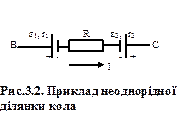Розглянемо частинні випадки. Якщо коло замкнене, тобто точки В та С збігаються, то Dj = 0 ( jВ = jС ) і тоді ми приходимо до закону Ома для замкненого кола у вигляді 
(3. 41)
Нехай тепер немає джерела струму, тобто ε = 0, r = 0. Тоді ми прийдемо до закону Ома для однорідної ділянки кола у вигляді (3. 34).
|
|
|
Для використання закону Ома для неоднорідної ділянки кола необхідно встановити правила знаків. По – перше, необхідно обрати один з двох напрямів уздовж ділянки кола за позитивний. Далі, електрорушійна сила буде мати позитивний знак, якщо напрям напруженості поля сторонніх сил (від негативного полюсу джерела струму до позитивного) збігається з позитивним напрямом. Якщо ж ці напрями протилежні, то ЕРС буде негативною. Сила струму буде мати позитивний знак, якщо позитивні носії струму рухаються уздовж позитивного напряму, і негативний у протилежному напрямку.
Розглянемо це на прикладі кола, зображеного на рис. 3. 2. Закон Ома в цьому випадку буде мати такий вигляд 
. Якщо при підстановці чисельних значень виходить, що сила струму буде негативною за знаком, то це означає, що струм насправді тече в протилежному напрямі, тобто від точки С до точки В.
6. Закон Ома в диференціальній формі.
Розглянемо провідник, уздовж якого протікає електричний струм. Виділимо всередині провідника малий прямий циліндр довжиною dl та площею основи dS. Якщо провідник однорідний, то закон Ома для цього малого циліндра буде мати вигляд:
,
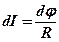де dj - різниця потенціалів між кінцями циліндра, R – його опір. Останній можна записати через питомий опір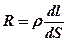 
. Крім того, силу струму можна виразити через густину струму 
. Тоді одержимо 
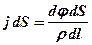. Скорочуючи обидві частини рівності на dS, а також враховуючи закон між напруженістю та потенціалом, одержимо
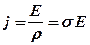(3. 42)
Останній вираз запишемо також у векторній формі
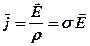(3. 43)
Нехай тепер в колі присутні сторонні сили. Тоді в правій частині рівності треба додати також напруженість поля сторонніх сил:
(3. 44)
7. Закон Джоуля – Ленца в диференціальній формі.
Розглянемо як і раніше частину провідника у вигляді малого прямого циліндра довжиною dl та площею основи dS. При протіканні електричного струму відбувається виділення теплоти, кількість якої згідно з законом Джоуля – Ленца пропорційна квадрату сили струму, опору циліндра та часу протікання струму, тобто
|
|
|
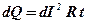(3. 45)
Врахуємо зв’язок між силою струму та густиною струму, а також перепишемо опір провідника через питомий опір та його розміри:
Введемо в розгляд величину – питому потужність, яка дорівнює відношенню кількості теплоти, що виділяється в деякому об’ємі за деякий час, до величини цього об’єму та часу:
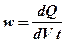(3. 46)
Тоді поділивши рівність (3. 45) на dV та t, одержимо, що питома потужність прямо пропорційна квадрату густини струму та питомому опору ділянки провідника. Використовуючи закон Ома в диференціальній формі, можна одержати також ще дві форми запису закону Джоуля – Ленца:
(3. 47)
8. Правила Кірхгофа для розгалужених кіл постійного струму.
Ми будемо розглядати сукупність нерозгалужених ділянок, кінці яких з’єднуються в вузлах. Вузол – це точка, в якій перетинаються три або більше провідника. В усіх перерізах однієї ділянки сила струму однакова. Але в різних ділянках сила струму різна. Зрозуміло, що сума сил струмів, які втікають у вузол, повинна дорівнювати сумі сил струмів, які витікають з вузла. Якщо б це було не так, то заряд накопичувався б у вузлі. Запишемо це так:
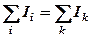
Тут в лівій частині рівності струми, які втікають у вузол, а в правій частині – які витікають. Домовимось вважати струми, що втікають у вузол, позитивними, а струми, які витікають з вузла, негативними. Тоді можна сформулювати перше правило Кірхгофа так: алгебраїчна сума сил струмів, які сходяться у вузлі, дорівнює нулю. Тобто
(3. 48)
Для формулювання другого правила Кірхгофа необхідно розглянути контур - сукупність замкнених ділянок. Для будь – якого контуру сума спадів напруги (добутків сили струму на опір) на усіх ділянках контуру дорівнює сумі електрорушійних сил, які діють в контурі. Математичний запис цього правила такий:
|
|
|
(3. 49)
Для використання правил Кірхгофа необхідно використовувати, як і раніше, правила знаків. Розглянемо застосування правил Кірхгофа на прикладі, зображеному на рис. 3. 3.
По – перше, знайдемо вузли в схемі: це точки F та С. Оберемо довільно напрями сил струмів І1, І2, І3, наприклад, так, як вказано на рисунку. Застосуємо перше правило Кірхгофа для одного з вузлів, наприклад, С:
І1 + І2 - І3 = 0 (3. 50)
Можна перевірити, що для другого вузла рівняння буде таким самим. Для застосування другого правила Кірхгофа треба взяти два контури з трьох – нехай це будуть FCBAF та FDECF. Будемо обходити ці контури проти руху годинникової стрілки. Дістанемо тоді відповідно:
І2 (R2 +r2) – І1 (R1 +r1) = -ε 2 – ε 1, (3. 51)
- І3 (R3 +r3) – І2 (R2 +r2) = ε 3 + ε 2 (3. 52)
Сила струму вважається позитивною, якщо напрям обходу контуру збігається з напрямом струму, і негативною, якщо ці напрями протилежні. Знак ЕРС обирається позитивним, якщо при обході контуру спочатку зустрічається негативний полюс джерела струму, а далі позитивний, у випадку, коли спочатку зустрічається позитивний полюс джерела струму, а потім негативний, ЕРС вважається негативною. Далі розв’язується система рівнянь (3. 50) – (3. 52) для знаходження сил струмів при умові, що задаються значення ЕРС і усіх опорів. Якщо значення сили струму виявиться негативним, то це означає, що струм насправді тече в протилежному до обраного напрямку.
|
|
|
