 |
Методы решения ЗВМ, основанные на свертывании
|
|
|
|
(скаляризации) критериев
Данный метод заключается в формировании на основе дополнительной информации, полученной от лица, принимающего решения, функциональной зависимости между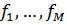 
и построение на ее основе скалярной функции для задачи оптимизации, которая бы сыграла роль нового принципа и которую будем называть обобщенной функцией критериев. Процедуру построения такой функции будем называть скаляризацией критериев ЗВМ. Идея скаляризации критериев впервые, по-видимому, введена Карлиным [1]. Им же доказаны теоремы, обосновывающие справедливость подхода.
Рассмотрим достижимое множество ЗВМ:
При этом будем полагать, что частные критерии ЗВМ являются дважды непрерывно дифференцируемыми функциями.
Определение 1. Под обобщенной функцией критериев в задаче векторной максимизации будем понимать дважды непрерывно дифференцируемую функцию 
такую, что если точка 
доминирует по Парето точку 
достижимого множества, то 
Свойства обобщенной функции критериев:
1) Обобщенная функция критериев является дважды непрерывно дифференцируемой (данное свойство непосредственно следует из определения);
2) Суперпозиция обобщенной функции и монотонно возрастающей функции является обобщенной функцией критериев;
3) Обобщенная функция является покоординатно возрастающей.
Доказательства свойств обобщенной функции критериев рассмотрены в следующих теоремах.
Теорема 1. Пусть 
- дважды непрерывно дифференцируемая, монотонно возрастающая функция, а 
- обобщенная функция. Тогда 
являются обобщенной функцией в задаче векторной максимизации.
Доказательство. Пусть доминирует по Парето точку достижимого множества. Тогда по определению 
что в силу монотонного возрастания функции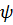 
означает: 
а следовательно, функция является обобщенной функцией. Теорема доказана.
|
|
|
Замечание 1. Обобщенные функции 
упомянутые в теореме 1, называются эквивалентными.
Теорема 2. Обобщенная функция 
является покоординатно возрастающей.
Доказательство. Покоординатное возрастание означает, что для любого i скалярная функция: 
является возрастающей.
Здесь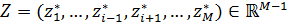 
- произвольный фиксированный вектор.
Рассмотрим векторы достижимого множества:
где 
а остальные координаты фиксированы. Тогда вектор 
доминирует вектор 
, а следовательно 
Теорема доказана.
В соответствии с введенным выше определением может быть сформирован принцип оптимальности, заключающийся в необходимости выявления альтернативы, максимизирующей функцию 
на допустимом множестве:
Пусть 
- решение задачи (6):
Тогда справедливы следующие теоремы.
Теорема 3. Пусть 
– обобщенная функция ЗВМ, - решение задачи (6). Тогда – эффективная точка задачи векторной максимизации.
Доказательство
Предположим противное. Пусть - решение задачи (6), не является Парето – оптимальной точкой. Тогда существует точка 
такая, что 
и существует такой индекс j, что 
В силу покоординатного возрастания функции имеем: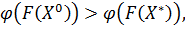 
что противоречит условию оптимальности точки 
Что и требовалось доказать.
Теорема 4. Если в выпуклой задаче векторной максимизации точка оптимальна по Парето, то существует такая обобщенная функция критериев 
что 
– решение задачи (6).
Доказательство теоремы 4 построено на предположении искать обобщенную функцию в виде:
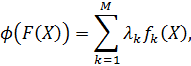
где
Для доказательства требуется ряд дополнительных фактов, после приведения которых теорема 6, из которой следует обсуждаемый нами факт, будет доказана.
В качестве обобщенной функции критериев ЗВМ может быть выбрана из приведенных ниже функций.
1. Функция полезности лица, принимающего решения.
|
|
|
2. Аддитивная свертка критериев:
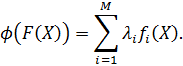
3. Мультипликативная свертка критериев:
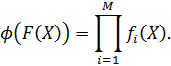
4. 
5. 
При этом 
- весовые коэффициенты, характеризующие важность (приоритетность) критериев,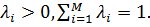 
Функция полезности лица, принимающего решения (ЛПР)
Предположим, что ЛПР обладает системой предпочтений на допустимом множестве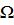 
задачи векторной максимизации или, что равносильно, на достижимом множестве
Тогда в качестве обобщенной функции критериев возможно использовать функцию полезности ЛПР, позволяющую на множестве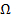 
выделить лучшую в смысле предпочтений ЛПР точку, которая и будет являться решением ЗВО.
Таким образом, будем предполагать, что на множестве 
задано бинарное отношение нестрогого предпочтения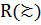 
такое, что
1) если 
2) если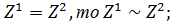 
3) если 
не связаны отношениями 1) и 2), то ЛПР может сравнить 
по предпочтению и сказать, что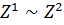 
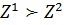, или 
, или 
.
Введенное бинарное отношение обладает следующими свойствами:
1) полнота (связность);
2) рефлексивность;
3) транзитивность;
4) если 
если 
, то .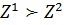
Определение 2. Функцию 
такую, что для любых векторов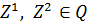 
справедливо:
;
,
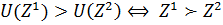называют порядковой функцией полезности критериальных векторов.
В силу определения и свойств отношения предпочтения, порядковая функция полезности является обобщенной функцией критериев.
В работах [5], [8] списка дополнительной литературы доказаны теоремы, касающиеся условий существования функций полезности, заданных на произвольном множестве Конструктивное же построение такой функции опирается, как правило, на следующую информацию от ЛПР:
1) информация количественного типа, основанная на замещениях: для фиксированного значения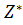 
вектора 
указывается равноценное ему значение 
;
2) Информация, основанная на интерпретации значений лингвистической переменной. Здесь ЛПР для несравнимой по Парето пары значений 
указывает соответствующее их сравнению значение лингвистической переменной – приблизительно равноценны, чуть лучше, значительно лучше и т.д.;
3) Информация в порядковой шкале. ЛПР сравнивает пару векторов в форме лучше, хуже, безразличны.
Однако, если для решения реальной задачи не предоставлена возможность получения непротиворечивой информации, достаточной для построения функции полезности ЛПР, в качестве обобщенной функции могут быть использованы функции 2-5. Наиболее распространенной на практике обобщенной функцией критериев является аддитивная свертка критериев:
|
|
|
Метод решения ЗВО, базирующийся на построении аддитивной свертки, получил название «Метод взвешенных сумм».
Метод взвешенных сумм
Согласно данному методу, задаче векторной максимизации (2) ставится в соответствие задача скалярной максимизации вида:
(8)
где 
Рассмотрим множество 
.
Рассмотрим теоремы, касающиеся свойств полученного решения, доказанные Карлиным в работе [1].
Частным случаем теоремы 3 является:
Теорема 5. Пусть 
. Тогда решение задачи:
есть эффективный (Парето–оптимальный) вектор.
Замечание 1. Обратное утверждение без дополнительных предположений неверно. Существуют эффективные векторы, не являющиеся решением задачи (8). Однако для выпуклых задач векторной максимизации справедливость обратного утверждения докажем в теореме 6, предварительно рассмотрев ряд вспомогательных понятий и лемм.
Пусть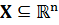 
– произвольное множество. Наименьшее выпуклое множество 
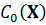, содержащее данное множество X, называется выпуклой оболочкой множества X, т.е.:
,
где r – произвольное натуральное число.
Рассмотрим выпуклое множество .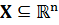
Множество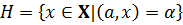 
,
где 
(
) – вектор пространства 
, 
- число, 
, называется гиперплоскостью.
Гиперплоскость 
определяет два замкнутых полупространства 
, 
, которые являются замкнутыми выпуклыми множествами.
Гиперплоскость называется опорной к выпуклому множеству 
, если содержится в одном из полупространств, определяемых , и граница имеет с хотя бы одну общую точку. Таким образом, гиперплоскость является опорной для множества , если:
.
В работе [1] списка дополнительной литературы доказаны следующие леммы.
Лемма 1. Пусть X – выпуклое множество, а y - точка, внешняя относительно замыкания X. Тогда существует такой вектор a, что
Лемма 2. Пусть X – выпуклое множество, а y лежит на границе X. Тогда существует опорная плоскость, проходящая через y, т.е. существует такой ненулевой вектор а, что
|
|
|
.
Лемма 3. Если X, Y – выпуклые множества, не имеющие общих внутренних точек, то существует гиперплоскость H, которая разделяет 
и 
, т.е. существуют такие ненулевой вектор 
и число α, что 
для всех 
и 
для всех 
На основании представленных лемм докажем следующую лемму.
Лемма 4. Пусть - выпуклое множество, не имеющее общих точек с неотрицательным ортантом пространства . Тогда существует такой вектор 
Доказательство. Пусть Y – неотрицательный ортант пространства . Согласно леммы 3, в силу выпуклости X и Y существует ненулевой вектор a и число такое, что:
для всех 
для всех
В качестве такой плоскости H можно выбрать опорную гиперплоскость к Y, проходящую через граничную точку 0 неотрицательного ортанта. Тогда, согласно лемме 2:
Таким образом,
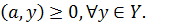(9)
Докажем, что все компоненты ненулевого вектора a неотрицательны.
Рассмотрим неравенство (9), положив 
где 1 стоит на i- м месте. Тогда 
откуда следует, что 
для любого 
. Лемма доказана.
Теорема 6. Если в выпуклой задаче векторной максимизации 92) точка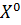 
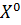оптимальна по Парето, то существует вектор весовых коэффициентов , для которого точка является решением задачи скалярной максимизации (8), т.е.
Доказательство. Рассмотрим множество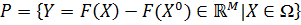 
, а через K означим выпуклую оболочку множества . Так как 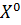- эффективная точка, то 
не может содержать векторы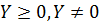 
и, следовательно, не может совпадать с внутренностью неотрицательного ортанта пространства 
. Из вогнутости целевых функций задачи и эффективности точки 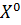следует, что множество K не содержит внутренних точек неотрицательного ортанта. Тогда в силу леммы 4 существует гиперплоскость 
, которая отделяет K от неотрицательного ортанта, где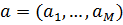 
, 
и существует индекс j: 
.
Положим
Тогда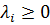 
, 
, 
.
Докажем, что 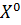является решением задачи (8) с построенными весовыми коэффициентами. Согласно леммы 4, выполнены неравенства 
, тогда 
, что в силу свойства скалярного произведения равносильно неравенству 
, а следовательно, в силу неотрицательности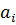 
выполнено неравенство:
что означает, что
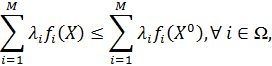
т.е. 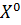- решение задачи (8). Теорема доказана.
Таким образом, согласно теореме 5, все точки, максимизирующие аддитивную свертку критериев ЗВМ, являются эффективными, если вектор весов строго положителен. По теореме 6, каждой эффективной точке выпуклой ЗВМ можно поставить в соответствие весовой вектор 
, для которого задача максимизации взвешенных сумм имеет эту эффективную точку своим решением.
Рассмотрим несколько примеров.
Пример 1. Рассмотрим ЗВМ:
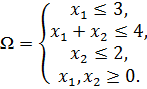
Для каждого значения параметра 
найти решение задачи методом взвешенных сумм.
|
|
|
Решение. Допустимое множество задачи изображено на рисунке 5.
Графическое решение задачи показывает, что множеством Парето-оптимальных точек является отрезок [B,C].
Рассмотрим задачу максимизации аддитивной свертки критериев:
(10)
Покажем, что при 
и 
решением взвешенной задачи могут являться точки, которые не эффективны в исходной ЗВМ, и найдем, при каких 
решением скалярной задачи является каждая эффективная точка.
1. Если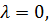 
то 
, градиент функции направлен перпендикулярно отрезку [A,B], все точки которого, за исключением B, не являются эффективными.
2. Если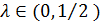 
, то решением задачи (10) является Парето–оптимальная точка B.
3. При 
градиент функции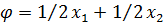 
направлен перпендикулярно отрезку [B,C], и решением задачи (10) является этот отрезок.
4. При 
решением является эффективная точка C.
5. Если 
то 
, градиент функции направлен перпендикулярно отрезку [C,D], все точки которого, за исключением C, являются неэффективными.
Пример 2. Рассмотрим задачу векторной максимизации с областью, представленной на рисунке 6, и функциями цели:
Допустимая область задачи не является выпуклой и не удовлетворяет условиям теоремы 6. Точки дуги (a,b) являются оптимальными по Парето, но ни одна из них (кроме самих точек a и b) не может являться точкой максимума функции 
ни прикаких .
Пример 3. Для задачи векторной максимизации:
известно, что функция полезности лица, принимающего решения, имеет вид: 
.
Найти эффективную точку допустимого множества, в которой функция полезности принимает наибольшее значение.
Решение. Рассмотрим 2 способа решения поставленной задачи: в пространстве решений и в критериальном пространстве.
1. Для решения задачи в пространстве решений перепишем функция полезности в терминах переменной 
. Допустимая область и линии уравнения 
функции изображены на рисунке 7.
Графически решая задачу, найдем оптимальную точку 
2. Для решения задачи в критериальном пространстве рассмотрим достижимое множество, изображенное на рисунке 8.
Графически изображая в критериальном пространстве линии уровня функции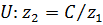 
, находим решение задачи – точку 
, которая является образом точки
Упражнения к § 4
№ 1. Для задач векторной максимизации с заданной функцией полезности ЛПР найти решение в пространстве решений и критериальном пространстве:
1) 
.
2)
.
3)
.
№ 2. Решить методом взвешенных сумм
1) 
, 
, 
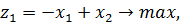
2)
, 
, 
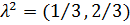№ 3. Для задачи векторной максимизации определить, при каких значениях оптимальным решением задачи с взвешенными суммами будут перечисленные точки.
1)
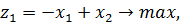
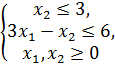
а) отрезок [A,B]; b) точка B; c) точка C; d) отрезок [B,C], где A=(0,0), В=(0,3), С=(3,3).
2) 
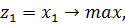
а) отрезок [A,B]; b) точка B; c) точка C; d) отрезок [B,C], где A=(3,0), В=(
), С=(
).
№ 4. Определить графически все подмножества 
, соответствующие каждой эффективной грани в следующих задачах:
1) 
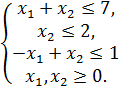
2) 
№ 5. Пусть модель автомобиля оценивается по 2 характеристикам: надежность (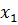
), максимальная скорость передвижения (
). Причем автомобиль может быть сконструирован с любой комбинацией данных характеристик, удовлетворяющих системе ограничений:
Критерии выбора 
, 
.
При условии, что функция полезности лица, принимающего решение, неизвестна, проанализировать, какой тип сверки возможно использовать при решении задачи. Решить задачу с аддитивной и мультипликативной свертками, полагая, что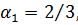 
№ 6. В рамках эксперимента введены единые государственные экзамены по математике и английскому языку. Школьник имеет 100 дней для подготовки к тестам. Оценка, полученная на экзамене, измеряется в 100-балльной шкале и, по прогнозам, пропорциональна количеству дней, затраченных на подготовку к экзамену по данному предмету. Школьник желает получить максимальный балл по каждому предмету. Требуется распределить количество дней на подготовку к каждому экзамену.
Составить модель задачи. Какой тип обобщенной функции может использовать школьник, если по результатам тестов он поступает на факультет, на котором принимаются результаты по:
a) математике; b) английскому; c) ни по математике, ни по английскому; d) по обоим предметам.
|
|
|
