 |
Методы решения ЗВМ, основанные на лексикографическом принципе оптимальности
|
|
|
|
Рассмотрим ЗВМ (2):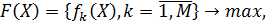 
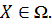
В основе лексикографического принципа оптимальности, позволяющего сократить множество Парето-оптимальных точек, лежит предположение о строгой упорядоченности по важности частных критериев 
. Введем в рассмотрение следующие определения.
Определение 1. Нормированный критерий 
более важен, чем критерий 
, если векторная оценка
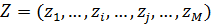, менее предпочтительна, чем оценка
, где 
.
Таким образом, перенос 
единиц с частной оценки 
на частную оценку 
приводит к улучшению ситуации.
Определение 2. Нормированные критерий и 
называются равноценными (
), если любые две векторные оценки 
:
,
)
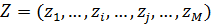одинаковы по предпочтительности для любого .
Таким образом, будем считать, что частные критерии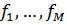 
упорядочены по важности так, что при сравнении пары альтернатив в первую очередь используется первый критерий 
, и лучшей считается та точка допустимого множества, для которой значение этого критерия больше; если значения первого критерия для обоих векторов оказываются равными, то применяется второй критерий, и предпочтение отдается той точке, для которой его значение больше; если и второй критерий не позволяет выделить лучшую альтернативу, привлекается третий частный критерий и т.д. до 
. Если же значения каждого частного критерия для рассматриваемых альтернатив оказываются равными, то эти альтернативы считаются эквивалентными, т.е. равноценными в смысле векторного критерия 
.
Указанное лексикографическое отношение предпочтения формально задается следующим образом.
Определение 3. Вектор 
предпочтительнее вектора 
(
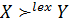), если выполнено одно из 
условий (17):
1) 
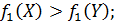
2) 
…
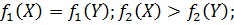
r)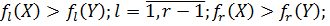 
…
M)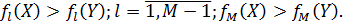 
Определение 4. Векторы и называются эквивалентными (
), если выполнено условие:
|
|
|
(18)
Определение 5. Вектор 
лексикографически не хуже (не менее предпочтителен), чем вектор 
(
), если выполнено одно из условий (17) или же (18).
Важно подчеркнуть, что любые две альтернативы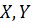 
сравнимы по введенному выше отношению предпочтения, т.е. всегда выполняется одно из трех условий:
1) 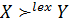; 2) ; 3) 
.
Определение 6. Лексикографически оптимальной называется точка 
, которая не хуже любой другой альтернативы 
в смысле отношения 
, т.е. если 
.
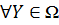Пусть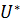 
- множество всех лексикографически оптимальных стратегий.
Множество 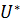можно задать с помощью рекуррентных соотношений:
(19)
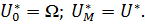
Из этих соотношений вытекает, что
,
т.е. каждый последующий частный критерий сужает множество стратегий, получаемых с помощью всех предыдущих частных критериев.
Замечание 1. В общем случае 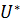может оказаться пустым. Однако лексикографическая задача будет иметь решение и притом единственное, если какой-либо критерий 
обращается в максимум на 
в единственной точке.
Итак, лексикографическая задача оптимизации заключается в отыскании лексикографически оптимальных стратегий и в случае их существования записывается в следующем виде.
Найти
(20)
Рассмотрим вопрос отыскания лексикографически оптимальных стратегий. При этом следует отметить, что решать лексикографическую задачу (20) с помощью рекуррентных соотношений (19) с вычислительной точки зрения сложно, поскольку на каждом этапе (кроме, быть может, последнего) необходимо строить множества 
. В силу этого удобнее решать последовательность задач, изложенных в алгоритме 1.
Алгоритм 1. Алгоритм решения ЗВМ с лексикографическим принципом оптимальности
Шаг 0. Рассматривается задача векторной максимизации (2); - частные критерии задачи 
, которые строго упорядочены по важности: 
; 
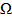– допустимое множество.
Шаг 1. Решение частной задачи вида:
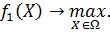
Пусть 
- множество решений задачи,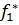 
- оптимальное значение функции цели.
|
|
|
Если состоит из одной точки, переход к Шагу 4, иначе –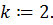 
Шаг 2. Решение задачи вида:
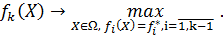
Пусть - множество решений задачи, 
- оптимальное значение функции цели.
Шаг 3. Если состоит из одной точки или 
, то переход к шагу 4. Иначе 
, переход к шагу 2.
Шаг 4. Останов. - множество лексикографически оптимальных решений задачи (2).
Следующая теорема позволяет установить связь между лексикографически оптимальными и эффективными векторами ЗВМ.
Теорема 1. Всякая лексикографически оптимальная стратегия является эффективной.
Доказательство. Пусть 
- лексикографически оптимальная стратегия ЗВМ, т.е. 
является решением задачи (20).
Предположим противное: пусть не является эффективной. Тогда существует вектор такой, что:
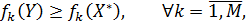
и существует 
.
Рассмотрим индекс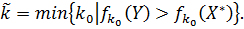 
Тогда 
и 
, откуда следует, что 
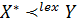, что противоречит лексикографически оптимальной точке. Получили противоречие с определением 6, и, следовательно, является Парето–оптимальной точкой.
|
|
|
