 |
Методы решения ЗВМ произвольной структуры
|
|
|
|
Рассмотрим задачу векторной максимизации
,
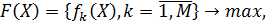
где Ω – ограниченное множество, а на функции 
ограничения не накладываются.
Для решения ЗВМ произвольной структуры предлагается использовать алгоритм, включающий процедуры дискретизации и фильтрации множеств. Под дискретизацией бесконечного множества понимается его репрезентативное представление конечным числом точек. Фильтрация означает замену конечного множества его «разреженным» подмножеством посредством исключения некоторых из «близких» в определенном смысле точек.
Алгоритм 1. Алгоритм решения ЗВМ произвольной структуры
Шаг 1. Дискретизация допустимого множества Ω, т. е. замена его множеством 
, состоящим из конечного числа точек множества Ω.
Шаг 2. Фильтрация множества , т. е. построение разреженного множества 
.
Шаг 3. Построение множества эффективных точек 
задачи:
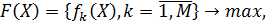
Шаг 4. Выбор наилучших с точки зрения ЛПР точек множества . Останов.
Остановимся более подробно на описании процедур дискретизации и фильтрации множеств.
Дискретизация множеств
Рассмотрим многогранник Ω, число вершин которого равно K. Требуется построить конечное подмножество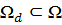 
мощностью L, представляющее множество Ω.
Если 
то множество 
включает вершины многогранника, и поэтому будем рассматривать случай 
.
Пусть 
– вершины многогранника Ω. Тогда для любой точки
существуют такие числа 
(
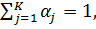
), что справедливо следующее представление:
(30)
Тогда исходная задача сводится к задаче формирования 
наборов весовых коэффициентов 
. Для этого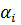 
генерировать с помощью датчика случайных чисел, применяя следующую формулу:
Если числа 
получаются как результат генерирования случайных чисел, равномерно распределенных на отрезке [0,1], то точки X, получаемые в соответствии с (30), образуют сгущения вокруг центра многогранника.
|
|
|
Для получения точек Х, расположенных в близости к границам многогранника, необходимо 
генерировать с помощью распределения Вейбулла:
где 
- случайные числа, равномерно распределенные на (0,1); b, c – параметры распределения (например, b =0,1, c =0,3).
Для адекватного представления многогранника Ω конечным числом точек при выборе весовых коэффициентов в (30) предлагается использовать стратегию «50-50» - генерировать 50 процентов весовых векторов выпуклых комбинаций с помощью равномерного распределения и 50 процентов – с помощью распределения Вейбулла. В этом случае генерируемые точки Х располагаются не только в центре многогранника, но и в его углах.
Фильтрация множеств
Естественным способом разрежения набора точек, которые получены в результате процесса дискретизации, для более полного и равномерного представления допустимого множества используются процедуры, названные фильтрацией. Различают прямую и обратную фильтрацию.
Прямая фильтрация заключается в выделении P точек, отстоящих друг от друга на расстоянии, не меньше наперед заданного.
Обратная фильтрация заключается в формировании P точек, лежащих в окрестности наперед заданной точки.
Таким образом, прямая фильтрация применяется для «прореживания» множества точек, а обратная – для выделения точек в заданной области.
Пусть 
– конечное множество векторов. Процессы прямой и обратной фильтрации основаны на сравнении расстояния между парами векторов 
вычисляемого по формуле:
где 
– вес для выравнивания диапазона, соответствующий i -й координате выравниваемых векторов; p – параметр метрики,.
Веса для выравнивания диапазона предназначены для выравнивания разбросов векторов из V:
,
где
|
|
|
Рассмотрим алгоритмы прямой фильтрации множеств, среди которых выделяют следующие:
1) метод первой точки вне окрестности;
2) метод ближайшей точки вне окрестности;
3) метод наиболее удаленной точки вне окрестности.
Во всех перечисленных методах применятся отношение фильтрации, предназначенное для сравнения взвешенных расстояний между точками, которые еще не «задержаны» фильтром, и точками, уже «задержанными». Отношение фильтрации задается в виде:
где 
– вектор, который еще не задержан фильтром; 
– задержанный фильтром вектор. Параметр прямой фильтрации регулирует отношение фильтрации следующим образом: если расстояние между точками и больше или равно d, то эти точки считаются существенно отличающимися. В противном случае точки считаются несущественно отличающимися.
Метод первой точки вне окрестности
Метод первой точки вне окружности запишем в виде последовательностей шагов алгоритма 2.
Алгоритм 2. Алгоритм фильтрации множества методом первой точки вне окрестности
Шаг 0. Начальные данные: 
– исходное множество векторов с заданной последовательностью точек; d – радиус окрестности; 
– множество векторов, задержанных фильтром.
Шаг 1. 
– первая точка, задержанная фильтром; 
Шаг 2. Если 
, то перебирая последовательно точки множества 
, находим первую такую точку 
что 
(т.е. 
существенно отличается от отфильтрованных векторов).
Если такой точки в множестве нет, то переход к шагу 3, иначе –; 
.
Шаг 3. Останов,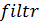 
– искомое множество отфильтрованных точек.
Замечание 1. Иногда требуется получить отфильтрованное множество векторов, содержащее P точек. В этом случае задают начальное d и реализуют шаги алгоритма 2.
Если 
, то начальное d увеличивают и снова осуществляют шаги алгоритма 2.
Если 
, то начальное d уменьшают и осуществляют алгоритм 2.
Процесс продолжают до тех пор, пока не будет найдено такое d, что 
. При этом может применяться стратегия удвоения и деления d пополам. В этом случае процесс многократных запусков алгоритма 2 сходится к множеству желаемого числа точек.
Замечание 2. Множество точек, задержанных фильтром методом первой точки вне окрестности, зависит как от начальной точки, так и от порядка обработки точек.
|
|
|
Замечание 3. Можно рассмотреть и вариант процесса прямой фильтрации с несколькими начальными точками. Эти точки помещаются в верхней части списка и обязательно задерживаются фильтром. Все остальные точки фильтруются обычным способом.
Метод ближайшей точки вне окрестности
В отличие от метода первой точки вне окрестности, когда фильтром задерживается первая по порядку в списке точка, существенно отличающаяся от уже задержанных фильтром, в предлагаемом методе среди всех точек, существенно отличающихся от задержанных фильтром, задерживается та, сумма расстояний от которой до элементов множества 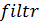минимальна. Приведем шаги алгоритма.
Алгоритм 3. Алгоритм фильтрации множества методом ближайшей точки вне окрестности
Шаг 0. Начальные данные: – исходное множество точек; d – радиус окрестности; – множество векторов, задержанных фильтром; 
– множество векторов, существенно отличающихся от задержанных фильтром.
Шаг 1. 
– первая точка, задержанная фильтром;
Шаг 2. Если , то переход к шагу 4, иначе заполняем множество S такими точками из 
, которые существенно отличаются от точек множества 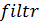, перебирая
Если множество 
, то переход к шагу 4.
Шаг 3. Выбор ближайшей точки вне окрестности, т.е. находим точку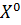 
:
, 
переход к Шагу 2.
Шаг 4. Останов, 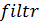– искомое множество отфильтрованных точек.
Замечание 4. Метод ближайшей точки вне окрестности не зависит от порядка обработки векторов, хотя зависимость от начальной точки остается.
Метод наиболее удаленной точки вне окрестности
Этот метод идентичен методу ближайшей точки вне окрестности, за исключением способа выбора каждой следующей точки, задерживаемой фильтром. Вместо того, чтобы выбирать существенно отличающуюся точку, имеющую наименьшую сумму расстояний от всех точек, уже задержанных фильтром, выбирается существенно отличающаяся точка наибольшей суммой расстояний.
Алгоритм метода наиболее удаленной точки вне окрестности аналогичен алгоритму 3 за исключением шага 3:
Шаг 3*. Выбор наиболее удаленной точки вне окрестности, т. е. находим точку :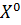
|
|
|
, переход к Шагу 2.
Обратная фильтрация
Под обратной фильтрацией понимают процедуру выбора заданного числа точек из списка, ближайших к наперед заданной.
Пусть – множество векторов, которое нужно обработать с помощью процедуры обратной фильтрации. Пусть – обратная начальная точка (расположенная в начале списка из точек перед «подачей» в фильтр). При обратной фильтрации устанавливается порядок точек (от ближайшей до самой удаленной) в соответствии с их расположением от обратной начальной точки . Если 
– объем обратного множества, то в процессе обратной фильтрации получаем точку и 
ее ближайших соседей, которые образуют обратный список. Приведем шаги алгоритмов реализации процедуры обратной фильтрации для случаев, когда: 1) задан радиус окрестности точки; 2) задано число точек конечного списка.
Алгоритм 4. Алгоритм метода обратной фильтрации с заданным радиусом окрестности
Шаг 0. Начальные данные: – исходное множество точек; d – радиус окрестности; – обратная начальная точка;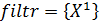 
– множество векторов, задержанных фильтром.
Шаг 1. Множество 
– искомое множество точек. Останов
Алгоритм 5. Алгоритм метода обратной фильтрации с заданным числом точек
Шаг 0. Начальные данные: 
– исходное множество точек; d – радиус окрестности; – обратная начальная точка; 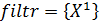–множество векторов, задержанных фильтром; – заданное число точек, задержанных фильтром.
Шаг 1. Для всех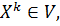 
вычисление расстояний 
Шаг 2. Упорядочение точек 
по возрастанию расстояний 
, т.е. формирование списка 
, где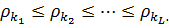 
Шаг 3. Множество задержанных фильтром векторов:
Останов.
Рассмотрим примеры, демонстрирующие работу алгоритмов.
Пример 1. Предположим, что семь точек, изображенных на рисунке 20, образуют список в порядке возрастания их номеров.
После прямой фильтрации списка с использованием первой точки вне окрестности, параметра метрики 
и радиуса окрестности 
фильтром задерживаются 4 точки: 
и 
. Точка задерживается как начальная, а точка 
– это первая точка вне - окрестности точек и 
. Точка задерживается как первая из точек, встреченных вне - окрестности точек .
Пример 2. Предположим, что семь точек, изображенных на рисунке 21, образуют список в порядке возрастания их номеров.
После прямой фильтрации списка с использованием ближайшей точки вне окрестности, параметра метрики и радиуса окрестности фильтром задерживаются 3 точки: 
и 
. Точка задерживается как начальная, а точка 
– это ближайшая точка вне - окрестности точки . Точка задерживается как ближайшая точка вне - окрестности точек и . Так как вне трех 
- окрестностей больше нет точек, то процесс закончен. Заметим, что если бы мы использовали метод первой точки вне окрестности, то задержались бы точк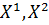и 
и .
|
|
|
Упражнения к § 9
№ 1. Вычислить расстояние от точки до 
, от до при 
.
№ 2. Вычислите веса для выравнивания диапазона для следующего множества векторов: 
; 
; 
; 
; 
; 
.
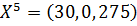№ 3. Использовав метод первой точки вне окрестностей и следующее множество точек: 
1) получите с помощью прямой фильтрации отфильтрованное множество мощности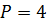 
, если параметр метрики и процедура фильтрации читает точки в порядке возрастания их индексов;
2) определите максимальное значение , при котором отфильтрованное множество имеет мощность .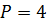
№ 4. То же самое, что и в задаче № 3, но с использованием ближайшей точки вне окрестности.
№ 5. То же самое, что и в задаче № 3, но с использованием наиболее удаленной точки вне окрестности.
№ 6. Использовав метод ближайшей точки вне окрестности и следующее множество точек:
1) получите с помощью прямой фильтрации отфильтрованное множество мощности 
, если параметр метрики и процедура фильтрации читает точки в порядке возрастания их индексов.
2) определите максимальное значение , при котором отфильтрованное множество имеет мощность .
№ 7. То же самое, что и в задаче № 6, но с использованием наиболее удаленной точки вне окрестности.
СПИСОК ЛИТЕРАТУРЫ
Основная литература
1. Машунин Ю.К. Теория управления. Математический аппарат управления в экономике / Ю.К. Машунин. – М.: Логос, 2013. – 448 с.
2. Моделирование систем и процессов / В.Н. Волкова, Г.В. Горелова, В.Н. Козлов [и др.]; под ред. В.Н. Волковой, В.Н. Козлова. – М.: Издательство Юрайт, 2014. – 592 с.
3. Постников В.М. Методы принятия решений в системах организационного управления: учеб. пособие / В.М. Постников, В.М. Черненький. – М.: Изд-во МГУ им. Н.Э. Баумана, 2014. – 205 с.
Дополнительная литература
1. Карлин С. Математические методы в теории игр, программировании, экономике / С. Карлин. – М.: Мир, 1964. – 838 с.
2. Машунин Ю.К. Методы и модели векторной оптимизации / Ю.К. Машунин. – М.: Наука, 1986. – 140 с.
3. Подиновский В.В. Парето-оптимальные решения многокритериальных задач / В.В. Подиновский, В.Д. Ногин. – М.: Наука, 1982. – 250 с.
4. Современный синтез критериев в задачах принятия решений / А.Н. Катулев, В.Н. Михно, Л.С. Виленчик и др. – М.: Радио и связь, 1992. – 120с.
5. Фишберн П. Теория полезности для принятия решений / П. Фишберн. – М. Наука, 1978. – 352 с.
6. Хоменюк В.В. Элементы теории многоцелевой оптимизации / В.В. Хоменюк. – М.: Наука, 1983. – 124 с.
7. Штойер Р. Многокритериальная оптимизация: теория, вычисления и приложения / Р. Штойер. – М.: Радио и связь, 1992. – 504 с.
|
|
|
