 |
Методы, использующие ограничения на критерии
|
|
|
|
Это направление включает два типа методов: метод ограничений и метод последовательных уступок.
Метод ограничений
Метод ограничений основан на введении лицом, принимающим решения, определенных ограничений на область изменения критериев.
На первом этапе одним из известных методов строится множество Парето  . Далее метод ограничений реализуется в соответствии со следующей последовательностью шагов.
. Далее метод ограничений реализуется в соответствии со следующей последовательностью шагов.
Алгоритм 1. Алгоритм решения ЗВМ методом ограничений:
Шаг 0. Рассматривается задача векторной максимизации (2);  частные критерии задачи
частные критерии задачи  .
.
Шаг 1. ЛПР предлагается назначить нижние допустимые границы  для всех
для всех  критериальных функций:
критериальных функций:
 . (21)
. (21)
Предполагается, что указанные значения функций дают удовлетворяющие пользователя варианты.
Шаг 2. Строится подмножество множества Парето, состоящее из точек, удовлетворяющих неравенствам (21):


Шаг 3. Если  - пустое множество, то ЛПР предлагается ослабить требование с помощью уменьшения какого-то из чисел
- пустое множество, то ЛПР предлагается ослабить требование с помощью уменьшения какого-то из чисел  , переход к шагу 2. Иначе – останов,
, переход к шагу 2. Иначе – останов,  - множество решений ЗВМ.
- множество решений ЗВМ.
Отметим, что на шаге 2 алгоритма множество  может быть сформировано, например, как решение одной из следующих задач:
может быть сформировано, например, как решение одной из следующих задач:
1) 


где  – обобщенный критерий;
– обобщенный критерий;
2) 


где  – наиболее важный критерий для ЛПР. В этом случае метод носит название метода главного критерия.
– наиболее важный критерий для ЛПР. В этом случае метод носит название метода главного критерия.
Метод последовательных уступок
При решении многокритериальной задачи методом последовательных уступок вначале производится качественный анализ относительной важности частных критериев, на основании которого критерии нумеруются в порядке убывания важности:  Максимизируется первый по важности критерий
Максимизируется первый по важности критерий  и определяется его наибольшее значение
и определяется его наибольшее значение 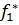 . Затем назначается величина “допустимого” снижения (уступки)
. Затем назначается величина “допустимого” снижения (уступки)  критерия
критерия  и ищется наибольшее значение
и ищется наибольшее значение  второго критерия
второго критерия  при условии, что значение первого критерия должно быть не меньше, чем
при условии, что значение первого критерия должно быть не меньше, чем  Снова назначается величина уступки Δ2 ≥ 0, но уже по второму критерию, которая вместе с первой используется для нахождения условного максимума третьего критерия и т.д. На последнем шаге максимизируется последний по важности критерий
Снова назначается величина уступки Δ2 ≥ 0, но уже по второму критерию, которая вместе с первой используется для нахождения условного максимума третьего критерия и т.д. На последнем шаге максимизируется последний по важности критерий  при условии, что значение каждого частного критерия
при условии, что значение каждого частного критерия 
 не меньше соответствующей величины
не меньше соответствующей величины  получаемые в итоге стратегии считаются оптимальными.
получаемые в итоге стратегии считаются оптимальными.
|
|
|
Таким образом, запишем метод последовательных уступок решения ЗВМ в виде шагов алгоритма 2.
Алгоритм 2. Алгоритм решения ЗВМ методом последовательных уступок
Шаг 0. Рассматривается задача векторной максимизации (2);  – частные критерии задачи (
– частные критерии задачи ( которые строго упорядочены по важности:
которые строго упорядочены по важности:  ;
; 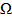 – допустимое множество.
– допустимое множество.
Шаг 1. Решение задачи:

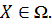
Пусть 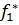 – оптимальное значение функции цели. Назначается величина “допустимого” снижения первого критерия
– оптимальное значение функции цели. Назначается величина “допустимого” снижения первого критерия 
Шаг 2. Решение задачи вида:



Пусть  – оптимальное значение функции цели. Назначается величина “допустимого” снижения второго критерия
– оптимальное значение функции цели. Назначается величина “допустимого” снижения второго критерия 
...
Шаг k. Решение задачи вида:






Пусть  – оптимальное значение функции цели. Назначается величина “допустимого” снижения k -го критерия
– оптимальное значение функции цели. Назначается величина “допустимого” снижения k -го критерия 
...
Шаг М. Решение задачи:


 (22)
(22)



Пусть  – множество решений задачи.
– множество решений задачи.
Шаг М+1. Останов.  – множество решений задачи (2) методом последовательных уступок.
– множество решений задачи (2) методом последовательных уступок.
Замечание 1. Отметим, что при 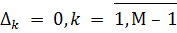 принцип оптимальности, основанный на методе последовательных уступок, становится лексикографическим принципом.
принцип оптимальности, основанный на методе последовательных уступок, становится лексикографическим принципом.
Отметим, что решения, получаемые методом последовательных уступок, не всегда являются эффективными. Однако справедлива следующая теорема.
Теорема 1. Если  – единственная (с точностью до эквивалентности) точка, получаемая методом последовательных уступок, то она эффективна.
– единственная (с точностью до эквивалентности) точка, получаемая методом последовательных уступок, то она эффективна.
|
|
|
Доказательство. Предположим противное: вектор  не является оптимальной по Парето точкой. Тогда существует вектор
не является оптимальной по Парето точкой. Тогда существует вектор  такой, что:
такой, что:

и существует 
Тогда Y удовлетворяет всем ограничениям задачи, получаемой на шаге М алгоритма 2, причем  , т.е.
, т.е.  также является решением задачи (22). Получили противоречие с единственностью
также является решением задачи (22). Получили противоречие с единственностью  . Теорема доказана.
. Теорема доказана.
Несмотря на то, что не всегда решения, получаемые методом последовательных уступок, являются Парето-оптимальными, в некоторых случаях среди решений существует хотя бы одна эффективная точка. В связи с этим справедлива следующая теорема.
Теорема 2. Если  – множество замкнутое и ограниченное, а все частные критерии
– множество замкнутое и ограниченное, а все частные критерии  – непрерывные функции, то среди решений, получаемых методом последовательных уступок, существует, по крайней мере, одна эффективная стратегия.
– непрерывные функции, то среди решений, получаемых методом последовательных уступок, существует, по крайней мере, одна эффективная стратегия.
Доказательство. При выполнении условий теоремы множество  решений задачи (22) оказывается непустым, замкнутым и ограниченным. Следовательно существует точка
решений задачи (22) оказывается непустым, замкнутым и ограниченным. Следовательно существует точка  , в которой функция
, в которой функция

достигает наибольшего на  значения.
значения.
Полученная стратегия  является эффективной в исходной задаче (доказать самостоятельно). Теорема доказана.
является эффективной в исходной задаче (доказать самостоятельно). Теорема доказана.
Таким образом, согласно теореме 2, для получения эффективной точки среди решений, формируемых методом последовательных уступок, достаточно решить задачу:




То есть понятие эффективной стратегии позволило уточнить вычислительную процедуру отыскания оптимальных стратегий методом последовательных уступок. С другой стороны, методом последовательных уступок позволяет указать характеристическое свойство эффективных стратегий. Для этого докажем теорему 3, воспользовавшись результатами леммы 1.
Лемма 1. Если 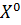 – эффективная стратегия, то она является решением задачи:
– эффективная стратегия, то она является решением задачи:



для любого 
Теорема 3. Для любой эффективной стратегии 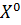 существуют такие числа
существуют такие числа  , что эту стратегию можно получить методом последовательных уступок, т.е.при
, что эту стратегию можно получить методом последовательных уступок, т.е.при  (
( ) вектор
) вектор 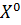 является единственным (с точностью до эквивалентности) решением, получаемым алгоритмом 2.
является единственным (с точностью до эквивалентности) решением, получаемым алгоритмом 2.
Доказательство. Сформируем величины  по следующим правилам:
по следующим правилам:
1)  где
где 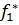 – оптимальное значение функции цели задачи:
– оптимальное значение функции цели задачи:


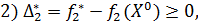 где
где  – оптимальное значение функции цели задачи:
– оптимальное значение функции цели задачи:
|
|
|



М – 1)  где
где  – оптимальное значение функции цели задачи:
– оптимальное значение функции цели задачи:


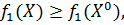


Тогда задача (22) М-го шага алгоритма 2 примет вид:



так что ее решениями, согласно лемме 1, являются лишь 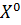 и эквивалентные ей точки.
и эквивалентные ей точки.
Теорема доказана.
Теорема 3 показывает, что метод последовательных уступок, так же как и метод взвешенных сумм, может быть использован для построения множества Парето задачи векторной максимизации (2).
Приведем несколько примеров.
Пример 1. Решить задачу векторной оптимизации методом последовательных уступок:


Ω = 
если 
Решение. Допустимое множество задачи изображено на рисунке 12.
1. Так как критерий  важнее
важнее  , то, согласно алгоритму 2, на первом шаге решаем следующую задачу:
, то, согласно алгоритму 2, на первом шаге решаем следующую задачу:

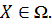 (23)
(23)
Решением частной задачи (23) является отрезок АВ, где А = (0,3), В = (1,3), оптимальное значение функции цели 
2. На втором шаге алгоритма решаем задачу:


что равносильно задаче:

 (24)
(24)
Допустимым множеством (24) является четырехугольник ABCD, решением задачи (24) – отрезок BC, где B = (1, 3), C = (1,6; 2,4).
Так как в исходной задаче два критерия, то отрезок BC является решением исходной ЗВМ. Однако следует заметить, что оптимальной по Парето является только точка В.

Пример 2. Решить задачу векторной оптимизации методом последовательных уступок, если  и
и  = 0,2,
= 0,2,  = 0,3:
= 0,3:



Ω = 
Решение. Допустимым множеством задачи, изображенным на рисунке 13, является многоугольник ABCDEF, где А = (0,0), B = (0,2), C = (2; 3,5), D = (3,5; 2,5), E = (4; 1,5), F = (3,0).
Решаем задачу: 
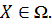 (25)
(25)
Решением (25) является точка D = (3,5; 2,5), а 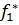 = 2,5 + 3,5 = 6.
= 2,5 + 3,5 = 6.

1. Решаем задачу:


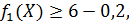
то есть

 (26)
(26)

Допустимое множество задачи (26) изображено на рисунке 14.
Решением (26) является точка  , являющаяся пересечением прямых:
, являющаяся пересечением прямых:
 и
и  .
.
Решая соответствующую систему, получаем:  = (2,9; 2,9);
= (2,9; 2,9);  = 2,9.
= 2,9.
2. Решение задачи:




то есть:


 (27)
(27)


Допустимое множество задачи (27) изображено на рисунке 15.
Решением (27), а следовательно, и исходной ЗВМ, является точка  пересечения прямых:
пересечения прямых:  и
и 

Упражнения к § 7
№ 1. Решить задачу векторной оптимизации методом последовательных уступок:
|
|
|
1) 



если  и
и 

2) 



если  и
и 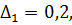

№ 2. Пользуясь результатами теоремы 3, для эффективной точки  найти такие величины уступок
найти такие величины уступок  , что
, что  является решением ЗВМ методом последовательных уступок:
является решением ЗВМ методом последовательных уступок:
1) 


если  = (1/2; 1/2);
= (1/2; 1/2);
2) 


если  = (1/3; 2/3);
= (1/3; 2/3);
3) 


если  = (2; 1);
= (2; 1);
4) 


если  = (3, 5; 0, 5);
= (3, 5; 0, 5);
5) 

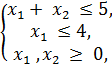
если  = (2; 3);
= (2; 3);
6) 
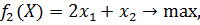

если  = (2; 2).
= (2; 2).
Целевое программирование
Рассмотрим допустимое множество 
 – критерии оценки векторов множества
– критерии оценки векторов множества  . Будем предполагать, что в критериальном пространстве
. Будем предполагать, что в критериальном пространстве  задано непустое, выпуклое множество
задано непустое, выпуклое множество  такое, что любые векторы
такое, что любые векторы  из множества
из множества
 ,
,
где 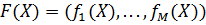 , являются “хорошими” для лица, принимающего решения.
, являются “хорошими” для лица, принимающего решения.
Множество  задается посредством введения ограничений на принимаемые критериями значения, которые можно разделить на следующие группы:
задается посредством введения ограничений на принимаемые критериями значения, которые можно разделить на следующие группы:
1) 
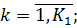
2) 

3) 

4) 

Если пересечение множеств  достижимого множества
достижимого множества  в пространстве критериев
в пространстве критериев  не является пустым (
не является пустым ( ), то решением задачи выбора являются точки
), то решением задачи выбора являются точки  . Однако, как правило,
. Однако, как правило,  ). Тогда множество
). Тогда множество  называется утопическим множеством в пространстве критериев, а
называется утопическим множеством в пространстве критериев, а  – утопическим множеством в пространстве решений. В этом случае ставится задача отыскания таких точек
– утопическим множеством в пространстве решений. В этом случае ставится задача отыскания таких точек  допустимого множества
допустимого множества 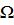 , критериальные векторы
, критериальные векторы  которых наиболее близки в смысле введенной меры близости к утопическому множеству. Такая задача носит название задачи целевого программирования (ЦП). В качестве методов целевого программирования решения задачи векторной максимизации рассмотрим метод идеальной точки и метод сведения к архимедовой задаче.
которых наиболее близки в смысле введенной меры близости к утопическому множеству. Такая задача носит название задачи целевого программирования (ЦП). В качестве методов целевого программирования решения задачи векторной максимизации рассмотрим метод идеальной точки и метод сведения к архимедовой задаче.
Метод идеальной точки
Рассмотрим ЗВМ (2) и точку  где
где  – оптимальное значение функции цели в k -й частной задаче:
– оптимальное значение функции цели в k -й частной задаче:


Как правило, точка  , называемая идеальной точкой, не принадлежит достижимому множеству в пространстве критериев и тем самым образует утопическое множество. Тогда ставится задача отыскания таких векторов
, называемая идеальной точкой, не принадлежит достижимому множеству в пространстве критериев и тем самым образует утопическое множество. Тогда ставится задача отыскания таких векторов  , критериальные векторы которых наиболее близки в смысле введенного расстояния
, критериальные векторы которых наиболее близки в смысле введенного расстояния  ,то есть решается задача:
,то есть решается задача:

 (28)
(28)
В качестве функции  может быть выбрана одна из следующих метрик в пространстве
может быть выбрана одна из следующих метрик в пространстве  :
:
1)  ;
;
2)  где
где 
В силу свойств функции расстояния, получаемые в ходе решения задачи (28) точки являются Парето–оптимальными.
Метод сведения к архимедовой задаче
Рассмотрим задачу целевого программирования, в которой задаваемые экспертом ограничения на критерии разделены на следующие группы:
1)  (X) ≥
(X) ≥  ,
, 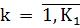 ;
;
2)  (X) =
(X) =  ,
, 
3)  ≤
≤  (X) ≤
(X) ≤  ,
,  .
.
Введем в рассмотрение переменные величины  ,
, 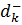 , называемые переменными нежелательных отклонений критериев. Архимедова задача заключается в отыскании таких векторов
, называемые переменными нежелательных отклонений критериев. Архимедова задача заключается в отыскании таких векторов  , для которых взвешенная сумма нежелательных отклонений принимает наименьшее значение:
, для которых взвешенная сумма нежелательных отклонений принимает наименьшее значение:
|
|
|

ΩA  (29)
(29)
где  ,
,  - задаваемые экспертом веса, характеризующие важность нежелательных отклонений.
- задаваемые экспертом веса, характеризующие важность нежелательных отклонений.
Архимедова задача (29) может быть решена методами линейного программирования. При этом отметим, что целевые ограничения в задаче (29) являются нежесткими в том смысле, что они не ограничивают допустимую область Ω в пространстве решений. В действительности они пополняют область допустимых решений, переводя Ω в пространство большей размерности и создавая таким образом расширенную (или архимедову) область допустимых решений для задачи ЦП.
Для задач целевого программирования вводится следующее определение эффективной точки.
Определение 1. Пусть  – вектор нежелательных отклонений, соответствующий точке
– вектор нежелательных отклонений, соответствующий точке  . Будем говорить, что точка
. Будем говорить, что точка  ЦП-эффективна (в смысле минимизации отклонений), если не существует другой точки
ЦП-эффективна (в смысле минимизации отклонений), если не существует другой точки  , которой соответствует вектор
, которой соответствует вектор  , удовлетворяющий условиям:
, удовлетворяющий условиям:  ,
,  .
.
Так как целевая функция в задаче (29) представляет собой взвешенную сумму нежелательных отклонений, то решением архимедовой задачи является ЦП-эффективная точка.
Для определения ЦП-эффективного множества можно использовать аппарат векторной оптимизации, образуя минимизируемые критерии из переменных нежелательных отклонений:


( .
.
В случае, если критерии в задаче ЦП упорядочены по важности ( возможно использование методов лексикографической оптимизации. В этом случае задача целевого программирования решается методом лексикографического ЦП:
возможно использование методов лексикографической оптимизации. В этом случае задача целевого программирования решается методом лексикографического ЦП:
 ,
,


 ,
,

 .
.
Если при этом критерии ЗВМ упорядочены нестрого, и некоторый уровень приоритета включает отклонение нескольких критериев (целей), то один из возможных способов постановки задачи – минимизация максимального отклонения для критериев одного уровня. В этом случае вводится минимаксная переменная λ и критерий на рассматриваемом уровне приобретает вид:
 .
.
Составляя -задачу на рассматриваемом уровне приоритета, необходимо выписать столько дополнительных ограничений, сколько имеется переменных отклонения на данном уровне (см. пример 2).
Рассмотрим некоторые примеры.
Пример 1. Построить архимедову задачу и найти ее решения, если
 =
=  ,
,  =
=  ,
,
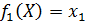 ,
,
 ,
,

где  = 8,
= 8,  = 7.
= 7.
Решение. Допустимое множество исходной задачи изображено на рисунке 16 и представляет собой многоугольник OABC, где O = (0,0), A = (0,4), B = (4,6), C = (10,0).

Утопическим множеством в пространстве критериев является точка  =
=  . Достижимое множество
. Достижимое множество  , а также утопическое множество
, а также утопическое множество  представлены на рисунке 17. Архимедова задача имеет вид:
представлены на рисунке 17. Архимедова задача имеет вид:
 +
+  +
+  +
+ 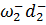 → min,
→ min,


При  ,
,  целевая функция архимедовой задачи имеет вид:
целевая функция архимедовой задачи имеет вид:

 .
.
Рассмотрим линии уровня архимедовой целевой функции в координатах ( , для чего координатную плоскость разобьем на следующие области:
, для чего координатную плоскость разобьем на следующие области:
1) 
2) 
3) 
4) 
Рассмотрим область, определяемую условием 1). В этой области

Линии уровня функции цели:

При этом 

Тогда


то есть:

Тогда:

Соответствующий участок линии уровня изображен на рисунке 18 при  и на рисунке 19 при
и на рисунке 19 при  .
.
Аналогично в области, определяемой условиями 2), получаем 
Линии уровня в этом случае задаются следующим уравнением:
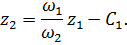


Рассматривая оставшиеся два случая, получаем, что при  линии уровня архимедовой целевой
линии уровня архимедовой целевой  функции – это горизонтально сжатые ромбы с центром в точке
функции – это горизонтально сжатые ромбы с центром в точке  (рис.19). Следовательно, критериальный вектор
(рис.19). Следовательно, критериальный вектор  – это решение архимедовой задачи ЦП, так как
– это решение архимедовой задачи ЦП, так как  – это общая точка; точка наименьшего ромба с центром в точке
– это общая точка; точка наименьшего ромба с центром в точке  и достижимого множества
и достижимого множества  в пространстве критериев, как показано на рисунке 18. Соответственная точка в пространстве решений имеет вид:
в пространстве критериев, как показано на рисунке 18. Соответственная точка в пространстве решений имеет вид: 
При  ромбы сжаты по вертикали (рис.19), а точка
ромбы сжаты по вертикали (рис.19), а точка  – решение архимедовой задачи ЦП в критериальном пространстве, которой соответствует точка
– решение архимедовой задачи ЦП в критериальном пространстве, которой соответствует точка  в пространстве решений.
в пространстве решений.
Пример 2. Сформулировать ЦП-задачу минимизации максимальных отклонений, если  для задачи:
для задачи:
 ;
; 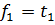 ;
;
 ;
;
 ;
;
 ;
;
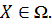
Решение. Лексикографическая формулировка задачи ЦП имеет вид:
 ,
,

Упражнения к §8
№ 1. Для задачи ЦП построить утопическое множество в пространстве решений; утопическое множество в пространстве критериев; архимедову задачу:
1) 


где 

2) 


где 

№ 2. Рассмотрим задачу ЦП вида:



утопическое множество которой определяется:
1) двумя критериями, ограниченными по диапазону;
2) одним критерием с ограничением больше или равно, а другим – ограничением-равенством;
3) двумя критериями с ограничениями больше или равно.
Считая, что  построить линии уровня архимедовой задачи в критериальном пространстве для каждого из перечисленных случаев.
построить линии уровня архимедовой задачи в критериальном пространстве для каждого из перечисленных случаев.
№ 3. Для задачи ЦП с приоритетом целей  построить и решить лексикографическую задачу ЦП:
построить и решить лексикографическую задачу ЦП:
1) 

 ,
,
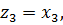


2) 



3) 


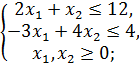
4) 


№ 4. Рассмотрите задачу: 






Считая, что  сформулировать лексикографическую задачу минимизации максимального отклонения на первом и втором уровнях приоритета.
сформулировать лексикографическую задачу минимизации максимального отклонения на первом и втором уровнях приоритета.
№ 5. Задачи векторной оптимизации упражнения № 5 к параграфу 5 решить методом идеальной точки.
|
|
|


