 |
5.2. Методы синтеза механизмов
|
|
|
|
5. 2. Методы синтеза механизмов
с высшими кинематическими парами
Для воспроизведения требуемого движения при малом числе звеньев применяются механизмы с высшими кинематическими парами. Их достоинство в том, что они преобразуют движение теоретически точно, чего механизмы с низшими парами выполнить не могут. В зубчатом зацеплении непрерывное движение выходного звена обеспечивается путем последовательного взаимодействия нескольких пар сопряженных поверхностей. Основным параметром зубчатых передач является передаточное отношение. Наличие высшей кинематической пары вносит существенные особенности в методы синтеза механизма.
5. 3. Основная теорема зацепления
При зацеплении в плоскости основная теорема зацепления устанавливает связь между геометрией сопряженных профилей и их относительным движением, т. е. для передачи вращения с заданным отношением угловых скоростей необходимо, чтобы общая нормаль к сопряженным профилям в точке их касания делила межцентровое расстояние на части, обратно пропорциональные угловым скоростям, и проходила через полюс зацепления:
(5. 7)
5. 4. Эвольвента и ее свойства
|
| Рис. 5. 4 |
Если по окружности без скольжения перекатывать прямую (рис. 5. 4), то каждая точка прямой очертит на плоскости, жестко связанной с этой окружностью, кривую, которая называется эвольвентой. Окружность, по которой происходит прокатывание прямой, называется основной.
Для расчета зубчатых
передач следует отметить наиболее важные свойства эвольвенты:
1) нормаль АВ к эвольвенте касательна к основной окружности радиуса rb;
|
|
|
2) в пределе rb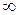 
эвольвента превращается в прямую линию;
3) внутри основной окружности точек эвольвенты нет.
5. 5. Линия зацепления и угол зацепления
Рис. 5. 5
| Согласно основной теореме зацепления общая нормаль к профилям в точке их касания должна проходить через полюс зацепления. Следовательно, касание профилей должно происходить в такой точке К, в которой обе касательные к основным окружностям (радиусы rb1 и rb2)вытянутся в одну прямую линию АВ, являющуюся общей нормалью к профилям. Эта линия называется линией зацепления (рис. 5. 5). |
Угол α , образованный линией зацепления с общей касательной t-t к начальным окружностям (радиусы rω 1 и rω 2), называется углом зацепления.
5. 6. Проектирование цилиндрической зубчатой передачи
Кинематическая связь между ротором двигателя и входным звеном исполнительного механизма обычно осуществляется с помощью зубчатых ме-ханизмов.
В большинстве случаев числа зубьев колес цилиндрической зубчатой передачи (например, z1иz2) заданы в качестве исходных. В некоторых передачах задается только z1и передаточное число u12 или отношение i12. В этом случае число зубьев колеса z2 определяют по формуле:
, (5. 8)
а полученное значение округляют до ближайшего целого числа.
Кроме чисел зубьев заданным является и модуль зацепления m, мм (значение модуля в ряде заданий выбрано условно, т. е. без учета действующих нагрузок и схемы привода).
Процесс проектирования зубчатой передачи состоит в определении таких значений ее основных параметров, которые наилучшим образом удовлетворяют предъявляемым к передаче прочностным, кинематическим, геометрическим и экономическим требованиям.
В курсовой работе (проекте) предусматривается геометрический расчет – выбор основных геометрических параметров, определение размеров колес и проверка качественных показателей для нулевого и неравносмещенного зацеплений.
|
|
|
|
|
|
