Главная | Обратная связь | Поможем написать вашу работу!

5.10. Построение активной части линии зацепления и

5. 10. Построение активной части линии зацепления и

рабочих участков профилей зубьев обоих колес

Активная часть линии зацепления – это отрезок СD теоретической линии зацепления NN, расположенный между точками пересечения ее с окружностями вершин колес 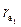и 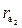(рис. 5. 10). Если ведущим является первое колесо и оно вращается по ходу часовой стрелки, то в точке D начинается зацепление, а в точке С оно заканчивается.

Рабочие участки профилей зубьев – это такие участки, которые участвуют в зацеплении. Учитывая, что в точке D начинается зацепление (см. рис. 5. 10), т. е. в ней контактируют крайняя точка а головки зуба первого (ведущего) колеса и низшая точка ножки зуба второго (ведомого) колеса, радиусом О₂D сделаем засечку на исходном профиле зуба (который сопрягается с построенным) большего колеса ( ). Эта засечка и определит положение низшей рабочей точки

зуба второго колеса. Делая засечку радиусом О₁С на профиле зуба первого колеса (с'), определим аналогичную точку для него. Рабочие участки зубьев колес штрихуются с внутренней части зуба (ас' и вd'). Ширина зоны штриховки составляет 2 – 3 мм.

Т а б л и ц а 5. 2

Значения коэффициента ψ для неравносмещенного внешнего зацепления при 2 ≥ U₁₂ ≥ 1

z₁
ψ	0, 127	0, 145	0, 16	0, 175	0, 19	0, 202	0, 215	0, 227	0, 239	0, 25	0, 257	0, 265	0, 272	0, 278

Т а б л и ц а 5. 3

Значения коэффициентов х₁ и х₂ для неравносмещенного внешнего зацепления при 2 ≥ U₁₂ ≥ 1

z₂	z₁
z₂

	х₁	x₂	х₁	x₂	х₁	x₂	х₁	x₂	х₁	x₂	х₁	x₂	х₁	x₂
	0, 684	0, 684
	0, 723	0, 658	0, 720	0, 720
	0, 756	0, 639	0, 756	0, 699	0, 755	0, 755
	0, 792	0, 617	0, 793	0, 676	0, 793	0, 731	0, 782	0, 782
	0, 814	0, 609	0, 830	0, 652	0, 831	0, 707	0, 821	0, 758	0, 812	0, 812
	0, 849	0, 588	0, 860	0, 636	0, 866	0, 686	0, 861	0, 732	0, 850	0, 787	0, 839	0, 839
	0, 871	0, 579	0, 888	0, 622	0, 893	0, 673	0, 892	0, 715	0, 884	0, 761	0, 872	0, 820	0, 865	0, 865
	0, 898	0, 566	0, 915	0, 639	0, 926	0, 654	0, 925	0, 696	0, 924	0, 742	0, 913	0, 793	0, 898	0, 845
	0, 916	0, 561	0, 937	0, 601	0, 948	0, 645	0, 951	0, 683	6, 950	0, 729	0, 946	0, 774	0, 934	0, 822
	0, 937	0, 552	0, 959	0, 592	0, 976	0, 632	0, 976	0, 672	0, 984	0, 708	0, 979	0, 755	0, 966	0, 804

О к о н ч а н и е т а б л. 5. 3


	х₁	x₂	х₁	x₂	х₁	x₂	х₁	x₂	х₁	x₂	х₁	x₂	х₁	x₂
	0, 958	0, 543	0, 980	0, 583	0, 997	0, 624	1, 000	0, 662	1, 007	0, 700	1, 010	0, 737	1, 000	0, 784
	0, 976	0, 537	0, 997	0, 578	1, 018	0, 615	1, 023	0, 651	1, 031	0, 689	1, 038	0, 723	1, 033	0, 764
	0, 994	0, 532	1, 017	0, 571	1, 038	0, 608	1, 045	0, 641	1, 051	0, 681	1, 055	0, 718	1, 060	0, 750
	1, 011	0, 528	1, 038	0, 562	1, 056	0, 602	1, 065	0, 634	1, 075	0, 669	1, 084	0, 701	1, 081	0, 741
	1, 026	0, 525	1, 054	0, 559	1, 076	0, 594	1, 082	0, 629	1, 094	0, 662	1, 101	0, 696	1, 105	0, 720
	1, 041	0, 522	1, 071	0, 554	1, 093	0, 589	1, 102	0, 622	1, 114	0, 655	1, 121	0, 689	1, 127	0, 720
	1, 059	0, 516	1, 088	0, 550	1, 110	0, 584	1, 122	0, 614	1, 131	0, 650	1, 145	0, 678	1, 149	0, 719
35	1, 072	0, 515	1, 102	0, 547	1, 127	0, 580	1, 140	0, 608	1, 154	0, 639	1, 163	0, 672	1, 170	0, 702
	1, 088	0, 511	1, 117	0, 545	1, 141	0, 578	1, 157	0, 603	1, 172	0, 634	1, 180	0, 667	1, 188	0, 696
			1, 131	0, 542	1, 159	0, 573	1, 171	0, 601	1, 187	0, 631	1, 200	0, 659	1, 206	0, 690
			1, 145	0, 540	1, 173	0, 570	1, 186	0, 599	1, 204	0, 626	1, 218	0, 653	1, 223	0, 685
					1, 187	0, 538	1, 201	0, 595	1, 222	0, 622	1, 232	0, 651	1, 241	0, 680
					1, 201	0, 567	1, 218	0, 591	1, 233	0, 621	1, 249	0, 647	1, 260	0, 673
							1, 231	0, 589	1, 250	0, 616	1, 265	0, 643	1, 276	0, 669
							1, 247	0, 586	1, 266	0, 612	1, 279	0, 640	1, 291	0, 665
									1, 279	0, 611	1, 295	0, 636	1, 306	0, 662
									1, 293	0, 609	1, 310	0, 634	1, 321	0, 659
											1, 325	0, 631	1, 336	0, 657
											1, 338	0, 629	1, 350	0, 654
													1, 365	0, 651
													1, 379	0, 649

Т а б л и ц а 5. 4

Значения коэффициентов ψ и х₁ для неравносмещенного внешнего

зацепления при 5 ≥ U₁₂ > 2

z₁
ψ	0, 16	0, 17	0, 18	0, 19	0, 20	0, 21	0, 22	0, 23	0, 24	0, 25	0, 25
х₁	0, 66	0, 73	0, 80	0, 86	0, 92	0, 98	1, 04	1, 10	1, 16	1, 22	1, 27

Т а б л и ц а 5. 5

Значения коэффициента х₂ для неравносмещенного внешнего зацепления

при 5 ≥ U₁₂ > 2

z₂	z₁
z₂
	0, 442	0, 425
	0, 501	0, 486	0, 471	0, 463
	0, 556	0, 542	0, 528	0, 522	0, 518	0, 512	0, 505
	0, 610	0, 596	0, 582	0, 577	0, 575	0, 569	0, 564	0, 560	0, 553
	0, 661	0, 648	0, 635	0, 632	0, 628	0, 624	0, 620	0, 616	0, 611	0, 606	0, 566
	0, 709	0, 696	0, 685	0, 684	0, 682	0, 677	0, 674	0, 671	0, 667	0, 662	0, 623
	0, 754	0, 745	0, 734	0, 732	0, 731	0, 728	0, 727	0, 722	0, 720	0, 716	0, 677
		0, 789	0, 782	0, 780	0, 779	0, 778	0, 777	0, 773	0, 772	0, 769	0, 729
			0, 822	0, 825	0, 826	0, 827	0, 825	0, 823	0, 821	0, 820	0, 778
				0, 866	0, 870	0, 872	0, 874	0, 871	0, 869	0, 868	0, 828
					0, 909	0, 914	0, 917	0, 920	0, 919	0, 916	0, 876
						0, 954	0, 957	0, 961	0, 962	0, 965	0, 924
							0, 998	0, 101	1, 003	1, 008	0, 964
								1, 042	1, 046	1, 048	1, 005
									1, 086	1, 088	1, 045
										1, 129	1, 087
											1, 131

Рис. 5. 10

5. 11. Определение качественных показателей зацепления

К качественным показателям следует отнести такие, которые характеризуют работу зубчатой передачи. В курсовой работе рассмотрим два основных показателя: коэффициент перекрытия ε и коэффициенты относительного скольжения λ ₁ и λ ₂.

Коэффициент перекрытия – это отношение длины дуги зацепления к длине шага по начальным (r_ω₁ и r_ω₂) окружностям колес, он характеризует непрерывность зацепления, а значит, плавность и бесшумность работы передачи.

До того как зацепление вычерчено, коэффициент перекрытия вычисляется по теоретической формуле:

(5. 9)

где α _ω – угол зацепления в других видах передач;

α – угол зацепления в нулевой передаче.

Для нулевого зацепления sin α _ω = sin α = sin 20^о.

Действительный коэффициент перекрытия определяется из чертежа зацепления по формуле:

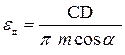, (5. 10)

где СD – действительный участок линии зацепления, мм;

m – модуль зацепления, мм;

α = 20^о.

Определив коэффициенты перекрытия по формулам (6. 3) и (6. 4), сравнить их значения и вычислить относительную ошибку, которая не должна превышать 5 %:

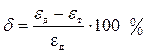. (5. 11)

Во время работы профили зубьев одновременно совершают процесс качения и скольжения. Трение качения мало и в расчетах им пренебрегают, а трение скольжения вызывает износ зубьев. Главным фактором, определяющим износ, является скорость скольжения. Характеризуют влияние скорости скольжения коэффициенты относительного скольжения – λ ₁ и λ ₂ (рис. 5. 11), которые рассчитываются по формулам:

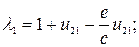(5. 12)

(5. 13)

(5. 14)

(5. 15)

где е – длина теоретической линии зацепления (см. рис. 5. 10, участок АВ), мм, между основаниями перпендикуляров, опущенных из центров О₁ и О₂ на ли-нию NN;

с – расстояние от основания перпендикуляра, проведенного из центра меньшего колеса (z₁) (от точки А) до точки основания перпендикуляра из
центра большего колеса (z₂) (до точки В) через 15 – 30 мм.

Рис. 5. 11

Продолжением перпендикуляра О₁А является линия АМ, а перпендикуляра О₂В – линия ВR, расстояние между которыми равно е. Строить график изменений коэффициентов λ ₁ и λ ₂ рекомендуется на продолжении названных перпендикуляров, откладывая положительные значения над линией ОО, отрицательные – под ней (см. рис. 5. 11). Линиями аб и вг ограничена рабочая зона (по точкам С и D – линии зацепления). Масштаб можно выбрать любой: от М10: 1 до М100: 1. Для удобства построения рекомендуется составить таблицу значений λ ₁ и λ ₂ в зависимости от величин е и с (см. табл. 5. 6).

Таблица 5. 6

Результаты расчета коэффициентов скольжения

NР

е – с

λ ₁

–∞

λ ₂

–∞

Пример определения качественных показателей зацепления.

При е = 120 мм: с = 0; с₁= 16 мм; с₂= 32 мм; с₃= 48 мм; NP = 57 мм; ...,
с = е = 120 мм; при этом е – с = 120 – 16 = 104 мм; 120 – 32 = 88 мм и т. д.

Подставив поученные значения с и (е – с) в формулы (5. 10) и (5. 13), вычислим значения величин λ ₁ и λ _2..

Рекомендации к оформлению курсовой работы изложены в методическом пособии «Анализ и синтез плоских рычажных механизмов. Часть 1» в разделе 1 «Общие положения».

Вопросы для подготовки к защите
второй части курсовой работы (ПРОЕКТА)

1) Задачи синтеза зубчатых механизмов.

2) Виды зубчатых передач.

3) Кривые, очерчивающие профиль зуба.

4) Основные параметры передач (любых).

5) Способы изготовления зубчатых колес.

6) Параметры зубчатых колес, их расчет.

7) Отличия нулевого зацепления от неравносмещенного.

8) Выбор коэффициентов смещения инструмента.

9) Коэффициент перекрытия. Его пределы.

10) Изменение коэффициента перекрытия в зависимости от угла зацепления.

11) Начальная и делительная окружности. Отличие.

12) Теоретический и действительный участок линии зацепления. Границы.

13) Качественные показатели зацепления.

14) Назначение основной окружности.

15) Как найти рабочую часть профиля зуба?

16) Физический смысл коэффициента перекрытия.

Библиографический список

1. Тимофеев Г. А. Теория механизмов и машин: Учебное пособие / Г. А. Тимофеев. М.: Юрайт, 2011. 351 с.

2. Смелягин А. И. Теория механизмов и машин: Учебное пособие / А. И. Смелягин. М.: Инфра-М, 2006. 262 с.

3. Теория механизмов и машин: Учебное пособие / Под ред. М. З. Козловского. М.: Академия, 2008. 558 с.

4. Смелягин А. И. Теория механизмов и машин. Курсовое проектирование: Учебное пособие. – М.: Инфра-М; Новосибирск: Изд-во НГТУ, 2003. – 263 с. – (Серия «Высшее образование»).

5. Артоболевский И. И. Теория механизмов и машин / И. И. Артоболевский. М.: Наука, 1988. 640 с.

Учебное пособие

ВЕЛЬГОДСКАЯ Татьяна Владимировна,

КОВАЛЕВА Нина Васильевна,

ГРИЦ Дмитрий Борисович.

ТЕОРИЯ МЕХАНИЗМОВ И МАШИН

СИНТЕЗ ЗУБЧАТЫХ МЕХАНИЗМОВ

Часть 2

____________________________

Редактор И. Л. Рязанцева

***

Подписано в печать 10. 01. 2023. Формат 60 ´ 84¹/₁₆.

Офсетная печать. Бумага офсетная. Усл. печ. л. 1, 9. Уч. -изд. л. 2, 1.

Тираж 250 экз.

_______________________________

Отпечатано в типографии ООО Издательство «Русь».

Омск, пр. Карла Маркса 41/56, тел/факс: +7(3812)372-442

⇐ Предыдущая 1 2 3 45

Воспользуйтесь поиском по сайту: