5.7. Нулевое зубчатое зацепление

Вычислив размеры элементов зацепления по формулам, приведенным в табл. 5. 1, вычерчивают зацепление. При этом масштаб выбирают в зависи-мости от модуля: если модуль равен 4; 4, 5; 5; 6мм, то масштаб следует принять М4: 1; если модуль равен 7; 8; 9; 10; 11; 12мм – М2: 1.

В нулевом зацеплении делительная и начальная окружности совпадают. Делительная - это такая окружность, для которой модуль стандартный; по этой окружности откладываются шаг зацепления (Р_t) и толщина зуба (S). Начальные - это такие окружности, которые перекатываются одна по другой без скольжения, они характеризуют передачу. Сумма радиусов начальных окружностей составляет межосевое расстояние, а точка касания называется полюсом зацепления (Р).

Порядок вычерчивания зацепления следующий. Из центров О₁ и О₂
(рис. 5. 6), расположенных на расстоянии а_ω друг от друга, провести начальные окружности радиусом r_{ω 1}  и r_{ω 2}, которые касаются друг друга в полюсе Р, через точку Р - касательную ХХ перпендикулярно к прямой О₁О₂, а под углом α = 20^о к касательной ХХ - линию зацепления NN и затем на нее из центров О₁ и О₂ опустить перпендикуляры О₁А и О₂В. Через основания перпендикуляров (А и В) из соответствующих центров провести окружности радиусом r_b1  и r_b2, которые называются основными.

Для построения эвольвент зубьев первого и второго колес отрезки АР и ВР следует разделить на произвольное количество частей, причем части отрезка АР могут быть не равны частям отрезка ВР. На рис. 5. 6 эти отрезки разделены на четыре части: А – 1; 1 – 2; 2 – 3; 3 – P и B – 1; 1 – 2; 2 – 3; 3 – P. Взяв в раствор циркуля длину одной части на участке АР, сделать засечки на основной окруж-ности , начиная от точки А в обе стороны, и получить точки  2', 3', р₁', 4', 5', затем соединить их с центром О₁, чтобы через них точнее провести касательные к основной окружности  Каждая касательная – это прямая NN, занимающая разные положения при перекатывании ее по основной окружности без скольжения.

При пользовании табл. 5. 1 нужно учесть, что h^* = 1; с^*  = 0, 25; α _ω = 20^о; z₂ >  z₁. Индекс «1» принадлежит меньшему колесу (ведущему), «2» – большему
(ведомому).

Т а б л и ц а   5. 1

Формулы для подсчета размеров элементов

зубчатого цилиндрического зацепления

Наименование элемента зацепления	Обозначение	Вид зацепления
		нулевое	неравносмещенное
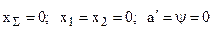
Шаг зацепления по делительной окруж-ности, мм	рt
Радиус делительной окружности, мм	r
Окружная делительная толщина зуба, мм	s
Радиус окружности впадин, мм	rf
Межосевое расстояние, мм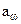
Отклонение межосевого расстояния, мм
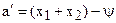
Расстояние между делительными окружностями на линии центров, мм
Радиус начальной окружности, мм	rω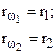
Глубина захвата зубьев, мм	hd
Высота зуба, мм	h
Уменьшение высоты зуба неравносмещенного зацепления, мм
Радиус окружности вершин, мм	ra

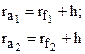
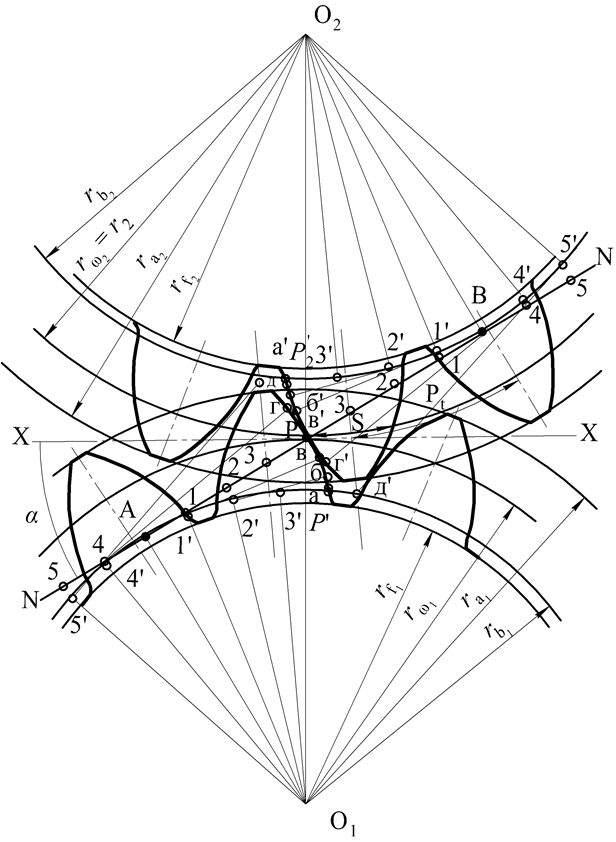
Рис. 5. 6

Так как эвольвента – это кривая, которую описывает точка прямой, перекатываемой по окружности без скольжения, а прямой является линия зацепления NN, то на каждом положении линии зацепления из соответствующих точек касания (1', 2', 3', 4', 5') отложить следующее количество отрезков до полюса: на АР – четыре; на 1'в – три; на 2'б – два; на 3'а – один (точка р₁' находится на основной окружности и является началом эвольвенты); на 4'г– пять; на 5'д – шесть. Точки р₁', а, б, в, Р, г, д соединить плавной кривой. Точно также построить эвольвенту для зуба второго колеса (р₂, а, б, в, Р, г, д). Эвольвента очерчивает участок зуба от основной окружности до окружности вершин. Следует заметить, что радиус окружности впадин (r_f) может быть больше, равен или меньше радиуса основной окружности (r_b), этозависит от числа зубьев колес. Радиус переходной кривой (галтели) ножки зуба колеса принимается равным 0, 4m, мм.

У нулевого зацепления толщина зубьев и шаг обоих колес по делительным окружностям одинаковы, мм: s₁ = s₂ = 0, 5 р_t; р_t  (см. табл. 5. 1).

Чтобы начертить зуб, нужно отложить по делительнымокружностям r₁ и r₂ (от полюса Р) толщину зуба s₁ и s₂ соответственно и, разделив ее пополам, провести через точки О₁ и О₂ осевые линии зуба. Затем с помощью кальки или лекала вычертить вторую половину зуба. Далее по делительной окружности отложить от осевой линии зуба шаг зацепления р_t (в обе стороны), провести осевые линии двух других зубьев и скопировать еще два зуба (см. рис. 5. 6).