Тема 7.2. Методы статистического анализа в задачах моделирования и прогнозирования социально-правовых процессов

Учебные вопросы:

1. Этапы исследования с использованием статистических методов

2. Корреляционный анализ

3. Регрессионный анализ

4. Факторный анализ

5. Кластерный анализ

6. Анализ динамики и прогнозирование социально-правовых процессов

Этапы исследования с использованием статистических методов

В литературе по моделированию и прогнозированию социально-правовых процессов встречаются во многом сходные схемы исследования, направленные на анализ взаимосвязей между различными процессами и явлениями с использованием статистических методов и моделей.

С использованием анонсированных схем можно выделить 6 основных этапов исследования.

Этап 1. Определение цели исследования.

На этом этапе:

- анализируется исследуемая реальная система и объекты, входящие в систему;

- выбирается перечень показателей, характерный для данной системы и описывающий ее состояние;

- оценивается объем исследования, необходимое время и трудозатраты;

- разрабатываются формы для сбора исходной информации;

- осуществляется выбор методов математического описания исследуемой системы, то есть производится выбор среди множества моделей той, которая наилучшим образом (в определенном смысле) соответствует имеющимся в распоряжении исследователя статистическим данным.

Этап 2. Сбор статистических данных и разработка схемы их анализа.

На этом этапе:

- формируется массив данных для ввода в ЭВМ и осуществляется их ввод, а также запись на магнитные носители.

Этап 3. Первичная статистическая обработка данных.

На этом этапе решаются задачи:

- формирование выборки в соответствии с заданными параметрами репрезентативности;

- выявление и анализ резко отличающихся наблюдений с реконструкцией пропущенных данных.

Этап 4. Разработка плана проведения вычислений.

На этом этапе проводится:

- обработка данных с использованием ЭВМ;

- получение исходных зависимостей.

Этап 5. Статистическая проверка значимости и надежности полученных результатов.

Этап 6. Интерпретация полученных результатов.

 

В ходе исследования социально-экономических процессов и явлений, как правило, возникает проблема учета и анализа большого числа показателей. Отсюда возникает необходимость применения в практике исследования социально-экономических процессов методов многомерного статистического анализа.

Многомерный статистический анализ применяется для решения следующих вопросов:

- классификация объектов (кластерный анализ, дискриминантный анализ, распознавание образов и др.);

- снижение размерности исследуемого пространства показателей и отбор из их числа наиболее весомых (факторный анализ, многомерное шкалирование и др.);

- исследование зависимости между анализируемыми признаками (корреляционный анализ, регрессионный анализ, дисперсионный анализ и др.).

Отдельные методы многомерного статистического анализа успешно применяются для обработки статистической информации в сфере борьбы с преступностью, например, при исследовании факторов, влияющих на оперативную обстановку, а также на расстановку сил и средств.

Пример применения методов многомерного статистического анализа:

1) применение метода экстремальной группировки параметров:

- при построении типологии регионов в целях борьбы с преступностью;

- при агрегировании статистической информации и конструирования обобщенных показателей оперативно-служебной деятельности органов внутренних дел;

2) применение факторного анализа:

- при анализе криминологических характеристик контингента освобожденных и др.

На практике для обработки исходного статистического материала все чаще применяется комбинированный подход. В основе комбинированного подхода – использование различных методов и моделей многомерного статистического анализа.

Суть комбинированного подхода заключается в совместном применении различных методов многомерного статистического анализа, например:

- использование факторного анализа позволяет определить набор сравнительно небольшого числа показателей и отобрать из них наиболее информативные;

- проведение кластерного анализа, с учетом результатов, полученных на основе факторного анализа, способствует разработке многомерной типологии изучаемых объектов;

- регрессионный метод позволяет получить математические модели (регрессии на ранее выделенных факторах, на различных показателях, на однородных группах объектов) и исследовать зависимость между различными переменными. Найденные количественные соотношения с использованием регрессионных уравнений дают возможность лучше понимать сущность и особенности исследуемых процессов и явлений.

Примеры применения комбинированного подхода:

- при исследовании взаимосвязи характеристик преступности и социально-экономических факторов развития городов;

- при изучении влияния различных факторов на автотранспортную аварийность.

 

Корреляционный анализ

Между социально-экономическими процессами и явлениями возможны два вида зависимостей:

- функциональная - имеется однозначное соответствие параметров, характеризующих различные процессы и явления (в социальной среде практически не встречаются);

- стохастическая (вероятностная) - конкретному значению зависимой переменной соответствует набор значений объясняющей переменной. Это связано, прежде всего, с тем, что на зависимую переменную оказывает влияние ряд неучтенных факторов. Кроме того, сказываются ошибки измерения переменных – вследствие случайного разброса значений их значения могут быть указаны лишь с определенной вероятностью.

Примерами случайных явлений, имеющими вероятностную природу и встречающимися в социально-экономической сфере, можно указать следующие:

- число совершенных и раскрытых преступлений за фиксированный отрезок времени (это – случайные величины);

- число дорожно-транспортных происшествий в регионе за определенное время (это также случайная величина) и др.

Для изучения стохастических взаимосвязей существуют специальные методы, в частности, корреляционный анализ.

Корреляция – это соотношение, связь между имеющимися явлениями и процессами.

Корреляционный анализ – это использование в определенной последовательности совокупности статистических методов обработки информации, позволяющее исследовать взаимосвязи между различными признаками.

Задачами корреляционного анализа как метода математической статистики для изучаемых случайных признаков являются:

- установление формы связи между изучаемыми случайными признаками;

- установление направления связи между изучаемыми случайными признаками;

- измерение тесноты этой связи между изучаемыми случайными признаками.

В статистике величина линейной зависимости между двумя признаками измеряется посредством простого (выборочного) коэффициента корреляции.

Величина линейной зависимости одной переменной от нескольких других измеряется коэффициентом множественной корреляции.

Возможно вычисление частного коэффициента корреляции, измеряющего линейную зависимость межу двумя признаками после устранения части линейной зависимости, обусловленной связью этих переменных с другими переменными.

По форме корреляционные связи могут быть:

- линейными (прямолинейными);

- нелинейными (криволинейными).

По направлению корреляционные связи могут быть:

- прямыми (положительными);

- обратными (отрицательными).

 

Коэффициент корреляции может принимать значения:

- при прямой связи – от 0 до +1;

- при обратной связи – от -1 до 0;

- при коэффициентах, близких к нулю, считается, что статистическая линейная связь между признаками отсутствует;

- при абсолютных значениях коэффициентов, меньше 0,3 – связь слабая;

- при значениях 0,3 – 0,5 – связь умеренная;

- при значениях 0,5– 0,7 – связь значительная;

- при значениях 0,7 – 0,9 – связь сильная;

- при значениях коэффициентов больше 0,9 – связь считается сильной;

- при значениях коэффициентов, равных +1 или -1, говорят о наличии функциональной связи (такая ситуация практически не встречается в статистических исследованиях).

Однако такая упрощенная оценка силы связи не всегда корректна, так как степень уверенности в наличии статистической связи зависит от объема исследуемой совокупности.

Чем меньше объем совокупности, тем большим должно быть значение коэффициента корреляции для принятия гипотезы о существовании зависимости между признаками.

С целью количественного измерения степени уверенности в существовании линейной статистической связи между признаками введены понятия:

- уровня значимости коэффициента корреляции;

- пороговое (критическое) значение коэффициента корреляции.

Проверка значимости полученного коэффициента корреляции состоит в сравнении расчетного значения с критическим.

При данном числе измерений и задаваемым уровнем значимости находится критическое значение, которое сравнивается с расчетным.

Если расчетное значение коэффициента корреляции больше критического – связь считается значимой.

Если расчетное значение коэффициента корреляции меньше критического, то связь или отсутствует (такое значение коэффициента корреляции объясняется случайными отклонениями), или выборка мала для ее выявления.

Для определения существования и величины линейной зависимости между двумя переменными X и Y необходимо осуществить две процедуры:

Процедура 1. Графическое отображение точек [(Xi, Yi), i = 1, n на плоскость [XY]. Полученный график называется диаграммой рассеяния, анализ которой позволяет сделать вывод о допустимости предположения о линейной зависимости между перемен­ными. Если такое предположение допустимо, то необходимо выразить в количественном виде величину линейной связи. Для этого исполь­зуется выборочный коэффициент корреляции:

 

 

 

Где n - количество измерений, Xi.Yi - i-е значения, X,Y - сред­ние значения, бх, бу - среднеквадратические отклонения перемен­ных X и Y соответственно.

В теории статистического анализа корреляционная связь определяется как линейная зависимость в условиях нормальности распределения анализируемых переменных. Поэтому для корректного применения корреляционных методов необходимо обосновать близость распределения переменных к нормальному и формы связи к линейной. В противном случае необходимо применять более сложные приемы анализа или другие коэффициенты связи.

Достаточно простой в вычислительном отношении способ про­верки нормальности эмпирического распределения состоит в оценке следующего отношения:

Где С - среднее абсолютное отклонение, б - среднеквадратическое отклонение.

Если указанное неравенство выполняется, то можно говорить о нормальности эмпирических распределений и корректности применения коэффициента корреляции как меры линейной статистической связи между переменными.

Однако даже при наличии сильной статистически значимой cвязи между двумя переменными нельзя быть полностью уверенным в причинно-следственной обусловленности, так как могут существовать другие причины (факторы), определяющие их совместную статистическую взаимосвязь. Статистические выводы должны быть всегда обоснованы надежной теоретической концепцией.

В то же время отсутствие статистически значимой связи не говорит об отсутствии причинно-следственных отношений, а заставляет искать другие пути и средства ее выявления, если содержательная концепция и практический опыт указывают на ее возможное существование.

3. Регрессионный анализ

Понятия корреляции и регрессии непосредственно связаны между собой. В корреляционном и регрессионном анализе много общих вычислительных приемов. Они используются для выявления причинно-следственных соотношений между явлениями и процессами. Однако, если корреляционный анализ позволяет оценить силу и направление стохастической связи, то регрессионный анализ - еще и форму зависимости.

Регрессия может быть:

А) в зависимости от числа явлений (переменных):

- Простой (регрессия между двумя переменными);

- Множественной (регрессия между зависимой переменной (у) несколькими объясняющими ее переменными (x1, х2,...,хn);

- Линейной (отображается линейной функцией, а между изучае­мыми переменными существуют линейные соотношения);

- Нелинейной (отображается нелинейной функцией, между изучаемыми переменными связь носит нелинейный характер);

В) по характеру связи между включенными в рассмотрение переменными:

- Положительной (увеличение значения объясняющей переменной приводит к увеличению значения зависимой переменной и наоборот);

- Отрицательной (с увеличением значения объясняющей пере­менной значение объясняемой переменной уменьшается);

Г) по типу.

- Непосредственной (в этом случае причина оказывает прямее воздействие на следствие, т.е. Зависимая и объясняющая перемен­ные связаны непосредственно друг с другом);

- Косвенной (объясняющая переменная оказывает опосредован­ное действие через третью или ряд других переменных на зависимую переменную);

- Ложной (нонсенс регрессия) - может возникнуть при поверх­ностной и формальном подходе к исследуемым процессам и явлениям. Примером бессмысленных является регрессия,, устанавливающая связь между уменьшением количества потребляемого алкоголя в нашей стране и уменьшением продажи стирального порошка.

При проведении регрессионного анализа решаются следующие основные задачи:

1. Определение формы зависимости.

2. Определение функции регрессии. Для этого используют ма­тематическое уравнение того или иного типа, позволяющее, во-пер­вых, установить общую тенденцию изменения зависимой перемен­ной, а, во-вторых, вычислить влияние объясняющей переменной (или нескольких переменных) на зависимую переменную.

3. Оценка неизвестных значений зависимой переменной. Полу­ченная математическая зависимость (уравнение регрессии) позволя­ет определять значение зависимой переменной как в пределах ин­тервала заданных значений объясняющих переменных, так и за его пределами. В последнем случае регрессионный анализ выступает в качестве полезного инструмента при прогнозировании изменений со­циально-экономических процессов и явлений (при условии сохране­ния существующих тенденций и взаимосвязей). Обычно длина вре­менного отрезка, на который осуществляется прогнозирование, вы­бирается не более половины интервала времени, на котором прове­дены наблюдения исходных показателей. Можно осуществить как пас­сивный прогноз, решая задачу экстраполяции, так и активный, ведя рассуждения по известной схеме "если.... То" и подставляя раз­личные значения в одну или несколько объясняющих переменных рег­рессии.

Для построения регрессии используется специальный метод, получивший название метода наименьших квадратов. Этот метод име­ет преимущества перед другими методами сглаживания: сравнительно простое математическое определение искомых параметров и хорошее теоретическое обоснование с вероятностной точки зрения.

При выборе модели регрессии одним из существенных требова­ний к ней является обеспечение наибольшей возможной простоты, позволяющей получить решение с достаточной точностью. Поэтому для установления статистических связей вначале, как правило, рассматривают модель из класса линейных функций (как наиболее простейшего ив всех возможных классов функций):

 

Где bi, b2,...,bj - коэффициенты, определяющие влияние независимых переменных xjj на величину yi;ai - свободный член; σi - слу­чайное отклонение, которое отражает влияние неучтенных факторов на зависимую переменную; n - число независимых переменных; N -число наблюдений, причем должно соблюдаться условие (N > n+1).

Линейная модель может описывать весьма широкий класс раз­личных задач. Однако на практике, в частности в социально-эконо­мических системах, подчас затруднительно применение линейных мо­делей из-за больших ошибок аппроксимации. Поэтому нередко ис­пользуются функции нелинейной множественной регрессии, допускаю­щие линеаризацию. К их числу, например, относится производственная функция (степенная функция Кобба-Дугласа), нашедшая при­менение в различных социально-экономических исследованиях. Она имеет вид:

Где b0 - нормировочный множитель, bi...bj - неизвестные коэффи­циенты, εi - случайное отклонение.

Используя натуральные логарифмы, можно преобразовать это уравнение в линейную форму:

Log у* = log b0 + b1log x1 +...+ bjlog xj+log εi.

Полученная модель позволяет использовать стандартные проце­дуры линейной регрессии, описанные выше. Построив модели двух видов (аддитивные и мультипликативные), можно выбрать наилучшие и провести дальнейшие исследования c меньшими ошибками аппроксимации.

Существует хорошо развитая система подбора аппроксимирующих функций - методика группового учета аргументов (МГУА).

О правильности подобранной модели можно судить по результа­там исследования остатков εi являющихся разностями между наблюдаемыми величинами yi и соответствующими прогнозируемыми с помощью регрессионного уравнения величинами уi*. В этом случае для проверки адекватности модели рассчитывается средняя ошибка ап­проксимации:

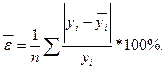
Модель считается адекватной, если I находится в пределах не более 15%.

Особо подчеркнем, что применительно к социально-экономичес­ким системам далеко не всегда выполняются основные условия адекватности классической регрессионной модели.

Не останавливаясь на всех причинах возникающей неадекватности, назовем лишь мультиколлинеарность - самую сложную проблему эффективного применения процедур регрессионного анализа при изучении статистических зависимостей. Под мультиколлинеарностью понимается наличие линейной связи между объясняющими переменными. Это явление:

А) искажает смысл коэффициентов регрессии при их содержательной интерпретации;

Б) снижает точность оценивания (возрастает дисперсия оценок);

В) усиливает чувствительность оценок коэффициентов к выборочным данным (увеличение объема выборки может сильно повлиять на значения оценок).

Существуют различные приемы снижения мультикодлинеарноста. Наиболее доступный способ - устранение одной из двух переменных, если коэффициент корреляции между ними превышает значение, равное по абсолютной величине 0,8. Какую из переменных оставить решают, исходя из содержательных соображений. Затем вновь проводится расчет коэффициентов регрессии.

Использование алгоритма пошаговой регрессии позволяет последовательно включать в модель по одной независимой переменной и анализировать значимость коэффициентов регрессии и мультиколлинеарность переменных. Окончательно в исследуемой зависимости остаются только те переменные, которые обеспечивают необходимую значимость коэффициентов регрессии и минимальное влияние мультиколлинеарности.

Факторный анализ

Анализ функционирования социально-экономических систем сопряжен с необходимостью исследования значительного числа различных показателей. Однако многомерность описания может служить помехой, как при обработке исходных данных, так и при содержательной интерпретации полученных результатов. Построение корреляционных и регрессионных моделей "в лоб", когда число показателей достигает нескольких десятков, порой оказывается затруднительно. Поэтому возникает естественная необходимость в сжатии исходной информации, в замене исходных показателей на такие переменные, которые оказались бы наиболее информативными и отражающими существенные свойства изучаемого процесса. В дальнейшем изложении будем именовать такие переменные факторами.

В настоящее время факторный анализ широко используется при исследовании различных проблем:

- В экономике - для построения обобщенных показателей, для проведения типологии предприятий и агрегирования отраслей;

- В социологии - для классификации социальных объектов и изучения общественного мнения, в том числе для анализа качественных признаков;

- В экономической географии - в целях районирования, моделирования миграционных процессов, типологического исследования городов и др.

Методы факторного анализа широко применяются для исследования проблем, возникающих в сфере борьбы с преступностью.

Факторный анализ позволяет извлечь на поверхность некоторую величину (так называемый фактор), которая всегда стоит за наблюдаемыми величинами, но сама при этом для измерения остается недоступной.

Основная идея факторного анализа заключается в группировке с помощью специальных процедур множества исходных показателей в ограниченное число скрытых факторов. Подчеркнем, что термин "фактор" применяется в специфическом смысле. Если в общенаучном смысле фактором может быть назван любой признак какой-либо системы, то в факторном анализе под этим термином понимают внутрен­ний, скрытый параметр системы, а наблюдаемые признаки лишь косвенно характеризуют тот или иной фактор.

Приведем несколько примеров, иллюстрирующих идею факторного анализа.

В социологических исследованиях при обследовании населения измеряемыми параметрами являются ответы на вопросы анкеты, а факторами, определяющими ответы анкетируемого, - такие неизмеряемые характеристики, как социальный статус, культурный уровень, общественная активность анкетируемого и т.д.

Психологи, проводя свои исследования, фиксируют реакцию че­ловека посредством тех или иных тестов. Факторами, которые определяют реакции испытуемого, являются, например, тренированность, темперамент, математические или художественные способности.

В социологии права факторами могут выступать правовая уста­новка, уровень знания права, причины правонарушения и др.

Для формализации постановки задачи факторного анализа, как правило, делается допущение о линейной связи между измеренными параметрами и факторами. Нелинейные модели пока не получили широкого распространения в силу значительных вычислительных трудностей и сложности в интерпретации результатов в сравнении с линейными моделями. Таким образом, предполагается, что каждый из анализируемых признаков, параметров, характеризирующих тот или иной объект наблюдения, явление и т.п., может быть представлен следующей линейной формой:

Где α, kj - коэффициенты ("факторные нагрузки"), которые необ­ходимо определить; fk - обозначения факторов; uj - "характерный фактор", изменение которого влияет на значение соответствующего параметра XJ.

Для определения общих факторов, и соответствующих факторных нагрузок используется ряд методов. Наиболее широкую известность получили метод главных компонент и центроидный метод. Эти классические модели факторного анализа объединяет одна цель: опреде­лить общие факторы и факторные нагрузки таким образом, чтобы по ведение вычисленных параметров было бы близко к поведению измеренных параметров хj. Различие этих моделей определяется критериями близости.

Существует и другой подход к обработке эмпирических данных, основанный на анализе матрицы, элементами которой являются величины степени близости между измеренными параметрами. Результатом обработки такой матрицы может быть разбиение исходного множества параметров на непересекающиеся подмножества. При этом величины степени близости между параметрами, оказавшимися в одном подмножестве, заметно сильнее, чем между параметрами из разных подмно­жеств. Такой подход в отличие от классических методов факторного анализа позволяет использовать иной путь выявления существенных факторов: вначале осуществляется разбиение параметров на сильно связанные подмножества, а затем для каждого подмножества выделяется свой существенный фактор. Этот метод получил название метода экстремальной группировки параметров.

Факторный анализ имеет в своем арсенале различные методы, решающую роль в выборе которых играют опыт исследователя, ресурсы ЭВМ и имеющееся программное обеспечение. Наиболее простым считается центроидный метод. Для научных исследований при наличии ЭВМ используют метод главных компонент.

Факторный анализ необходим не только для выявления действующих факторов и проведения оценки их значений; его результаты могут быть использованы и для проведения классификации различных объектов. Во многих социально-экономических задачах часто возникает необходимость разбиения исследуемых объектов на однородные группы. Такое разбиение значительно упрощает построение различных математических моделей и проведение дальнейших исследований. При классификации объектов невольно возникает вопрос о том, какие и сколько наблюдаемых признаков необходимо включить в рассмотрение. На первый взгляд, может показаться, что чем больше таких признаков взято, тем точнее и лучше будут классифицированы исследуемые объекты. Однако однородные группы, построенные в пространстве большого числа признаков, могут оказаться неустойчивыми и плохо объяснимыми. В этом случае предварительно выявленные факторы с учетом значений их весов могут быть использованы для сравнения различных групп объектов и определения степени различия между ними.

Кластерный анализ

В социально-правовых исследованиях нередко возникает необходимость проведения классификации изучаемых объектов и выявления среди множества объектов группы с похожими свойствами. Задачи классификации неоднократно решались как у нас в стране, так и за рубежом при изучении территориальной дифференциации различных условий жизнедеятельности человека. Учет объектовых и территориальных неоднородностей необходим для выработки управленческих решений, для обоснования и принятия различных социально-экономи­ческих программ.

В отечественной научной литературе наиболее широко освещены вопросы территориальной дифференциации применительно к городским и сельским населенным пунктам. В зарубежных исследованиях большое внимание уделено проблемам типологии городов и населенных пунктов, районирования, типологического анализа в исследовании мировой экономики и международных отношений.

Перечень работ, посвященных социально-экономическим вопросам, достаточно обширен. Однако исследований, проведенных с использованием типологического подхода и посвященных проблемам совершенствования органов внутренних дел, сравнительно немного. Упомянем лишь некоторые направления исследований.

На основе методов экстремальной группировки параметров и автоматической классификации осуществлена многомерная типология регионов Российской Федерации в целях борьбы с преступностью.

С использованием методов кластерного анализа проводилась социально-экономическая типология 67 городов России и были выделены качественно однородные группы, что позволило разработать математические модели взаимосвязей характеристик преступности и социально-экономических факторов развития городов.

Необходимость классификации по сочетанию ряда признаков можно проиллюстрировать на примере исследования, посвященного проблеме безопасности дорожного движения, в котором была осуществлена необходимая типология крупных городов.

Простейшая классификация городов может быть осуществлена, например, по числу проживающих жителей или числу зарегистрированных транспортных средств, по числу дорожно-транспортных происшествий, имевших место за фиксированный отрезок времени, и т.д. Однако такой упрощенный подход неприемлем, поскольку объектом изучения явилась безопасность дорожного движения в крупных городах - сложных целостных системах.

В общем виде задача кластерного анализа заключается в следующем. Используя данные, отражающие различные характеристики объектов, необходимо провести их разбиение на m однородных непе­ресекающихся подмножеств (кластеров). При этом каждый объект Ai должен принадлежать только одному кластеру. Объекты, входящие в один и тот же кластер, должны быть сходными, а принадлежащие разным кластерам - разнородными.

Процедура кластерного анализа осуществляется ступенчато. Вначале объединяются в один кластер два наиболее "близко расположенных" объекта. Число исходных объектов уменьшается и становится равным n-1 (при этом один кластер содержит два объекта). Повторяя процесс объединения, можно последовательно получить множество кластеров, состоящее из n-2, n-З кластеров и т.д.

Проведение описанных процедур с использованием методов факторного и кластерного анализов позволяет, во-первых, "сжать" пространство исходных показателей и выявить существенные внутренние характеристики-факторы, а во-вторых, проводить исследование на однородных группах изучаемых объектов, образованных по итогам многомерной классификации.

⇐ Предыдущая29303132333435363738Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: