Функции, используемые при прогнозировании временных рядов Линейная, Экспоненциальная, Степенная, Гиперболическая

Допустим, что аналитическая форма функции тренда выражается уравнением прямой линии Y(t) - а + b*t. Коэффициенты а и b из условия минимизации суммы квадратов отклонений определяются сле­дующими соотношениями:

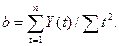
При выборе вида функций из нескольких возможных предпочте­ние следует отдать той, у которой ошибка S меньше.

Важное место в задачах прогнозирования временных рядов отводится методу экспоненциального сглаживания, которое осуществляется с помощью экспоненциально-взвешенных скользящих средних. При этом имеется возможность учитывать с большим весом наблюдения, имеющие большую информационную ценность, в частности, можно задавать большие веса более поздним наблюдениям по сравнению с ранними наблюдениями. Такая возможность придает гибкость в описании динамического ряда.

К простейшим эмпирическим методам относятся метод сглажива­ния уровней путем укрупнения интервалов и метод скользящих средних. Достоинством их являются простота и наглядность. К недостаткам, в частности метода скользящих средних, следует отнести искажение вида тенденции для коротких рядов динамики, трудность обоснования выбора интервала сглаживания, потерю нескольких уровней ряда и др.

Метод укрупнения интервалов является одним из самых простых эмпирических способов. Суть его состоит в том, что в результате анализа ряда выбирается соответствующий укрупненный интервал, в пределах которого складываются показатели уровней имеющегося ряда, в результате чего получается новый выровненный ряд.

К простейшим экстраполяционным методам относятся методы средней геометрической, средней арифметической и среднего абсолютного прироста. Их целесообразно использовать, если уровни ряда последовательно увеличиваются иди уменьшаются. Для рядов с сильно колеблющимися уровнями вычисление средних теряет смысл.

Рассмотрим простейшие характеристики динамического ряда:

- Разность ∆Y - Y(t)-Y(t-1) называется абсолютным приростом;

- Отношение Т - Y(T)/Y(t-1) - темпом роста;

- отношение ∆Т - (Y(t)-Y(t-1))'/Y(t-1) - темпом прироста.

Прогнозирование может осуществляться с помощью средних ха­рактеристик динамического ряда, в частности:

- средней геометрической Y(t+1) = Y(t)*K1,

Где K1=

- средней арифметической Y(t+1) = Y(t)*K2,

Где К2 = 1/(n-1)*

- среднего абсолютного прироста Y(t+1) - Y(t)+∆Y,где ∆Y = (Y(t)-Y(l))/(t-l).

 

Тема 7.4. «Статистические гипотезы.»

Учебные вопросы:

1.Статистические гипотезы.

2.Критерии проверки статистических гипотез.

3.Ошики первого и второго рода при проверке статистических гипотез.

4.Проверка гипотезы о нормальном распределении ген. совокупности.

Статистические гипотезы.

Проверка статистических гипотез тесно связана с теорией оценивания параметров. В естествознании, технике, экономике для выяснения того или иного случайного факта часто прибегают к высказыванию гипотез, которые можно проверить статистически, т. е. опираясь на результаты наблюдений в случайной выборке. Под статистическими подразумеваются такие гипотезы, которые относятся или к виду, или к отдельным параметрам распределения случайной величины. Например, статистической является гипотеза о том, что распределение производительности труда рабочих, выполняющих одинаковую работу в одинаковых условиях, имеет нормальный закон распределения. Статистической будет также гипотеза о том, что средние размеры деталей, производимые на однотипных, параллельно работающих станках, не различаются.

 

Пусть в (статистическом) эксперименте доступна наблюдению случайная величина X, распределение которой неизвестно полностью или частично. Тогда любое утверждение, касающееся называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:

§ Статистическая гипотеза, однозначно определяющая распределение , то есть , где какой-то конкретный закон, называется простой.

§ Статистическая гипотеза, утверждающая принадлежность распределения к некоторому семейству распределений, то есть вида , где 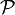- семейство распределений, называется сложной.

На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу H ₀. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза H ₁, называемая конкурирующей или альтернативной.

Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу.

В большинстве случаев статистические критерии основаны на случайной выборке фиксированного объема из распределения . В последовательном анализе выборка формируется в ходе самого эксперимента и потому ее объем является случайной величиной (см. Последовательный статистический критерий).

Пример

Пусть дана независимая выборка из нормального распределения, где μ — неизвестный параметр. Тогда , где μ₀ — фиксированная константа, является простой гипотезой, а конкурирующая с ней — сложной.

 

⇐ Предыдущая29303132333435363738Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: