 |
Вредоносное программное обеспечение
|
|
|
|
Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и анти-шпионскими программами.
Поиск в компьютерных базах данных
При поиске в базе данных, к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако, это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек, которые используемый алгоритм расценил как «a».
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т. п.
|
|
|
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как террориста) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т. д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т. п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении.
Проверка гипотезы.
Статистическая гипотеза называется простой, если она однозначно определяет распределение случайной величины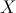 
, в противном случае гипотеза называется сложной. Например, простой гипотезой является предположение о том, что случайная величина 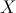распределена по нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Если высказывается предположение, что случайная величина 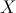имеет нормальное распределение с дисперсией, равной единице, а математическое ожидание — число из отрезка 
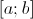, то это сложная гипотеза. Другим примером сложной гипотезы является предположение о том, что непрерывная случайная величина 
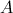с вероятностью 
принимает значение из интервала 
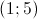, в этом случае распределение случайной величины 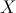может быть любым из класса непрерывных распределений.
|
|
|
Часто распределение величины 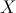известно, и по выборке наблюдений необходимо проверить предположения о значении параметров этого распределения. Такие гипотезы называются параметрическими.
Проверяемая гипотеза называется нулевой и обозначается 
. Наряду с гипотезой рассматривают одну из альтернативных (конкурирующих) гипотез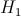 
. Например, если проверяется гипотеза о равенстве параметра 
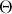некоторому заданному значению 
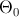, то есть 
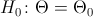, то в качестве альтернативной гипотезы можно рассмотреть одну из следующих гипотез: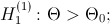 
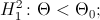
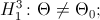
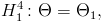где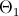 
— заданное значение, 
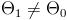. Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.
Правило, по которому принимается решение принять или отклонить гипотезу , называется критерием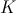 
. Так как решение принимается на основе выборки наблюдений случайной величины 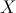, необходимо выбрать подходящую статистику, называемую в этом случае статистикой 
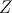критерия 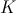. При проверке простой параметрической гипотезы 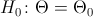в качестве статистики критерия выбирают ту же статистику, что и для оценки параметра .
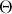Проверка статистической гипотезы основывается на принципе, в соответствии с которым маловероятные события считаются невозможными, а события, имеющие большую вероятность, — достоверными; Этот принцип можно реализовать следующим образом. Перед анализом выборки фиксируется некоторая малая вероятность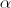 
, называемая уровнем значимости. Пусть 
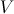— множество значений статистики 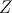, а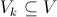 
— такое подмножество, что при условии истинности гипотезы вероятность попадания статистики критерия в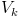 
равна 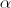, то есть 
.
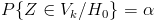Обозначим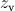 
выборочное значение статистики 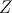, вычисленное по выборке наблюдений. Критерий формулируется так: отклонить гипотезу , если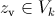 
; принять гипотезу , если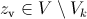 
. Критерий, основанный на использовании заранее заданного уровня значимости, называют критерием значимости. Множество 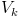всех значений статистики критерия 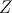, при которых принимается решение отклонить гипотезу , называется критической областью; область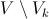 
называется областью принятия гипотезы .
|
|
|
Уровень значимости 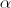определяет размер критической области 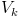. Положение критической области на множестве значений статистики 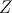зависит от формулировки альтернативной гипотезы 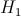. Например, если проверяется гипотеза 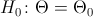, а альтернативная гипотеза формулируется как 
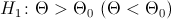, то критическая область размещается на правом (левом) "хвосте" распределения статистики 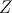, т. е. имеет вид неравенства 
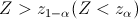, где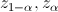 
— значения статистики 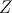, которые принимаются с вероятностями соответственно 
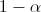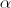и при условии, что верна гипотеза . В этом случае критерий называется односторонним (соответственно правосторонним и левосторонним). Если альтернативная гипотеза формулируется как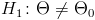 
, то критическая область размещается на обоих "хвостах" распределения 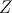, то есть определяется совокупностью неравенств 
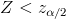и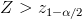 
в этом случае критерий называется двухсторонним.
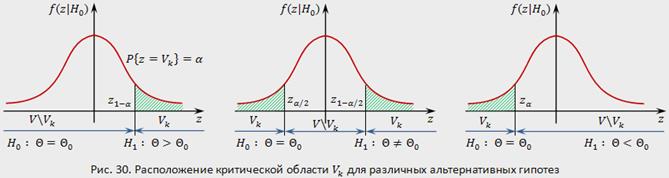
Расположение критической области 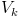для различных альтернативных гипотез показано на рис. 30, где 
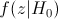— плотность распределения статистики 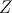критерия при условии, что верна гипотеза , 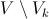— область принятия гипотезы, 
.
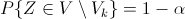Проверку параметрической статистической гипотезы с помощью критерия значимости можно разбить на этапы:
1) сформулировать проверяемую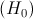 
и альтернативную 
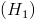гипотезы;
2) назначить уровень значимости ;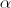
3) выбрать статистику 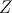критерия для проверки гипотезы ;
4) определить выборочное распределение статистики 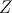при условии, что верна гипотеза ;
5) в зависимости от формулировки альтернативной гипотезы определить критическую область 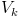одним из неравенств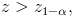 
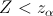или совокупностью неравенств 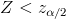и ;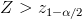
6) получить выборку наблюдений и вычислить выборочные значения 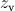статистики критерия;
7) принять статистическое решение: если 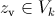, то отклонить гипотезу как не согласующуюся с результатами наблюдений; если 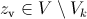, то принять гипотезу , т. е. считать, что гипотеза не противоречит результатам наблюдений.
Обычно при выполнении пп. 4-7 используют статистику с нормальным распределением, статистику Стьюдента, Фишера.
|
|
|
Пример 1. По паспортным данным автомобильного двигателя расход топлива на 100 км пробега составляет 10 л. В результате изменения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки проводятся испытания 25 случайно отобранных автомобилей с модернизированным двигателем, причем выборочное среднее расходов топлива на 100 км пробега по результатам испытаний составило 9,3 л. Предположим, что выборка расходов топлива получена из нормально распределенной генеральной совокупности со средним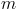 
и дисперсией 
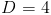л². Используя критерий значимости, проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
Решение. Проверим гипотезу о среднем 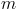нормально распределенной генеральной совокупности. Проверку проведем по этапам:
1) проверяемая гипотеза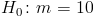 
; альтернативная гипотеза 
;
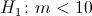2) уровень значимости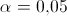 
;
3) в качестве статистики критерия используем статистику математического ожидания — выборочное среднее;
4) так как выборка получена из нормально распределенной генеральной совокупности, выборочное среднее также имеет нормальное распределение с дисперсией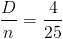 
. При условии, что верна гипотеза , математическое ожидание этого распределения равно 10. Нормированная статистика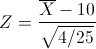 
имеет нормальное распределение;
5) альтернативная гипотеза 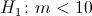предполагает уменьшение расхода топлива, следовательно, нужно использовать односторонний критерий. Критическая область определяется неравенством 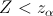. По прил. 5 находим 
;
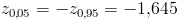б) выборочное значение нормированной статистики критерия
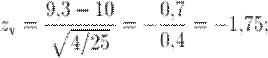
7) статистическое решение: так как выборочное значение статистики критерия принадлежит критической области, гипотеза отклоняется: следует считать, что изменение конструкции двигателя привело к уменьшению расхода топлива. Границу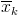 
критической области для исходной статистики 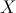критерия можно получить из соотношения 
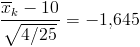, откуда 
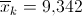, т. е. критическая область для статистики 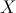определяется неравенством 
.
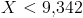Решение, принимаемое на основе критерия значимости, может быть ошибочным. Пусть выборочное значение статистики критерия попадает в критическую область, и гипотеза , отклоняется в соответствии с критерием. Если, тем не менее, гипотеза верна, то принимаемое решение неверно. Ошибка, совершаемая при отклонении правильной гипотезы if о, называется ошибкой первого рода. Вероятность ошибки первого рода равна вероятности попадания статистики критерия в критическую область при условии, что верна гипотеза , т. е. равна уровню значимости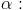 
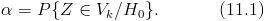
Ошибка второго рода происходит тогда, когда гипотеза принимается, но в действительности верна гипотеза 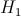. Вероятность 
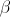ошибки второго рода вычисляется по формуле
|
|
|
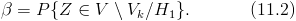
Пример 2. В условиях примера 1 предположим, что наряду с гипотезой 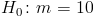л рассматривается альтернативная гипотеза 
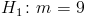л. В качестве статистики критерия снова возьмем выборочное среднее 
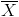. Предположим, что критическая область задана неравенством 
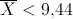л. Найти вероятности ошибок первого и второго рода для критерия с такой критической областью.
Решение. Найдем вероятность ошибки первого рода. Статистика 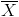критерия при условии, что верна гипотеза 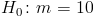л, имеет нормальное распределение с математическим ожиданием, равным 10, и дисперсией, равной 
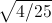. Используя прил. 5, по формуле (11.1) находим
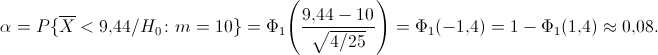Это означает, что принятый критерий классифицирует примерно 8% автомобилей, имеющих расход 10 л на 100 км пробега, как автомобили, имеющие меньший расход топлива. При условии, что верна гипотеза 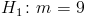л, статистика 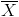имеет нормальное распределение с математическим ожиданием, равным 9, и дисперсией, равной 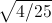. Вероятность ошибки второго рода найдем по формуле (11.2):
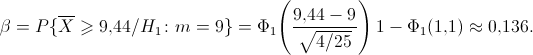
Следовательно, в соответствии с принятым критерием 13,6% автомобилей, имеющих расход топлива 9 л на 100 км пробега, классифицируются как автомобили, имеющие расход топлива 10 л.
Вопросы для самоконтроля:
1. Относительные величины распределения
2. Относительные величины интенсивности
3. Анализ вариационных рядов
4. Понятие статистических взаимосвязей и причинности
5. Измерение связей между качественными признаками
6. Парная линейная корреляция
7. Иные способы установления взаимосвязей
8. Понятие статистического анализа
9. Характер, функции, методы статистического анализа
10. Понятие связи явлений и ее виды.
11. Статистические методы выявления связей между двумя признаками социально-правовых явлений.
12. Виды информации и их характеристика.
13. Этапы статистического анализа.
14. Закон больших чисел и его роль в исследовании социально-правовых явлений.
15. Основные задачи анализа данных уголовно-правовой статистики.
16. Основные направления автоматизированной системы обработки данных правовой статистики. Статистический анализ-основа изучения преступности.
17. Анализ оценка деятельности правоохранительных органов.
18. Анализ показаний гражданско-правовой статистики. Роль статистики в оценке деятельности судов по рассмотрению гражданских дел.
Рекомендуемая литература:
основная: [1,2];
дополнительная:[1, 2, 4].
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Основная
1. Правовая статистика: учебник под ред. В.С. Лялина, А.В. Симоненко. – М.: ЮНИТИ-ДАНА, 2010.-255с.
2. Правовая статистика: учебник учебник под ред. С.Я.Казанцева, С.Я. Лебедева, С.М. Иншакова – М.: ЮНИТИ-ДАНА: закон и право, 2012.-271с.
Дополнительная:
1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высшая школа, 2004.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. - М.:Высшая школа, 2004.
3. Решение математических задач средствами Excel: Практикум/ В.Я. Гельман. – СПб.: Питер, 2003. – 237с.
4. Кремер Н.Ш. Теория вероятностей и математическая статистика: учебник.- М.: ЮНИТИ-ДАНА, 2007. 551с.
5. Статистика: учебник / под ред. И.И. Елисеевой. – М.: Высшее образование, 2008.-566 с
6. Материалы официального сайта Федеральной службы государственной статистики http://www.gks.ru/
Нормативные правовые акты*
|
|
|
