 |
Сопряжение комплексных чисел.
|
|
|
|
ДЕЛИМОСТЬ ЦЕЛЫХ ЧИСЕЛ
Полагаем, что в произвольном подмножестве натуральных чисел всегда есть наименьшее.
Определение. Пусть a, bÎZ. Если существует qÎZ, что a = bq, то b делит a, или a делится на b, обозначаем b|a.
Простейшие свойства делимости:
1) Если a|b, b|c Þ a|c. Если a делит b и b делит c, то a делит c.
2) Если a,b,с и с не равно 0, то a делит b тогда и только тогда, когда ac делит bc, т. е. a|b; c¹0 Û ac|bc, a, b, cÎZ.
3) d|ai; i=1,…,n,x1,…,xnÎZ Þ d|a1 x1 +…+an xn.
4) a|b; b|a Þ a =±b.
Доказательство всех свойств однообразно: используется только определение делимости. Докажем:
4) a = bq и b = aq1 Þ a = aqq1 Þ a(qq1 – 1) = 0 Þ qq1 = 1, т. к. a¹0 Þ q = ±1.
Теорема (о делении с остатком).
Для любых a, bÎZ; b ¹ 0 существует единственная пара q, rÎZ такая, что a = bq+r, 0£ r<|b|.
Доказательство: Рассмотрим множество M = {a – bq, qÎZ}. Очевидно, что M∩{N, 0}¹Ø.
В любом таком множестве $ наименьшее r. Очевидно, что |b|>r ≥0.
Докажем единственность.
Пусть ещё a = bq1 + r1. Тогда вычитанием из первого второе получим
0 = b(q – q1) + r – r1. Отсюда следует, что r – r1 кратно b, но |r – r1|<|b|.
Следовательно, r – r1 = 0, а поэтому и q – q1 = 0.
ПОСТРОЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ.
Уравнение x^2+1=0 не имеет решения в области действительных чисел. Построение комплексных чисел попутно решает задачу о расширении множества действительных чисел до такого множества, чтобы уравнение x^2+1=0 имело решение.
В качестве исходного материала для построения комплексных чисел возьмём множество точек плоскости. Будем их обозначать z1, z2,…, zn. Если на плоскости выбрана Декартова система координат, то между точками на плоскости и множеством пар чисел (a, b), где a и bR, можно установить взаимно однозначное соответствие, т.е.
|
|
|
z =(def) (a, b), где =(def) – равно по определению.
Введём операции сложения и умножения точек плоскости.
Определение 1. Под суммой точек z1=(a, b) и z2=(c, d) будем понимать точку z = z1+z2 (a+c, b+d).
Определение 2. Под произведением точек z1=(a, b) и z2=(c, d) будем понимать точку z = z1z2 =(def) (ac–bd, ad+bc)
Теорема 1.
1) z1+z2=z2+z1 — коммутативность сложения;
2) (z1+z2)+z3= z1+(z2+z3) — ассоциативность сложения;
3) z1z2= z2z1 — коммутативность умножения;
4) (z1z2)z3= z1(z2z3) — ассоциативность умножения;
5) (z1+z2)z3 = z1z3+z2z3 — дистрибутивность умножения относительно сложения.
Для любых z1, z2, z3.
Доказательство утверждений 1) – 5) сводится к подсчёту правой и левой частей и проверке их равенства. Докажем, например, 3):
z1z2 = (ac–bd, ad+bc) = (ca–db, cb+da) = z2z1 Þ z1z2= z2z1.
Введённые операции сложения и умножения обладают теми же свойствами, что и числа.
Определение 3. Под разностью точек z1=(a, b) и z2=(c, d) будем понимать точку z = (x, y) такую, что z2+ z = z1, т.е.
z2+z = z1 Û  Þ
Þ 
z1–z2 = (a – c, b – d).
Определение 4. Пусть z1 = (a, b), z2 = (c, d), z2 (0, 0).
Частным двух точек z1 и z2 называют точку z = (x, y) такую, что z2z = z1, т.е.
 Þ
Þ  Þ
Þ
x =  ; y =
; y =  .
.
Точка с координатами (0, 0) играет роль нуля. Роль единицы играет точка с координатами (1, 0). Противоположной точке z1 = (a, b) будет точка z2 = (–a, –b).
Определение 5. Два комплексных числа равны, если равны их мнимые и действительные части (следует из геометрической интерпретации комплексных чисел).
Два комплексных числа называют сопряжёнными, если их действительные части равны, а мнимые — противоположны (сопряжённое к z обозначаем через).
Теорема 2.
Справедливы следующие соотношения:
1)  =
=  +
+  ;
;
2)  =
=  –
–  ;
;
3)  =
= 
 ;
;
4)  =
=  .
.
Доказательство.
Доказательство 1) – 4) однообразно и сводится к подсчёту левой и правой частей и их сравнению. Например: z1=a+bi, z2=c+di. Докажем
1)  =
=  +
+  . По определению
. По определению  = a-bi;
= a-bi;  =c-di и
=c-di и  = (a+c)–(bi+di),
= (a+c)–(bi+di),  +
+  = (a–bi)+(c–di) = (a+c)–(bi+di).
= (a–bi)+(c–di) = (a+c)–(bi+di).
Значит  =
=  +
+  .
.
СОПРЯЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ.
Пусть z = a+bi, тогда:
a = Re z — действительная часть комплексного числа,
|
|
|
b = Im z — мнимая часть комплексного числа.
Множество точек плоскости может служить геометрическим изображением комплексных чисел.
Определение 5. Два комплексных числа равны, если равны их мнимые и действительные части (следует из геометрической интерпретации комплексных чисел).
Два комплексных числа называют сопряжёнными, если их действительные части равны, а мнимые — противоположны (сопряжённое к z обозначаем через  ).
).
Упражнение 1. Сумма и произведение двух комплексных чисел z и  (сопряжённых) — действительное число.
(сопряжённых) — действительное число.
Теорема 2.
Справедливы следующие соотношения:
1)  =
=  +
+  ;
;
2)  =
=  –
–  ;
;
3)  =
= 
 ;
;
4)  =
= 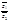 .
.
Доказательство.
Доказательство 1) – 4) однообразно и сводится к подсчёту левой и правой частей и их сравнению. Например: z1=a+bi, z2=c+di. Докажем
1)  =
=  +
+  . По определению
. По определению
 = a-bi;
= a-bi;  =c-di и
=c-di и
 = (a+c)–(bi+di),
= (a+c)–(bi+di),
 +
+  = (a–bi)+(c–di) = (a+c)–(bi+di).
= (a–bi)+(c–di) = (a+c)–(bi+di).
Значит  =
=  +
+  .
.
|
|
|


